Sinn gesucht, Unsinn gefunden

Im Zufallsmuster der Badezimmerkacheln erkennen wir Gesichter. Das Wolkenbild formt sich zu einem Hund. Zwölf von 150 Frauen wählten beim Autokauf einen Ford; unter gleich vielen Männern trafen nur sechs diese Entscheidung. So kommen wir vorschnell zur Auffassung, dass Frauen die Automarke Ford bevorzugen.

Das sind Beispiele dafür, wie Phantasie und Spekulation fast gewohnheitsmäßig über unsere Erfahrung und unser Wissen hinausgreifen. Das ist die unvermeidliche Sinnsuche unseres Wahrnehmungs- und Denkapparats.

Manch ein übersensibler Mensch braucht nur ein paar schwer erklärliche Umstände, sonderbare Riten oder befremdliche Symbole und schon vermeint er die Anzeichen einer Verschwörung zu erkennen. Besonders zwingend wird ein solcher Verdacht, wenn sich in den Beobachtungen mathematische Strukturen ausmachen lassen.

Für den Hochsensiblen kann das kein Zufall sein. Einfache und möglichst geheimnisvolle Erklärungen müssen her. Dann kann er sich seinen esoterischen und verschwörungstheoretischen Gedanken  hingeben und sich genüsslich so manchen Schauer über den Rücken laufen lassen.

Dabei steckt oft nicht mehr als Zufall dahinter, oder Spielerei, oder Wichtigtuerei, oder ein ähnlich harmloser Anlass. Sinn gesucht – Unsinn gefunden!

Ich greife ein Thema der Zahlenmystiker auf. Die folgende Miniatur ist meiner Problemsammlung „Querbeet“ entnommen. Zweck der Problemsammlung ist zwar die freudvolle Beschäftigung mit Mathematik. Andererseits zeigt diese Miniatur Fallstricke der überbordenden Sinnsuche auf und findet so ihren Platz im Hoppla!-Blog.

Zahlenmystik um die Fünf

Für mich begann es mit dem Film „V wie Vendetta“ (2006). Der Held nennt sich V, nach der Nummer der Zelle, in der er eingekerkert war: Fünf. Es ist ein beliebtes Spiel unter Kinogängern, herauszufinden, wo überall in dem Film ein V oder die Zahl Fünf erscheint: bei der Zeigerstellung der Uhr, den Schnitten des Degens, dem Feuerwerk, einem Bild an der Wand, auf den Tasten der Jukebox.

Die Fünf ist von alters her ein Symbol der belebten Natur. Die Fünfzähligkeit zeichnet die Rosengewächse aus. Schneiden Sie einmal einen Apfel quer durch und schauen Sie sich das Kerngehäuse an. Weitere Beispiele sind die fünf Finger unserer Hand und der fünfarmige Seestern.

Dem regelmäßigen Sternfünfeck, dem Pentagramm, wurden bereits in der Antike magische Kräfte zugeschrieben. Heute sieht man es oft auf zwei seiner Spitzen gestellt. Beim Drudenfuß, er soll bis in unsere Tage hinein der Abwehr böser Geister dienen, weist eine Spitze zur Erde. Hier entdecken wir das V schon wieder.

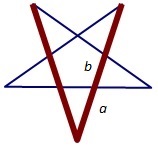
Die Spitzen des Pentagramms bilden ein regelmäßiges Fünfeck, ein Pentagon. Das Zentrum des Pentagramms ist ebenfalls von einem Pentagon umgeben. Ein Pentagon entsteht beispielsweise beim Knüpfen eines einfachen Knotens (Überhandknoten) mit einem Streifen Papier.

Im Pentagramm ist alles goldener Schnitt. Genauer: Zu jeder Strecke (oder Teilstrecke) lässt sich im Pentagramm eine weitere Strecke finden, die zu ihr im Verhältnis des goldenen Schnittes steht. Zur Erinnerung: Eine Strecke ist im goldenen Schnitt geteilt, wenn sich die Gesamtstrecke zur größeren Teilstrecke verhält wie die größere Teilstrecke zu kleineren.

Im obigen Pentagramm habe ich mit a und b die Längen von Streckenabschnitten bezeichnet. Eine Strecke von Spitze zu Spitze hat die Länge 2a + b. Tatsächlich gelten die Gleichungen des goldenen Schnittes, nämlich (2a+b)/(a+b) = (a+b)/a = a/b.

Das Streckenverhältnis des goldenen Schnittes wird zuweilen mit dem griechischen Buchstaben ɸ (Phi) bezeichnet: ɸ = a/b. ɸ ist Lösung der Gleichung ɸ² – ɸ -1 = 0 und hat den Wert 1,61803398874989…

Der Wikipedia entnehme ich diese Deutung des Pentagramms (15.04.2019):  „Pythagoras kannte es als Symbol für Gesundheit. Ihn interessierte daran besonders der mathematische Aspekt des Goldenen Schnitts. Da man es in einem Zug zeichnen kann und am Schluss wieder zum Anfang gelangt, galt es auch als Zeichen für den Kreislauf des Lebens. Abraxas, Gott der Gnostiker, wurde ebenfalls durch ein Pentagramm symbolisiert, weil er fünf Urkräfte in sich vereint.“

Wem das zu wenig Grusel ist, der möge sich an die auf die Spitze gestellte Version mit dem eingezeichneten gehörnten Ziegenkopf halten (Baphomet). Dann sieht er das Pentagramm als Symbol von Geheimgesellschaften und Satanismus. Davor kann er sich dann so richtig fürchten. (Er könnte das folgenlos aber auch sein lassen.)

Der goldene Schnitt wird vom Menschen als besonders harmonisches Streckenverhältnis empfunden. „Die göttliche Proportion … ist der goldene Schnitt… So lässt sich vielleicht die Vorliebe für fünfeckige Strukturen in der gotischen Kunst vor allem in den Verstrebungen der Rosetten der Kathedralen erklären“ (Eco, Umberto: Die Geschichte der Schönheit. Hanser, München, Wien 2004, S. 66 ff.).

Damit sind wir unversehens vom Kino über Mathematik und Magie zur Architektur und zu den schönen Dingen gekommen.

Von da aus mache ich nun einen kühnen Sprung hinein in die Populationsbiologie. Wie viele Kaninchenpaare kann ein Kaninchenpaar im Laufe der Zeit erzeugen? Diese Kaninchenaufgabe hat Leonardo von Pisa, genannt Fibonacci, im Jahre 1202 gestellt.

Aus dem Lehrbuch des Fibonacci: „Das Weibchen eines jeden Kaninchenpaares gebiert von Vollendung des zweiten Lebensmonats an allmonatlich ein neues Kaninchenpaar.“ Es ist die Zahl der Kaninchenpaare im Laufe der Monate zu berechnen unter der Voraussetzung, dass anfangs nur ein Kaninchenpaar vorhanden ist und dass die Kaninchen nicht sterben.

Die Zahlenfolge für die Anzahl der Kaninchenpaare ist 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … Das sind die Fibonacci-Zahlen. Und so lautet das Bildungsgesetz dieser Zahlen: Ab der Zahl 2 ist jede Zahl die Summe ihrer beiden Vorgänger.

Wir bilden nun die Quotienten je zweier aufeinander folgender Fibonacci-Zahlen, und zwar teilen wir die größere der beiden durch die kleinere. Diese Werte streben gegen einen Grenzwert, nämlich gegen die Zahl ɸ des goldenen Schnittes. Und damit sind wir wieder beim Pentagramm, der Zahl Fünf und bei „V wie Vendetta“.

Und was ist der tiefere Sinn des Ganzen? Es gibt ihn nicht. Da ist nichts Mystisches, keine unerklärliche Magie – nur Spiel.

V ist ein sehr einfaches Symbol. Es ist kein Wunder, dass es uns hin und wieder begegnet. Denselben Effekt ruft das „Gesetz der kleinen Zahlen“ hervor (Underwood Dudley: Die Macht der Zahl. 1999): Eine kleine Zahl wie die Fünf erscheint immer wieder einmal. Auch die einfachen Relationen des Pentagramms und dass wir diese in der Fibonacci-Folge wiederfinden, ist nichts Besonderes. Einfaches passiert oft.

Dazu kommt, dass die „Sinnsuche unseres Wahrnehmungsapparats“ vor kleineren Manipulationen nicht zurückschreckt, wie oben bei der leichten Drehung des Pentagramms hin zum Drudenfuß. Auch wird manch „wundersamer“ Fund in der Bedeutung gern überbewertet. Dem Standardwerk zur europäischen Baukunst entnehme ich beispielsweise die Bemerkung : „Der Goldene Schnitt … wird in der Kunst weit seltener angewendet als allg. angenommen wird“ (Koch, Wilfried: Baustilkunde. Bertelsmann Lexikon Verlag, Gütersloh 2000).

Aber was sagen Sie dazu: Das Symbol V hat den Morsecode „…-“, „didididaaa“. Da kommt Ihnen etwas in den Sinn? Musik? Eine Symphonie? Von Beethoven? – Richtig: Es ist die Fünfte.

Spekulation in der Wissenschaft

Ohne Spekulation gibt es keinen Wissenszuwachs. Von esoterischen Umtrieben und von der Pseudowissenschaft unterscheidet sich die Wissenschaft dadurch, dass neue Ideen und Theorien unerbittlich auf innere Konsistenz und auf  Übereinstimmung mit den Fakten geprüft werden.

Beispielsweise war das Weltsystem des Kopernikus zunächst nur eine schöne Spekulation. Das Weltsystem wurde später durch Gelileo durch Beobachtungen und Erfahrung angereichert und so zu Wissenschaft.

Was aber, wenn neue Beobachtungen und Fakten ausbleiben? Die Frage nach dem Sinn des Ganzen verlässt uns ja nicht. Er lässt die Wissenschaftler nach immer schöneren Theorien suchen, nach Theorien, die zwar keine neue Erkenntnis liefern, die aber die  alte Erkenntnis in immer eleganteren Formulierungen zusammenfasst.

Dann droht der Wissenschaft dieselbe Gefahr wie der Zahlenmystik: Sie könnte sich in reiner Spekulation und in bloß illusionärem Denken ergehen. Beispielsweise sieht Sabine Hossenfelder keinen großen Unterschied zwischen dem Glauben, die Natur sei schön und dem Glauben, Gott sei gütig (Spektrum der Wissenschaft 11/2018, S. 21).

Sie sagt: „Ohne empirische Daten könnten mathematische Konsistenz und Ästhetik zu den einzigen Lotsen auf der Suche nach neuen Naturgesetzen werden. Und manchen Physikern würden diese Kriterien möglicherweise bereits genügen, um eine hinreichend ausgearbeitete Theorie für wahr zu erklären.“

Abgrenzung

(Ergänzung vom 18.04.2019)

Wie lässt sich Sinn vom Unsinn scheiden? Woran erkennen wir die nützlichen Vorstellungen und das hilfreiche Wissen? Was zeichnet die fruchtbaren Theorien aus und hebt sie von reiner Spekulation ab?

Nach Karl Raimund Popper müssen Hypothesen, die unser Wissen erweitern, an der Erfahrung scheitern können. Sie müssen prinzipiell falsifizierbar sein. Dieses Kriterium dient ihm zur Abgrenzung wissenschaftlicher Theorien von der Metaphysik.

Es sind also die Fakten und die Überprüfung unserer Vorstellungen und Theorien anhand dieser Fakten, die den Wissensfortschritt ausmachen.

Obwohl Sabine Hossenfelder genau dieses Fehlen von Erfahrung und Fakten den neuen physikalischen Theorien als Manko anlastet, schreibt sie auf Seite 9 ihres Buches „Das hässliche Universum“: „Was ich jedoch lerne, ist, dass Karl Poppers Idee, wissenschaftliche Theorien müssten so gebaut sein, dass sie falsifizierbar sind, längst überholt ist. Ich freue mich, das zu  hören, denn es ist eine Philosophie, die in der Wissenschaft sowieso niemand gebrauchen konnte[…] Eine Idee zu falsifizieren ist nämlich so gut wie nie möglich“.

Diese Geringschätzung des Abgrenzungskriteriums geht meines Erachtens auf eine übertrieben strenge Auffassung von Falsifizierbarkeit und Falsifikation zurück. Karl Raimund Popper zeigt im 9. Abschnitt seiner Logik der Forschung, dass Vorsicht geboten ist: „Wer in den empirischen Wissenschaften strenge Beweise verlangt oder strenge Widerlegungen, wird nie durch Erfahrung eines Besseren belehrt werden können.“

Die Falsifizierbarkeit einer Theorie besagt nicht, dass die tatsächliche Falsifizierung eine einfache Sache ist. Von zentraler Bedeutung ist das Abwägen von Theorien in einem sozialen Prozess. Popper: „Widersprechen anerkannte Basissätze einer Theorie, so sind sie nur dann Grundlage für deren Falsifikation, wenn sie gleichzeitig eine falsifizierende Hypothese bewähren.“ (Logik der Forschung, Abschnitt 22)

Die Widerlegung der Theorie der verborgenen Variablen in der Quantenmechanik ist ein lehrreiches Beispiel. Eine Konsequenz dieser Theorie ist die bellsche Ungleichung. Die Verletzung der bellschen Ungleichung lässt sich nur anhand statistischer Daten erkennen. Einen strengen Beweis geben diese natürlich nicht her. Aber die Datenlage ermöglicht es, dass sich die Wissenschaftler auf ein Urteil einigen: Die Theorie der verborgenen Variablen gilt heute als widerlegt.