Bevor Sie meine Provokation mit wütenden Entgegnungen kommentieren, widerspreche ich mir vorauseilend gleich selbst. Die Denksportaufgaben habe ich in Büchern gefunden, die ich für wertvoll halte. Darin sind interessante Problemstellungen zu finden und die vorgeschlagenen Lösungsverfahren sind in technischen und wissenschaftlichen Zusammenhängen von großem Nutzen. Nur sind sie den zu lösenden Aufgaben nicht angemessen. Es wird sozusagen mit Kanonen auf Spatzen geschossen. Und darin liegt ein weiterer Wert dieser Bücher: Sie regen dazu an, nach besseren und einfacheren Lösungen zu suchen nach dem Motto: „Es geht immer noch einfacher.“ Das ist meine Basisheuristik. Mathematik sollte glücklich machen, eine Art Denksport sein. Diese Absicht verfolge ich auch in Klüger irren – Denkfallen vermeiden mit System (2020).
Den Wahnsinn sehe ich dann um die Ecke kommen, wenn die mathematische Beschäftigung zur Routine wird oder auch, wenn prima Konzepte mittels nervtötender Beispiele eingeführt werden. Darum geht es im ersten Teil von „Denksport am Rande des Wahnsinns“. Im zweiten Teil wende ich mich dann dem Unendlichen zu, das ja in der Mathematik sein Zuhause hat und in der Natur praktisch nicht vorkommt. Das hat schon etwas Unheimliches, einen Anflug von Wahnsinn.
Schulmathematik
Vor nunmehr fast zwei Jahrzehnten fiel mir auf, dass meine Kollegen Mathematikkurse für Studienanfänger anboten, in denen sie Schulstoff vermittelten. Sie boten den Schülern also das an, was bei den Adressaten bereits in der Schule keinen nachhaltigen Eindruck hinterlassen hatte: Die meisten der Studienanfänger waren auf ein technisches Studium nicht vorbereitet worden. Ihnen fehlte es an Fertigkeiten im Rechnen und am Verständnis für grundlegende mathematische Sachverhalte.
Das Problem wurde von den üblichen Brückenkursen nicht gelöst. Ich dachte über ein neues Konzept nach, das im Fuldaer Brückenkurs Mathematik (FBΣ) dann auch umgesetzt wurde. Im Zuge der Vorbereitung hatte ich ein ernüchterndes Erlebnis. Ich studierte die Lehrpläne einiger Bundesländer für ihre Gymnasien und fand nirgendwo das Thema vollständige Induktion, mit Ausnahme Bayerns. Aber auch dort rangierte es ganz hinten: „Die Vollständige Induktion [..] sollte nicht zu sehr vertieft werden“.
Dabei ist die vollständige Induktion etwas, das die Leistungsfähigkeit und Schönheit der Mathematik besonderes sinnfällig macht. Den Schülern wird Wichtiges vorenthalten. Stattdessen quält man sie unablässig mit Optimierungsaufgaben, die sich mittels Differentialrechnung nach festem Schema abhandeln lassen. Im nächsten Abschnitt bringe ich Beispiele dafür, wie diese Sekundarstufen-II-Routine Kreativität bremst.
Bleiben wir zunächst bei der vollständigen Induktion. Soweit ich dem Internet entnehmen kann, wird sie auch heute noch an Beispielen eingeführt, die nur zu zeigen scheinen, dass das Werkzeug eigentlich überflüssig ist. Ein gern genommenes Beispiel ist der Beweis dafür, dass die Summe der ersten n natürlichen Zahlen gleich n(n+1)/2 ist.
Induktionsanfang. Die Formel gilt für n = 1, da 1 = 1×2/2 ist.
Induktionsschluss. Die Formel sei für n-1 anstelle von n bereits bewiesen: 1+2+…+(n-1) = (n‑1)n/2. Daraus folgt 1+2+…+(n-1)+n = (n‑1)n/2+n = ((n‑1)n+2n)/2 = (n‑1+2)n/2 = n(n+1)/2. Das ist die Gültigkeit der Formel für die Zahl n. Damit gilt die Formel für alle natürlichen Zahlen. Was zu beweisen war.
Vom Schüler Carl Friedrich Gauß geht die Rede, dass er seinen Lehrer verblüffte, als er sehr rasch die Zahlen von 1 bis 100 zusammengezählt hatte. Seine Überlegungen könnten diese gewesen sein: Ich denke mir die Zahlen in aufsteigender Folge hingeschrieben, darunter schreibe ich dieselbe Folge noch einmal, diesmal aber in umgekehrter Reihenfolge. Nun stehen immer zwei Zahlen untereinander, die zusammengezählt den Wert 101 ergeben, und das 100- mal. Also habe ich die Summe 10100. Da jede Zahl zweimal vorkommt, muss ich das Ganze noch halbieren und ich komme auf das Ergebnis 5050. Vielleicht hat der kleine Gauß es etwas anders gemacht. Auf so etwas wie die vollständige Induktion ist er sicherlich nicht verfallen.
Noch absurder ist es, wenn man mittels vollständiger Induktion beweist, dass jede natürliche Zahl plus ihr Quadrat eine gerade Zahl ist. Dabei sieht man sofort, dass n+n2 = n(n+1) gerade ist, einfach weil einer der beiden Faktoren gerade sein muss.
So ist gezeigt, wie man Schülern mit schlechten Beispielen den Einstieg in die höhere Mathematik verleiden kann. Aber auch dem bereits Begeisterten kann man die Mathematik noch vergällen. Dazu genügt es, die Kreativität zu lähmen, indem man immer dasselbe Standardschema zur Lösungsfindung empfiehlt.
Übrigens gibt es auch schöne Formeln, denen man nicht sofort ansieht, dass sie gelten müssen. Zum Einstieg in die vollständige Induktion eignet sich das folgende Beispiel: Beweise, dass das Quadrat der Summe eines Anfangsabschnitts der natürlichen Zahlen genau gleich der Summe der dritten Potenzen dieser Zahlen ist.
Small is beautiful
Problemstellung. Tim geht mit seinem Hund am Ufer des Sees spazieren. Er geht vorweg und hin und wieder wirft er einen Ball ins Wasser, den der Hund dann möglichst schnell wieder herbeiholen soll. Tim stellt fest, dass der Punkt, an dem der Hund ins Wasser springt, ziemlich geschickt gewählt ist. Wo liegt der günstigste Punkt für den Sprung ins Wasser? Wir nehmen an, dass der Hund zehnmal schneller laufen kann als schwimmen und dass Tim den Ball 10 m weit vom Ufer wegwirft (Devlin, 2005, S. 19-25).
Lösungsvorschlag. Berechne die Längen der Teilstrecken in Abhängigkeit vom „Absprungpunkt“. Errechne daraus den Zeitbedarf als Funktion dieses Punktes. Finde das Minimum dieser Funktion. Nutze aus, dass die Kurve an der Minimalstelle eine horizontale Tangente besitzt. Bilde die Ableitung der Funktion. Setze die Ableitung gleich null. Löse diese Gleichung nach dem Ort auf. Fertig. Die Kanone hat ihr Werk getan. Der Spatz ist tot. Das Verständnis für das Ergebnis auch. Das ist Sekundarstufe-II-Routine; jedenfalls ist es keine kreative Mathematik.
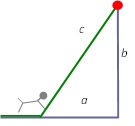
Alternativlösung. Mit jedem Satz, den der Hund entlang des Ufers macht, verringert sich die Länge a der uferseitigen Kathete und auch die Länge der Hypotenuse c. Der Hund sollte spätestens dann ins Wasser springen, wenn die Verringerung von c die Verringerung von a nicht mehr aufwiegt.
Wie verändert sich c, wenn sich a um einen kleinen Hundesatz verringert? Die Hypotenuse wird um den Ballpunkt herum geringfügig geschwenkt. Es entsteht ein kleines Dreieck unterhalb der Uferlinie, das man als näherungsweise rechtwinklig ansehen kann. Die Hypotenuse ist ein kleiner Teil des Wegs des Hundes. Eine Kathede des kleinen Dreiecks entspricht der Länge, um die sich die Wasserstrecke, die Hypotenuse, verringert. Der Hund sollte ins Wasser springen, wenn die Hypotenuse das Zehnfache der Kathede beträgt, wenn also der eingesparte Wasserweg den Hundesatz längs des Ufers gerade aufwiegt.
Die Ähnlichkeit dieses kleinen Dreiecks mit dem großen des Bildes sagt uns, dass der Hund die Strecke bis zum Fußpunkt des Lotes in derselben Zeit durchschwimmen könnte, die er – sozusagen über das Wasser rennend – bis zum Ball brauchte. Jetzt nutzen wir noch den Satz von Pythagoras und finden: Der Hund muss etwa einen Meter vor dem Fußpunkt springen (a ≈ 1005 mm).
Wem das jetzt zu knapp geraten ist, der findet eine ausführlichere Darstellung in meiner Querbeet-Sammlung:
Es ist das Problem mit der Nummer 19.
Anregungen für das schöpferische Denken gibt es hier.
Das Blickwinkel-Problem
Problemstellung. Wir sind in Frankfurt auf der Zeil. Torsten folgt einer Frau, rein zufällig. Ihre Beine faszinieren ihn. Er geht näher ran, um diese unter optimal großem Blickwinkel zu sehen. In welcher Entfernung ist der Blickwinkel auf die Beine am größten? (Drösser, 2007/2010, S. 130-133)
Lösungsvorschlag: Offensichtlich wird der Blickwinkel a bei zunehmender Annäherung an die Dame zunächst immer größer. Aber irgendwann dreht sich der Trend um. Wenn Sie unmittelbar hinter der Dame stehen, ist der Blickwinkel wieder sehr klein. Was nun ist der optimale Abstand, der Punkt also, bei dem sich der Trend umkehrt?
Berechnet wird zunächst die funktionale Abhängigkeit des Blickwinkels vom Abstand. Das leistet der Arcustangens, zweimal angewendet. Die Ableitung dieser Funktion wird gleich null gesetzt. Die daraus folgende Gleichung ist noch nach dem Abstand aufzulösen.
Alternativlösung. Die Aufgabe habe ich meinen Master-Studenten in der Lehrveranstaltung „Problemlösen“ gestellt. Die meisten kamen mit der eben beschriebenen Standardlösung. Aber einer der Studenten hatte eine deutlich abweichende Idee. Er zeichnete einen Kreis, der durch Anfangs- und Endpunkt der Beine der Dame geht und der den Augenhorizont des Herrn berührt. Er behauptete, dass dieser Berührungspunkt der ideale Punkt für die Augen sei. Das komme so aus dem Bauch heraus. Ich ermutigte ihn mit den Worten: Gute Idee, Originalität geht vor Perfektion, aber der Beweis müsse schon sein. Er hat diesen inzwischen wohl auch gefunden. Ich finde seine Lösung hinreißend. Ich schreibe sie hier in meinen Worten auf.
Wir zeichnen mehrere Kreise durch die Beinendpunkte. Je größer die Kreise werden, umso kleiner wird der Umfangswinkel, unter dem man die Beine sieht. Der Satz vom Umfangswinkel besagt ja, dass diese Kreise die geometrischen Orte für gleiche Betrachtungswinkel sind. Jetzt ist klar: Solange der Umfangswinkel groß ist und der Kreis entsprechend so klein, dass der Kreis den Blickhorizont des Mannes nicht berührt oder schneidet, besteht für den Mann keine Chance, die Beine unter diesem Winkel zu sehen (es sei denn, er geht in die Hocke und macht sich noch mehr lächerlich). Erst wenn der Winkel so klein und damit der Kreis so groß ist, dass er den Blickhorizont des Mannes berührt, kann der Mann die Beine unter genau diesem Winkel sehen. Er muss nur bis zu diesem Berührpunkt an die Dame herangehen.
Der Rest ist einfache Kalkulation. Der Satz des Pythagoras liefert für den Abstand die Quadratwurzel aus dem Produkt von Augenhöhe multipliziert mit der um die Beinlänge verminderten Augenhöhe. Torsten hat seine Augen auf der Höhe von 170 cm und die Beinlänge der Frau beträgt 70 cm. Dann muss Torsten immerhin bis auf 130 cm an die Dame herangehen, wenn er einen optimalen Blick haben will. Noch näher dran würde Torsten wohl eine Ohrfeige riskieren.
Quellen
Devlin, Keith: Der Mathe-Instinkt. Klett-Cotta 2005
Drösser, Christoph: Der Mathematik-Verführer. Rowohlt 2007/2010
Grams, Timm: Klüger irren – Denkfallen vermeiden mit System. Springer 2020

Das ist ein nettes zeitliches Zusammentreffen. Im nächsten „Spektrum“ (Juli-Ausgabe, erscheint Mitte Juni) erscheint mein Artikel „Kann der Hund Analysis?“. Natürlich geht es darum, wie der Hund den optimalen Absprungpunkt ins Wasser ermittelt. Ergebnis, wie erwartet: Der Hund muss keine Analysis können. Aus seinen persönlichen Eigenschaften (im Wesentlichen dem Verhältnis von Lauf- zu Schwimmgeschwindigkeit) errechnet sich ein optimaler Winkel, und das ganz ohne Nachdenken über einen infinitesimalen Hundeschritt (was ja Analysis in Verkleidung ist). Den Winkel kann der Hund durch Versuch und Irrtum lernen.
Ja, ich stimme zu: Man soll den Hammer zweckmäßig nur verwenden, wenn man sein Ziel nicht besser ohne Nägel erreichen kann. Und es ist immer wieder nett, Minimierungsaufgaben mit originellen nicht-analytischen Mitteln zu lösen. Ja, auch das Induktionsprinzip ist ein Hammer, und zwar einer, an den man sich relativ mühsam gewöhnen muss.
Und trotzdem muss ich um Verständnis für die armen Lehrer werben. Der Hammer allein ist schon schwierig genug. Richtig geeignet ist er für die schwierigen Probleme. Das sind dann zwei Schwierigkeiten auf einmal. Da kann es sogar sinnvoll sein, mit dem Hammer erstmal zwei Bretter zu vernageln, die auch so zusammengehalten hätten.
Als wir die Sache mit den Minimierungsproblemen in der Schule hatten, waren die einzigen Funktionen, mit denen wir ernsthaft umgehen konnten, Polynome. Da war schon das Hundeproblem außer Reichweite. Die Textaufgaben waren denn auch sehr künstlich. Und dann war Abitur. Ja, unbefriedigend. Aber deswegen gar nicht über den Hammer reden?