Fuldaer Brückenkurs Mathematik
 Eingangstest
Zahlenrechnung Aufgabe 1. Dividieren Sie die Zahl 7,18 durch die Zahl 8,17 und geben Sie das Ergebnis auf zwei Nachkommastellen genau an. Dabei soll der Rundungsfehler möglichst gering sein. Die Aufgabe bitte nur mit Papier und Stift bearbeiten. Tragen Sie das Ergebnis in das Feld ein:

Arithmetik Aufgabe 2. Es gibt ein Theaterstück mit dem Titel 2 · 2 = 5. Diese Gleichung wird jetzt bewiesen. Wir beginnen mit etwas Richtigem:

20 = 20

Daraus folgern wir:
- 20 = - 20
16 - 16 - 20 = 25 - 25 -20
16 - 36 = 25 - 45
16 - 36 + 81/4 = 25 - 45 + 81/4
( 4 - 9/2 )2 = ( 5 - 9/2 )2
4 - 9/2 = 5 - 9/2
4 = 5
2 · 2 = 5
Wo steckt der erste Fehler? Markieren Sie die Zeile, die durch eine fehlerhafte Rechenoperation entstanden ist und bestätigen Sie.
Algebra Aufgabe 3. Die Gleichung 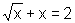 ist nach x aufzulösen. Das geschieht folgendermaßen:
x = 4 - 4x + x2
x2 - 5x + 4 = 0
Wir machen die Probe und setzen das erste Ergebnis in die ursprüngliche Gleichung ein:
2 + 4 = 2
6 = 2
Markieren Sie diejenige der obigen zehn Zeilen, die zu einem Fehlschluss führt. Überlegen Sie, was hinter dem Fehler steckt. Markieren Sie die passende der unten stehenden drei Möglichkeiten.
Rechenfehler
Unerlaubter Umkehrschluss
Falsche Aufgabenstellung
Bestätigen Sie Ihre beiden Auswahlentscheidungen.
Aufgabe 4. Gegeben sind die zwei Funktionen

f(x) = (3x2 - 15x + 18)/(2x - 4)
g(x) = (3x2 - 15x + 18)/(x2 + 3x - 10)

Gesucht sind die x-Koordinaten der Schnittpunkte der zugehörigen Kurven, also diejenigen Werte x, für die f(x) = g(x) gilt. Welcher der folgenden Lösungsvorschläge ist richtig:
Es gibt keine Lösung
Es gibt eine Lösung, nämlich x = 2
Es gibt eine Lösung, nämlich x = -3
Es gibt zwei Lösungen, nämlich x = 2 und x = -3
Wählen Sie eine der vier Möglichkeiten aus und bestätigen Sie.
Wahrscheinlichkeitslehre Aufgabe 5. Große Fernsehshow. Der Supergewinn verbirgt sich hinter einer von drei Türen. Der Kandidat trifft seine Wahl. Die Tür wird jedoch zunächst nicht geöffnet. Der Showmaster öffnet eine der beiden anderen Türen, wohl wissend, dass dahinter eine Ziege als lebende Niete angepflockt ist. Der Showmaster stellt dem Kanditaten nun frei, bei seiner ursprünglichen Wahl zu bleiben, oder die dritte der Türen zu öffnen. Soll er, oder soll er nicht? Welche Antwort ist richtig:
Die dritte Tür öffnen ist günstiger.
Bei der Wahl bleiben ist günstiger.
Es ist egal, welche Tür man wählt.
Wählen Sie eine der drei Möglichkeiten aus und bestätigen Sie.

Aufgabe 6. Ich werfe drei Münzen gleichzeitig und frage, wie groß die Wahrscheinlichkeit ist, dass alle drei die gleiche Seite zeigen, sei es Kopf oder sei es Wappen.
Die Wahrscheinlichkeit dafür, dass alle drei Münzen Kopf zeigen, ist (1/2)3, also gleich 1/8.
Die Wahrscheinlichkeit dafür, dass alle drei Münzen Wappen zeigen, ist ebenfalls 1/8.
Die Wahrscheinlichkeit dafür, dass alle drei die gleiche Seite zeigen, ist also gleich 1/4.
Wie auch der Wurf erfolgt, immer sind notwendigerweise unter den drei Bildern zwei gleiche, seien es nun Köpfe oder Wappen. Die Wahrscheinlichkeit für wenigtens zwei gleiche Münzseiten ist also gleich 100%.
Die Wahrscheinlichkeit dafür, dass auch noch die dritte Münze das gleiche Bild zeigt, ist 1/2. Die Wahrscheinlichkeit, dass alle drei Münzen die gleiche Seite zeigen, ist demnach gleich 1/2.
Da muss eine Aussage falsch sein, da ja die Wahrscheinlichkeit dafür, dass alle drei Münzen die gleichen Seiten zeigen nicht sowohl gleich 1/4 (3.Aussage) als auch gleich 1/2 sein kann (5.Aussage). Markieren Sie die Aussage, in der ein Fehlschluss steckt und bestätigen Sie Ihre Auswahl.
Textaufgaben Aufgabe 7. Eine Flasche kostet mit Korken 100 Cent. Die Flasche kostet 90 Cent mehr als der Korken.
Wieviel kostet der Korken? Cent

Aufgabe 8. Es ist ein Viertel nach drei, also 15:15 Uhr. Welchen Winkel bilden der große und der kleine Zeiger der Uhr?
Der Winkel ist gleich null.
Der Winkel beträgt 7,5°.
Der Winkel beträgt 15°.
Wählen Sie eine Möglichkeit aus und bestätigen Sie.

Zurück zur Leitseite "Fuldaer Brückenkurs Mathematik"

Michael Albrecht, 09.01.04; Timm Grams, 22.06.05, 26.05.07