Architektur
In diesem Abschnitt soll die Architektur und Funktionsweise der Z3 kurz vorgestellt werden. Eine ausführlichere Darstellung wird in R. Rojas, Sixty Years of Computation - The Machines of Konrad Zuse gegeben.
Die Z3 ist eine vollautomatische, d.h. programmgesteuerte Rechenmaschine, die Gleitkommazahlen verarbeitet. Sie besteht aus einem Speicherwerk mit 64 Speicherzellen für Gleitkommazahlen, einem Steuerwerk, daß den Ablauf der Operationen über Mikrosequenzer bestimmt, einem Rechenwerk mit Registern für die Verarbeitung von Gleitkommazahlen sowie Ein- und Ausgabeeinheiten. Programme, auf einem Lochstreifen gespeichert, werden von einem Lesegerät abgetastet und vom Steuerwerk ausgeführt.
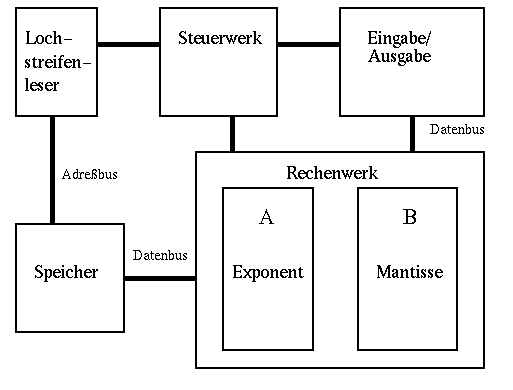
Das Rechenwerk (s. Abb. unten) verarbeitet die Gleitkommazahlen in zwei getrennten Teilen, Teil A verarbeitet die Exponenten, Teil B die Mantissen. Register, zur Aufnahme einer Gleitkommazahl sind durch die Teilung des Rechenwerks ebenfalls in Mantissen- und Exponententeil getrennt. Die Register sind innerhalb eines Teils durch einen Datenbus miteinander verbunden. Es gibt insgesamt vier Registerpaare. Die Registerpaare <Af,Bf> und <Ab,Bb> sind Operandenregister, die Paare <Aa,Ba> und <Ae,Be> sind Hilfsregister (deren Inhalte werden nach jedem Zyklus gelöscht). Durch Öffnen von speziellen Schaltern (Gates) wird die Verbindung eines Registers zum Datenbus geöffnet. Dadurch können Werte zwischen den Registern transportiert werden. Zum Beispiel bewirkt das Öffnen von Ef eine Übertragung des auf Ae stehenden Wertes auf Register Af. Zwischen manchen Verbindungen liegen Schaltungen, die den zu übertragenden Wert um einen einstellbaren Betrag verschieben (Shifter). In jedem Teil befindet sich ein Additionswerk, das durch Schalter (As, Bs) auf Subtraktion eingestellt werden kann. Im Teil B gibt es einen Multiplexer, der je nach Einstellung den Ausgang des Addierers oder das Register Ba mit Be verbindet.
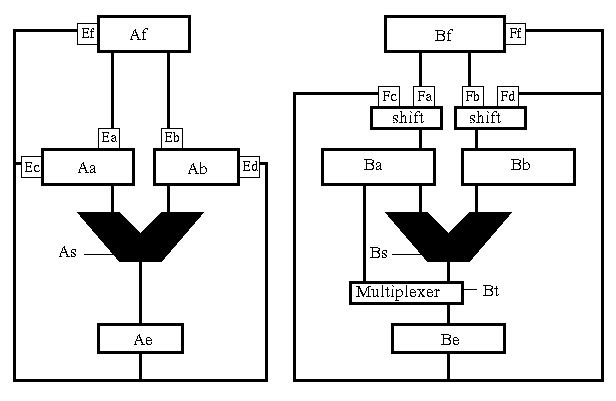
Takt
Die Z3 ist eine getaktete Maschine. Ein Taktzyklus kann grob in zwei Phasen unterteilt werden. In einer Vorbereitungsphase werden Einstellungen für die anschließende Arbeitsphase getroffen. Hier wird beispielsweise der nächste Befehl im Programm decodiert, die benötigten Argumente auf die Register übertragen und die Additionswerke auf Addition oder Subtraktion eingestellt. In der Arbeitsphase wird eine Addition (Subtraktion) in den Additionswerken ausgeführt: die Registerinhalte von Aa und Ab (Ba und Bb im Teil B) werden addiert (subtrahiert), das Ergebnis auf den Ausgang der Addierer gelegt.
Die Einstellungen im Rechenwerk werden vom Steuerwerk vorgenommen. Das Steuerwerk besitzt für jede Rechenoperation eine spezielle Schaltung. Diese Schaltungen nehmen zyklisch die benötigten Einstellungen am Rechenwerk vor und erzeugen dort einen "Zahlenkreislauf". Diese Schaltungen haben Ähnlichkeit mit heute üblichen Mikroprogrammen, sind aber "fest verdrahtet" und werden deshalb als Mikrosequenzer bezeichnet
Befehle und Programmschema
Die Z3 besitzt drei Gruppen von Befehlen: Arithmetik-Befehle (Addition, Multiplikation), I/O-Befehle (Einlesen, Ausgeben) und Speicherbefehle (Laden, Speichern). Der vollständige Befehlssatz und die Anzahl der benötigten Zyklen pro Befehl ist nachfolgender Tabelle zu entnehmen.
| Operation | Anzahl Zyklen |
| Addition | 3 |
| Subtraktion | 4-5 |
| Multiplikation | 16 |
| Division | 18 |
| Quadratwurzel | 20 |
| Einlesen | 9-41 |
| Ausgeben | 9-41 |
| Laden | 1 |
| Speichern | 0 |
Die arithmetischen Befehle beziehen sich auf die Operandenregister <Af,Bf>,im folgendem mit R1 bezeichnet, und <Ab,Bb> im folgendem mit R2 bezeichnet. Die Operation Quadratwurzel bezieht sich nur auf Register R1. Es ist nicht möglich, Argumente einer Rechenoperation explizit, beispielsweise durch Konstanten oder Speicheradressen, anzugeben. Das Ergebnis einer Operation wird normalerweise in R1 abgelegt. Register R2 wird zerstört, d.h. dessen Inhalt ist nach einer Operation undefiniert. Die implizite Semantik einer arithmetischen Operation o ist demnach R1 := R1 o R2 (Ausnahme: Quadratwurzel R1 := Sqrt(R1) ).
Der Befehl Einlesen liest eine auf der Eingabekonsole im Dezimalsystem eingestellte Gleitkommazahl ein, rechnet den Wert in das interne Zahlenformat um und überträgt den Wert auf ein Operandenregister. Welches Operandenregister gewählt wird, hängt von der aktuellen Belegung ab: sind beide Operandenregister frei, so wird die eingelesene Zahl auf das Register R1 eingestellt, andernfalls auf R2.
Ausgeben rechnet den Wert des Registerinhalts R1 in die Dezimaldarstellung um, und zeigt diese an der Ausgabekonsole an. Beide Operandenregister werden dadurch zerstört und freigegeben. Die Anzahl der Zyklen bei den Ein- und Ausgabebefehlen ist abhängig vom Betrag des Exponenten der betreffenden Zahl. Je größer der absolute Betrag des Exponenten ist, desto mehr Zyklen werden für notwendige Unterprogramme (Multiplikation mit 10 bzw. Division durch 10) benötigt.
Der Befehl Laden benötigt als Argument die Adresse der Speicherzelle, deren Inhalt in das Rechenwerk übertragen werden soll. Die Wahl des Zielregisters entspricht dem Vorgehen beim Einlesen.
Der Befehl Speichern benötigt ebenfalls als Argument die Adresse einer Speicherzelle. Das Speichern folgt sinnvollerweise einer arithmetischen Operation oder einer Eingabeoperation. Dabei wird die normalerweise stattfindende Rückübertragung des Ergebnisses auf Register R1 unterbrochen, d.h. der letzte Zyklus einer Rechenoperation wird mit dem Speicherzyklus überlappt. Daraus folgt die Rechenzeit von 0 Zyklen für diese Operation. Beide Register sind nach dieser Operation gelöscht und werden freigegeben.
Bis auf die Befehle Speichern und Laden können die Operationen auch manuell gestartet werden. Dafür besitzt die Maschine an der Konsole die entsprechenden Tasten.
Das Zahlenformat
Die Z3 verwendet intern ein binäres Gleitkommaformat. Eine Zahl
x wird durch die Angabe des Vorzeichens, des Exponenten
a und der Mantisse b spezifiziert.
Der Wert von x ergibt sich aus
x = +/- 2a * b.
Die Angaben a und b werden
im dualen Stellenwertsystem codiert, wobei a ganzzahlig
und vorzeichenbehaftet ist, d.h. a ist eine Zahl im
Zweierkomplement. Die Mantisse ist normalisiert, d.h. b
kann nur Werte 1 <= b < 2 annehmen.
In den Registern und Speicherzellen variiert die Anzahl der Bits für die Kodierung von a und b. Im Speicher werden 7 Bits für a und 14 Bits für b verwendet. Ein Bit wird für das Vorzeichen benötigt. Aufgrund der normalisierten Darstellung braucht im Speicher das höchstwertige Bit nicht mit abgespeichert werden, da dieses immer 1 ist. Im Rechenwerk erhöht sich die Anzahl der Bits. Die Register Aa, Ab und Ae benötigen ein zusätzliches Bit um die Addition der Exponenten zu bearbeiten. Im Teil B wird das höchstwertigste Bit mitgeführt, zwei Extrabits erhöhen die Rechengenauigkeit. Die Register Ba, Bb und Be benötigen noch zusätzlich zwei Bits, um Zwischenergebnisse aufnehmen zu können. Beim Quadratwurzelziehen kann es im Register Ba zu Überläufen kommen, so daß sich dessen Breite noch einmal um ein Bit erhöht. Tabelle gibt einen Überblick über die Bitlänge der Register.
| Register | Länge | Register | Länge | Stellenbreich |
|
Af |
7 |
Bf |
17 |
20...2-16 |
|
Aa |
8 |
Ba |
19 |
22...2-16 |
|
Ab |
8 |
Bb |
18 |
21...2-16 |
|
Ae |
8 |
Be |
18 |
21...2-16 |
Durch die normalisierte Form ist die Zahl Null nicht darstellbar. Deshalb wird jede Zahl mit dem kleinstmöglichen Exponenten (-64) als Null interpretiert. Zahlen mit dem Exponenten 63 stellen den uneigentlichen Grenzwert Unendlich dar. Operationen mit diesen Werten können zu undefinierten Resultaten führen (z.B. 0 dividiert durch 0). Die Z3 erkennt solche Situationen und gibt entsprechende Meldungen aus.