Umweltsimulation mit Tabellenkalkulation
Die Studie ist für fortgeschrittene Teilnehmer des Kurses Umweltsimulation mit Tabellenkalkulation gedacht. Sie zeigt, dass das mikroökonomische Modell der Konkurrenz auf vollkommenen Märkten auf das populationsdynamische Konkurrenz-Modell abgebildet werden kann. Der folgende Text ist ein Leitfaden zur Erstellung des mathematischen Modells. Das Computermodell wird mittels Tabellenkalkulation realisiert. (Ein Arbeitsblatt, das Ergebnis der Studie ist, kann übers Netz geladen werden.)
Unsere Wirtschaft und der Markt funktionieren im Großen und Ganzen nach denselben Gesetzen wie die Biologie. (Tatsächlich wurden die Evolutionsgesetze, noch bevor Charles Darwin es für die Biologie tat, vom Soziologen Herbert Spencer formuliert. Von diesem ist auch das - fälschlich Darwin zugeschriebene - Zitat "survival of the fittest".) Zwischen Unternehmen gelten ähnliche Konkurrenzbeziehungen wie zwischen Populationen.
Wir beschränken uns zunächst auf die Betrachtung einer Wirtschaftsperiode: Die Haushalte treffen in Abhängigkeit vom Angebot, den Preisen sowie dem verfügbaren Budget ihre Kaufentscheidungen. Wir beschränken uns ferner auf die Betrachtung eines einzigen Produkts. Es gibt zwei Anbieter, die mit diesem Produkt am Markt miteinander konkurrieren.
Wir gehen davon aus, dass die Nachfrage x nach dem Produkt mit dem Preis p linear fällt: x = B(1-p/A). Die Konstante A ist der Höchstpreis: zu höheren Preisen lässt sich das Produkt nicht mehr verkaufen. Die Sättigungsmenge wird mit B bezeichnet: mehr lässt sich am Markt nicht unterbringen, selbst wenn man die Ware verschenkt. Auflösen nach p ergibt die Nachfragefunktion
p = p(x) = A(1-x/B)
Darin ist p der erzielbare Preis bei einer angebotenen Menge x. Wir betrachten nun zwei Anbieter. Der Anbieter j (j=1 oder j=2) bietet die Menge xj des Produkts an. Er hat die Fixkosten kj und den Proportionalitätsfaktor qj für die variablen Kosten. Das ergibt die Kostenfunktion
Cj(xj) = kj + qj× xj
für den Anbieter j. (Hierbei wird ein lineares Ertragsgesetz vorausgesetzt. Also: Der Ertrag - die angebotene Menge - wächst linear mit dem für die variablen Kosten verantwortlichen Faktoreinsatz.) Die Stückkosten für den Anbieter j sind gleich
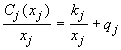
Wir bezeichnen qj als konstanten Stückkostenanteil. Das gesamte Angebot x ist die Summe der angebotenen Teilmengen:
![]()
Der Anbieter j kann je Exemplar seines Produkts einen Gewinn erzielen, der sich aus der Differenz aus Preis und Stückkosten ergibt.
Die Gewinnspanne, also der Gewinn je Stück, des Anbieters j sei mit gj bezeichnet. Es gilt:
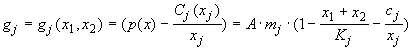
Die Konstanten hierin sind folgendermaßen definiert: Der relative Gewinn mj unter der Bedingung, dass der Höchspreis angesetzt werden kann und nur der konstante Stückkostenanteil berücksichtigt wird, ist gleich
![]() .
.
Die Kapazitätsgrenze Kj für Anbieter j ist gegeben durch Kj = mj B.
Das Verhältnis cj der konstanten Kosten bezogen auf den (um den konstanten Stückkostenanteil reduzierten) Höchstpreis ist gleich
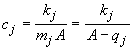 .
.
Multipliziert man die Gewinnspanne mit der Anzahl der produzierten Einheiten, dem Angebot, erhält man den Gewinn. Mit fj bezeichnen wir die so ermittelte Gewinnfunktion des Anbieters j. Die beiden Gewinnfunktionen sind gegeben durch die folgenden Gleichungen:
![]()
![]()
Das dynamische Modell: Herleitung der Zuwachsraten
Wir erweitern nun die Betrachtung auf eine Folge von Perioden und gehen auf ein dynamisches Modell über. Dabei gehen wir davon aus, dass der Anbieter sein Angebot um einen Prozentsatz erhöht, der proportional zum Gewinnzuwachs je zusätzlich produzierter Einheit ist. Zunächst ist also der Gewinn des Anbieters j zu bestimmen.
Der Gewinnzuwachs je zusätzlich produzierter Einheit ergibt sich für jeden der Anbieter, indem man seine Gewinnfunktion (partiell) nach der von ihm angebotenen Menge ableitet. (Vorausgesetzt wird hierbei, dass der Konkurrent seine Produktion jeweils konstant hält.)
![]()
![]()
Je größer dieser Wert für den jeweiligen Produzenten ist, desto größer ist für ihn der Anreiz, sein Angebot zu vergrößern. Wir können die Größen also als proportional zu den Zuwachsraten r1(x1, x2) bzw. r2(x1, x2) der angebotenen Mengen setzen. Für den Proportionalitätsfaktor wählen wir die Bezeichnung R:
![]()
![]()
Das sind bestandsabhängigen Zuwachsraten, wie wir sie in den dynamischen Konkurrenzgleichungen finden:
![]()
![]()
Damit ist der Anschluss an die elementare Theorie der Konkurrenz, die in der Populationsbiologie behandelt wird, hergestellt.
Die Schnittpunkte der der Nullwachstumsgeraden liefern den Gleichgewichtspunkt (x1, x2) = (2K1 /3-K2/3, 2K2/3-K1/3) = B(2m1-m2, 2m2-m1)/3. Damit ist gezeigt: Langfristig überleben beide. Es herrscht Koexistenz. Wir haben es mit einem Oligopol zu tun. Das Simulationsmodell ist im Arbeitsblatt OLIGOPOL der Datei CONTEST.xls realisiert.
Eigen, M.; Winkler, R.: Das Spiel. Naturgesetze steuern den Zufall. Piper, München 1975. Konkurrenz, Selektion und Koexistenz (S. 245 ff.)
Hillebrand, K.: Elementare Mikroökonomik. Fulda 1992. Angebots-, Nachfrage- und Kostenfunktion, Ertragsgesetz, Höchstpreis, Sättigungsmenge, Stückkosten.
Neubäumer, R.; Hewel, B. (Hrsg.): Volkswirtschaftslehre. Grundlagen der Volkswirtschaftstheorie und Wirtschaftspolitik. Gabler, Wiesbaden 1998. Kostenfunktion (S. 75), vollkommener Markt (S. 96), Konsumsumme, Zahlungsbereitschaft, Konsumentenrente (S. 101)
Odum, E. P.: Prinzipien der Ökologie. Spektrum d. Wiss., Heidelberg 1991. Wechselwirkung zwischen Arten (S. 177 ff.), Konkurrenzausschluss (S. 179 ff.)
Wilson, E. O.; Bossert, W. H.: Einführung in die Populationsbiologie. Springer, Berlin, Heidelberg 1973. Exklusionsprinzip und ökologische Nischen (S. 142 f.), Konkurrenzgleichungen (S. 147), Nullwachstumskurven (S. 148)
© Timm Grams, 6. Mai 1999