Umweltsimulation mit Tabellenkalkulation
|
Metapopulation – ein Modell für die Evolution altruistischen Verhaltens
Einführung
 Hier
wird die Frage aus der Lektion „Kooperation unter Egoisten: Axelrods Computerturnier“
erneut aufgegriffen: Wie kommt es zur Evolution von Rücksichtnahme, Fürsorglichkeit
und gar aufopferndem Verhalten angesichts der Tatsache, dass alles Leben vom
Egoismus der Gene bestimmt ist? Axelrods Computerturnier modelliert den Selektionsvorgang
auf der Basis des Gefangenendilemmas, also mit Mitteln der Spieltheorie.
Hier
wird die Frage aus der Lektion „Kooperation unter Egoisten: Axelrods Computerturnier“
erneut aufgegriffen: Wie kommt es zur Evolution von Rücksichtnahme, Fürsorglichkeit
und gar aufopferndem Verhalten angesichts der Tatsache, dass alles Leben vom
Egoismus der Gene bestimmt ist? Axelrods Computerturnier modelliert den Selektionsvorgang
auf der Basis des Gefangenendilemmas, also mit Mitteln der Spieltheorie.
In dieser Lektion wird auf Anleihen aus der Spieltheorie verzichtet. Alles spielt sich im Rahmen der Populationsdynamik ab. Wir akzeptieren nun, dass Altruisten innerhalb einer Population einen Selektionsnachteil haben. Die Altruisten einer Population befinden sich tendenziell also auf dem Rückzug (Individualselektion). Andererseits verbessert ein hoher Anteil an Altruisten die Lebensfähigkeit einer Population (Gruppenselektion).
Diese zwei Auswirkungen des Altruismus werden im Modell von Levins nachgebildet (Wilson, 1975, 2000, S. 110).
Das Modell von Levins
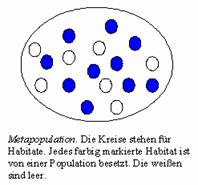
 Unter
einer Metapopulation verstehen wir
eine Population von Populationen. Das Bild oben veranschaulicht die Situation.
Jede Population (Gruppe) besteht aus N Individuen
und sie belegt genau ein Habitat. Unter den Individuen einer Population sind
welche mit dem altruistischen Gen. Populationen mit genau x Altruisten wollen wir x-Populationen nennen. Mit
Unter
einer Metapopulation verstehen wir
eine Population von Populationen. Das Bild oben veranschaulicht die Situation.
Jede Population (Gruppe) besteht aus N Individuen
und sie belegt genau ein Habitat. Unter den Individuen einer Population sind
welche mit dem altruistischen Gen. Populationen mit genau x Altruisten wollen wir x-Populationen nennen. Mit ![]() wird der Anteil der Habitate bezeichnet, die
von den x-Populationen zum Zeitpunkt
t belegt sind. Die Auslöschungsrate für
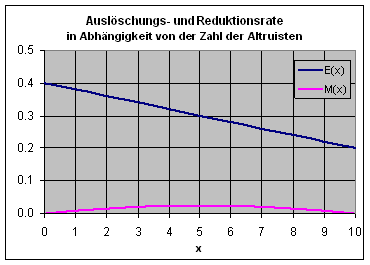
Populationen hängt von der Zahl der Altruisten ab: E(x). Wir gehen hier von
einer linear fallenden Funktion aus: Je mehr Altruisten eine Population hat,
umso weniger ist sie von Auslöschung bedroht. Die nebenstehende Grafik zeigt
eine solche Funktion für die Gruppengröße N
= 10.
wird der Anteil der Habitate bezeichnet, die
von den x-Populationen zum Zeitpunkt
t belegt sind. Die Auslöschungsrate für
Populationen hängt von der Zahl der Altruisten ab: E(x). Wir gehen hier von
einer linear fallenden Funktion aus: Je mehr Altruisten eine Population hat,
umso weniger ist sie von Auslöschung bedroht. Die nebenstehende Grafik zeigt
eine solche Funktion für die Gruppengröße N
= 10.
Gruppenselektion. Nehmen wir vorerst einmal an, dass allein
die Auslöschung von Gruppen wirksam ist. Die Populationsdynamik – also die
zeitliche Änderung der Populationsanteile – wird dann durch die Gleichung ![]() beschrieben.
Demnach verschwinden alle Populationen. Bei den „altruistischen Gesellschaften“
dauert das zwar etwas länger. Aber schließlich sind alle Populationen
unterschiedslos weg. Die Metapopulation wird ausgelöscht, alle Habitate leeren
sich.
beschrieben.
Demnach verschwinden alle Populationen. Bei den „altruistischen Gesellschaften“
dauert das zwar etwas länger. Aber schließlich sind alle Populationen
unterschiedslos weg. Die Metapopulation wird ausgelöscht, alle Habitate leeren
sich.
Neubesiedlung. Wir
wollen nun annehmen, dass ein leer werdendes Habitat grundsätzlich sofort
wieder neu besetzt wird, und zwar von Einwanderern aus der Metapopulation. (Wir
setzen voraus, dass der entsprechende Nachwuchs produziert wird.) Die einzelnen
Populationen enthalten im Durchschnitt ![]() Altruisten. Die
Wahrscheinlichkeit, mit der man bei rein zufälliger Auswahl eines Individuums
der Metapopulation auf einen Altruisten stößt, ist gleich
Altruisten. Die
Wahrscheinlichkeit, mit der man bei rein zufälliger Auswahl eines Individuums
der Metapopulation auf einen Altruisten stößt, ist gleich ![]() . Die Wahrscheinlichkeit, dass eine neue Population bei
rein zufälliger Auswahl der Einwanderer aus dem Pool der Metapopulation genau x Altruisten hat, ist dann gegeben durch
die Binomialverteilung:
. Die Wahrscheinlichkeit, dass eine neue Population bei
rein zufälliger Auswahl der Einwanderer aus dem Pool der Metapopulation genau x Altruisten hat, ist dann gegeben durch
die Binomialverteilung: ![]() .
.
Der Anteil der in einem Zeitschritt frei werdenden Habitate ist
gleich der mittleren Auslöschungsrate ![]() . Da ein
frei werdendes Habitat mit der Wahrscheinlichkeit
. Da ein
frei werdendes Habitat mit der Wahrscheinlichkeit ![]() von einer x-Population belegt wird, erhöht sich
der Anteil der x-Populationen aufgrund
der Neubesiedlung um den Wert
von einer x-Population belegt wird, erhöht sich
der Anteil der x-Populationen aufgrund
der Neubesiedlung um den Wert ![]() . Die Gleichung der Populationsdynamik wird bei
Einbeziehung dieses Effekts zu
. Die Gleichung der Populationsdynamik wird bei
Einbeziehung dieses Effekts zu ![]() .
.
Individualselektion. Neben dem Effekt der Auslöschung und der
Neubesiedlung ist nun nur noch die Reduktion der Zahl der Altruisten in einer
Population zu modellieren. Die Reduktionsrate ![]() ist gleich der
Wahrscheinlichkeit, mit der eine x-Population
zu einer (x-1)-Population wird. Die
Formel für
ist gleich der
Wahrscheinlichkeit, mit der eine x-Population
zu einer (x-1)-Population wird. Die
Formel für ![]() ergibt sich aus der
hypergeometrischen Verteilung (Sachs, 1992): Die Wahrscheinlichkeit für eine
unglückliche Paarung, für das zufällige Aufeinandertreffen eines Altruisten und
eines ungebremsten Egoisten also, ist gegeben durch
ergibt sich aus der
hypergeometrischen Verteilung (Sachs, 1992): Die Wahrscheinlichkeit für eine
unglückliche Paarung, für das zufällige Aufeinandertreffen eines Altruisten und
eines ungebremsten Egoisten also, ist gegeben durch ![]() . Bezugsgröße ist dabei die Anzahl aller möglichen Paarungen.
Diese Wahrscheinlichkeit und die Reduktionsrate setzen wir als zueinander
proportional voraus. Mit dem Selektionskoeffizienten s wird die Reduktionsrate folgendermaßen
festgelegt:
. Bezugsgröße ist dabei die Anzahl aller möglichen Paarungen.
Diese Wahrscheinlichkeit und die Reduktionsrate setzen wir als zueinander
proportional voraus. Mit dem Selektionskoeffizienten s wird die Reduktionsrate folgendermaßen
festgelegt: ![]() . Die obige Grafik zeigt den Verlauf der Kurve für den
Fall N = 10 und s = 0.1.
. Die obige Grafik zeigt den Verlauf der Kurve für den
Fall N = 10 und s = 0.1.
Die Reduktionsrate
ist zur Auslöschungsrate zu addieren, denn sie sorgt genau so wie jene für eine
Verringerung der Zahl der x-Populationen.
Diese wegfallenden x-Populationen
kommen dann den (x-1)-Populationen zu
Gute. Aber auch die x-Populationen
profitieren von diesem Effekt, nämlich durch Reduktion der Altruisten in (x+1)-Populationen. Die Populationsdynamik
wird unter Einbeziehung aller drei Effekte (Gruppenselektion, Neubesiedlung und
Individualselektion) durch die folgende Gleichung beschrieben:
![]()
|
Tabelle der
verwendeten Formelzeichen |
|
|
|
Anzahl der Mitglieder einer Population |
|
|
Anzahl der Altruisten (oder Altruistengene) in einer Population |
|
|
Mittlere Anzahl der Altruisten in den Populationen ( |
|
|
Auslöschungsrate von Populationen mit genau x Altruisten |
|
|
Mittlere Auslöschungsrate |
|
|
Auslöschungsrate von Populationen ohne Altruisten |
|
|
Auslöschungsrate von Populationen aus lauter Altruisten |
|
|
Wahrscheinlichkeit, dass eine neu gegründete Population
genau x Altruisten enthält (Binomialverteilung zur
Wahrscheinlichkeit |
|
|
Wahrscheinlichkeit, zum Zeitpunkt t auf eine Population mit genau x Altruisten zu treffen (relativer Anteil von x-Populationen an der Metaopulation). Die Zeitpunkte sind durchnummeriert: t = 0, 1, 2, 3, … |
|
|
Selektionskoeffizient |
|
|
Reduktionsrate der Altruisten innerhalb einer Population |
Übung
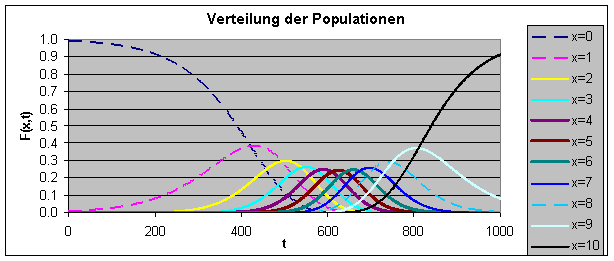
Das Modell von Levins ist im Arbeitsblatt Metapopulation.xls realisiert. Die Populationsgröße ist fest (N = 10). Die folgenden Parameter sind voreingestellt: E(0) = 0.4, E(N) = 0.2 und s = 0.1. Neunundneunzig Prozent der Populationen sind anfangs rein egoistisch und nur ein Prozent der Populationen hat anfangs genau einen Altruisten.
Durch Experimente mit dem Arbeitsblatt soll festgestellt werden, bei welchen Parameterkonstellationen sich der Altruismus durchsetzt.
Faustregel für
siegreichen Altruismus: Die Faustregel dient der groben Orientierung über
die Bedingungen, unter denen sich der Altruismus durchsetzt. Sie basiert auf
der Annahme, dass der Altruismus dann eine Chance hat, wenn die Summe aus
Auslöschungs- und Reduktionsrate mit zunehmendem x fällt. Es wird also verlangt, dass 0 < E(x)-E(x+1) + M(x)-M(x+1).
Daraus folgt die Bedingung ![]() . Der schlimmste Fall tritt für x = 0 ein. Die Bedingung ist jedenfalls erfüllt, wenn s < E(0)-E(N). Das ist bei den voreingestellten Parametern der Fall.
. Der schlimmste Fall tritt für x = 0 ein. Die Bedingung ist jedenfalls erfüllt, wenn s < E(0)-E(N). Das ist bei den voreingestellten Parametern der Fall.
Wie man am voreingestellten Arbeitsblatt sehen kann, setzt sich der Altruismus trotz der ungünstigen Anfangsbedingungen durch. Erhöht man den Selektionskoeffizient s auf beispielsweise den Wert 0.2, kommt der Altruismus nicht mehr zum Zuge. Wählt man gleichmäßigere Anfangsverteilungen, stabilisiert sich der Altruismus auch bei höheren Selektionskoeffizienten.
Literaturhinweise
Sachs, L.: Angewandte Statistik. Springer, Heidelberg 1992
Wilson, E. O.: Sociobiology. The New Synthesis.
Wilson, E. O.: On
Human Nature.
|
|
© Timm Grams, 06.05.2006