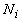die Anzahl der Individuen, die die Strategie i verfolgen. Die Populationsgröße N ergibt sich zu N =
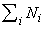. Die Wahrscheinlichkeit 
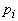, auf ein Individuum der Strategie i zu treffen, ist gleich dem Anteil dieser i-Strategen an der Gesamtpopulation: 
.
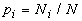Umweltsimulation mit Tabellenkalkulation |
Einführung
Probleme:
In den zwischenmenschlichen Beziehungen und in den Beziehungen zwischen Gruppen stellt sich immer wieder die Frage: Welches Verhalten ist am zweckmäßigsten? Oder anders ausgedrückt: Wie lässt sich mit möglichst wenig Aufwand möglichst viel erreichen?Ziel: Einige Mechanismen der kulturellen Evolution sollen verdeutlicht werden.
Methode: Die Verhaltensmuster werden auf elementare Interaktionen reduziert, so dass sie sich als einfache Zweipersonenspiele modellieren lassen. Diese werden zu Gruppenspielen jeder gegen jeden - jeder sogar gegen sich selbst - erweitert. Bereits so lassen sich wesentliche Interaktionsmechanismen erkunden. Als zweite Untersuchungsmethode wird die ökologische Simulation eingeführt.
Mechanismen der Evolution
Drei Elemente machen jegliche Evolution aus - Dogmatismus, Erfindung und Selektion.
Das mehr oder weniger sture Festhalten am Erprobten und Bewährten, sowie dessen Verbreitung, ist für jeden Fortschritt unerlässlich. Im Chaos gibt es nichts, was sich entwickeln könnte, nichts, wogegen sich ein Kampf lohnen würde. Neue Lösungen, Strukturen, Ideen müssen heranreifen. Aber Dogmatismus allein kann keine Weiterentwicklung bewirken.
Das Schöpferische kommt in die Evolution durch gelegentliche, zufällige kleine Abwandlungen des Überlieferten hinein. Auslöser solcher Abwandlungen sind Übermittlungsfehler, Neukombinationenen und Zusammenfügung alter Lösungen. Jedenfalls entsteht dabei immer etwas unverhersehbar Neues. Der Aufbau höher organisierter Strukturen aus niedrigeren trägt "jedesmal den Charakter des Zufälligen, wenn man so will, den einer Erfindung" (Konrad Lorenz). Das ist die Entzauberung des Schöpfungsaktes: Nicht der geniale Plan ist wichtig, der Zufall spielt die Hauptrolle. Auf diese Weise entsteht naturgemäß viel Ungeeignetes, Fehlerhaftes, zum Absterben Verurteiltes.
Die Ausführung dieses Plans ist Sache der Selektion: Nur was sich im Konkurrenzkampf bewährt, bleibt bestehen. Das ist die Auslese des Bestangepassten. Charles Darwin - und vor ihm Herbert Spencer - sprachen vom "survival of the fittest". Das ist gleichzeitig der Akt der Fehlerbeseitigung. Da nur die zweckmäßigen Strukturen übrigbleiben, entsteht im Nachhinein der Eindruck einer zielgerichteten Entwicklung.
Einen ersten Eindruck davon, wie die Mechanismen der Evolution funktionieren könnten, verschafft das Spiel Zelluläre Automaten und Bibliothek der Formen.
Das Falken-Tauben-Spiel
Wie so ein Selektionsprozess funktionieren könnte, machen wir uns im Falken-Tauben-Spiel klar (Register "Spiele" des Arbeitsblattes FalkeTau.xls). Da wir die Wirksamkeit von Strategien untersuchen wollen, die in einer Population verbreitet sind, müssen wir nun das Spiel in der Variante "Jeder auch gegen sich selbst" spielen (Variante 0). Jeder Spieler vertritt jetzt also nicht ein Individuum, sondern eine bestimmte gemischte Strategie. Spielregeln:
Ökologische Simulation
Die ökologische Analyse ist eine Analyse des Selektionsprozesses (Axelrod, 1987; Eigen, 1971) . Wir betrachten eine Population, deren Individuen nach gewissen (gemischten) Strategien interagieren. Bei diesen Interaktionen bewährt sich eine Strategie besser, die andere schlechter. Das macht den Überlebenserfolg (oder Misserfolg) der Strategen aus. Die Ausbreitung (oder Schrumpfung) einer Strategie innerhalb der Population wird als Wachstumsprozess modelliert.
Sei 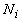die Anzahl der Individuen, die die Strategie i verfolgen. Die Populationsgröße N ergibt sich zu N =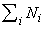. Die Wahrscheinlichkeit 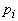, auf ein Individuum der Strategie i zu treffen, ist gleich dem Anteil dieser i-Strategen an der Gesamtpopulation: .
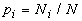Mit aij wird die Auszahlung bezeichnet, die das Individuum der Strategie i beim Zusammentreffen mit einem Individuum der Strategie j erwarten kann (Auszahlungsmatrix).
Das Wachstum der Teilpopulation mit der Strategie i ist proportional zur erwarteten Auszahlung (Gewinnerwartung) je Runde, und die ist gleich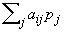 
.
Die Wachstumsrate der Strategie i wird gleich dem Mittelwert des Gewinns der Strategie i über alle möglichen gegnerischen Strategien gesetzt: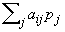 
. Das ist die Produktionsrate der Strategie i. Das Wachstumsgesetz für die Teilpopulation mit der Strategie i ist dann gleich
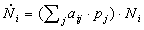
Wer mit der Differentialrechnung nicht vertraut ist, kann die folgende kurze Herleitung übergehen. Er wendet sich besser gleich dem Resultat - dem Wachstumsgesetz der Populationsanteile - und dessen Interpretation zu.
Aus der Definitionsgleichung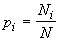 
erhält man mittels Ableitung (Differentiation)
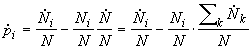
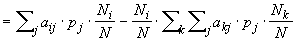
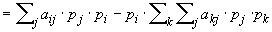
Insgesamt haben wir - wenn wir auf der rechten Seite der Gleichungen noch pi ausklammern - das folgende Wachstumsgesetz für den Anteil der Population mit der Strategie i:
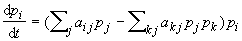
Der zweite Term in Klammern ist die Überschussproduktionsrate. Summiert man die linke und die rechte Seite der Wachstumsgleichungen über alle Populationen i auf, dann steht auf der linken Seite die Änderungsgeschwindigkeit der Summe aller Wahrscheinlichkeiten. Da die Summe der Wahrscheinlichkeiten gleich eins ist, muss diese Änderungsgeschwindigkeit gleich null sein. Die Verminderung der Wachstumsrate einer jeden Strategie um die Überschussproduktionsrate sorgt dafür, dass auch auf der rechten Seite die Summe null herauskommt.
Wird der Wachstumsprozess im Computer simuliert, sprechen wir von ökologischer Simulation.
Das Arbeitsblatt
MemoLessStrategies.xls realisiert die ökologische Simulation des Falken-Tauben-Spiels für Populationen mit zwei gemischten Strategien x1 und x2. Diese Strategien sind frei wählbar. Die Gewinnerwartung eines xi-Strategen, der auf einen xj-Strategen trifft, ist gleich u(xi, xj). Damit ergibt sich die Auszahlungsmatrix zu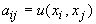
. Die Anteile der Strategien x1 und x2 an der Gesamtpopulation werden mit p1 und p2 bezeichnet.
Gleichgewicht und evolutionär stabile Strategie
Der Einfachheit halber betrachten wir eine Population mit nur zwei Strategien. Der Erwartungswert der Auszahlung für ein Individuum mit der Strategie 1 ergibt sich zu u(x1, x1)
× p1 + u(x1, x2)× p2. Eine elementare Umformung zeigt, dass dies gleich u(x1, p1x1+p2x2) ist. Das heißt: In der Formel für die Gewinnerwartung ist nur x2 durch p1x1+p2x2 zu ersetzen und wir erhalten die erwartete Auszahlung für ein Individuum mit der Strategie 1 innerhalb der durch die Verteilung der Strategien gegebenen Umwelt. In Gleichgewichtspunkt bringen Falken und Tauben gleich viel ein und es lohnt nicht, den Taubenanteil zu verringern oder zu vergrößern. Der Ausgleichsvorgang hin zum Gleichgewicht kommt dadurch zustande, dass bei einer Übervölkerung der Umwelt mit Tauben derjenige begünstigt ist, der den geringeren Taubenanteil hat. Leidet andererseits die Umwelt an einem Taubenmangel - immer gemessen am Gleichgewichtspunkt - dann sind Strategien mit größeren Taubenanteilen begünstigt und wachsen dementsprechend schneller.Unter einer evolutionär stabilen Strategie (ESS) verstehen wir eine Strategie mit folgender Eigenschaft: In einer Population, deren Individuen alle die ESS befolgen, ist eine Abweichung von dieser Strategie für kein Individuum lohnend, eine solche Population ist immun gegen Abweichler. Im Falken-Tauben-Spiel tendiert der Taubenanteil der Gesamtpopulation zum Gleichgewichtswert 5/12 (= 0,42). Die Gleichgewichtsstrategie ist eine evolutionär stabile Strategie.
Anregungen und Übungen
1. Zu untersuchen ist der Selektionsprozess in einer Population, in der zwei gemischte Falke-Tauben-Strategien vertreten sind. Wählen sie die beiden Strategien aus den folgenden aus: Reine Strategien (x=0, x=1), optimale Strategie (x=5/6), evolutionär stabile Strategie (x=5/12). Formulieren sie Vermutungen für das Ergebnis der Evolution für jede der16 Kombinationen. Führen Sie anschließend die ökologische Simulation durch und vergleichen Sie ihre Vermutungen mit den Simulationsergebnissen. Hatten Sie recht? Wenn nicht: was lässt sich daraus lernen? Siehe dazu das Kapitel "Aggression: Die egoistische Maschine und die Stabilität" im Buch von Dawkins (1978).
2.
Erstellen Sie ein Arbeitsblatt für die ökologischen Simulation für Falke-Taube-Populationen mit mehr als zwei gemischten Strategien. Führen Sie ökologische Simulationen für Populationen durch, in denen anfangs drei Strategien vertreten sind.
|
|
© Timm Grams, 29.9.1999