Übungsaufgaben zu

 

Timm Grams

Grundlagen des Qualitäts- und Risikomanagements
Zuverlässigkeit, Sicherheit, Bedienbarkeit

Vieweg Praxiswissen, Braunschweig, Wiesbaden 2001

Vorbemerkung: Die mit einem Sternchen * gekennzeichneten Aufgaben sind grundlegenden Dingen gewidmet. Sie regen zu weiteren Studien an und lassen teilweise verschiedene Ausgestaltungen zu. Sie sind für kleinere Seminararbeiten geeignet.

 

1 Grundbegriffe

1.1 Charakterisieren Sie das 2-aus-2-System bezüglich der Funktions- und der Sicherheitsspezifikation. Was passiert gemäß Spezifikation, wenn ein oder gar beide Subsysteme defekt sind? Welchen Zweck hat die Parallelredundanz in diesem Fall? Wie kann man mit einem solchen System Fail-Safe-Verhalten (siehe Begriffsbestimmung) bewirken?

1.2 Charakterisieren Sie das 2-aus-3-System bezüglich der Funktions- und der Sicherheitsspezifikation. Was passiert gemäß Spezifikation, wenn ein, zwei oder gar alle drei Subsysteme defekt sind.

2 Wahrscheinlichkeitsrechnung und Statistik

2.1 Berechnen Sie die Q-Werte der Tabelle 2.1 des Buches durch numerische Integration der F -Funktion mit Hilfe eines Tabellenkalkulationsprogramms.

2.2 In einer Kiste liegen 1000 Transistoren. Davon sind 10 defekt. Sie entnehmen der Kiste drei Stück. Wie groß ist die Wahrscheinlichkeit dafür, dass alle drei fehlerfrei sind?

2.3 Die Größe der Männer einer bestimmten Bevölkerung sei (175 cm, 5 cm)-normalverteilt. Autos, Betten usw. sind auf eine maximale Größe von - sagen wir einmal - 190 cm ausgelegt. Wie groß ist die Wahrscheinlichkeit, dass jemand zu groß für diesen Standard ist? Schlagen Sie in den Tabellen der Statistik-Lehrbücher nach oder greifen Sie wieder zur numerischen Integration wie in Übung 1.

3 Zuverlässigkeit einfacher Systeme

3.1 Die Nachrichtentafel am alten Times Tower am Times Square hatte ungefähr 13 000 Birnen. Angenommen, die Birnen halten im Mittel 1000 Stunden und ihre Lebensdauer ist exponentialverteilt und die Ausfälle sind unabhängig voneinander, bis wann ist mit einem ersten Ausfall zu rechnen? Ist das Ergebnis plausibel? Sind die Annahmen sinnvoll? (M. L. Shooman: Probabilistic reliability: an engineering approach. Krieger 1990).

3.2 Eine Automatisierungseinrichtung möge etwa 2 000 Elektronikkarten enthalten. Schätzen Sie grob ab, mit welcher Wahrscheinlichkeit die Anlage innerhalb eines Jahres wohl aufgrund des Ausfalls einer Elektronikkarte ausfällt.

3.3 Die Lebensdauer des Taschenrechners bestimmten Typs sei exponentialverteilt mit einem Erwartungswert von 10 Jahren. Von diesem Rechner wurden in einer Ramschaktion 1000 Stück verkauft. Bei Reklamationen innerhalb eines Jahres gibt es das Geld zurück. Mit wie vielen Reklamationen ist innerhalb der Garantiezeit von einem Jahr zu rechnen? Wie groß ist die Wahrscheinlichkeit dafür, dass keine Reklamation auftritt? Wie groß ist die Wahrscheinlichkeit dafür, dass es zu mehr als 100 Reklamationen kommt?

3.4 Für einen Computer mit einer geschätzen konstanten Versagensrate von 6/Jahr wird per Kaufvertrag vereinbart, dass der Verkäufer den Rechner zurücknehmen muss, wenn es im ersten Monat zu mehr als 2 Versagensfällen kommt. Wie groß ist das Risiko (die Wahrscheinlichkeit) für die Rücknahme?

3.5 Das älteste Transatlantik Telefonkabel wurde 1956 in Betrieb genommen und bis 1965 gab es keinen Ausfall. Die Verbindung besteht aus zwei unabhängigen Leitungen - eine je Übertragungsrichtung - von 2 000 Meilen Länge. Die Verstärker haben einen Abstand von 40 Meilen. Jeder besteht aus etwa 60 Teilen. Angenommen wird, dass die Teile unabhängig voneinander ausfallen und dass alle dieselbe Ausfallrate besitzen. Welchen Wert darf die Ausfallrate höchstens haben, wenn nur ein Verstärkerausfall innerhalb von 20 Jahren akzeptiert wird? Präziser: Die Wahrscheinlichkeit dafür, dass es zu mehr als einen Ausfall kommt, soll kleiner als 1% sein.

3.6 Gegeben sei ein System, dessen Ausfallrate mit der Zeit immer größer wird. Mit einer Konstanten c sei sie gegeben durch l(t) = c× t. Bestimmen Sie die MTTF des Systems. Hinweis: Etwas Nachdenken bringt hier mehr als große Herumrechnerei. Alle benötigten Formeln und Zusammenhänge stehen im Buch.

4 Qualitätskontrolle und Zuverlässigkeitsschätzung

4.1 Sie sollen eine Lieferung elektronischer Schaltkreise begutachten. Der Test eines jeden Schaltkreises ist sehr aufwendig, so dass Sie sich auf eine Stichprobengröße von N = 10 beschränken müssen. Sie wollen zu 80 % sicher sein, dass höchstens 30 % der Geräte fehlerhaft sind. Wie viele Geräte der Stichprobe dürfen fehlerhaft sein? Wie sieht die Sache bei einer Stichprobengröße von N = 20 aus?

4.2 Ein zyklisch arbeitendes Programm mit einer Zyklusdauer im Millisekundenbereich soll eine Versagensrate von höchstens 10-4/h besitzen. Das ist eine moderate Anforderung an die Zuverlässigkeit. Diese Versagensrate führt auf längere Sicht zu etwa je einem Versagensfall jährlich. Entwerfen Sie einen Test, mit dem die Versagensrate mit einer Irrtumswahrscheinlichkeit von 5 % nachgewiesen werden kann. Begründen Sie die folgende Aussage: "The quantification of life-critical software reliability is infeasible using statistical methods" (Butler, R. W.; Finelli, G. B.: The Infeasibility of Quantifying the Reliability of Life-Critical Real-Time Software. IEEE Trans. on Software Engineering, 19 (January 1993) 1, 3-12). Anmerkung: Von sicherheitsrelevanter Software wird eine Versagensrate unter 10-7/h gefordert.

4.3 Für ein Programm wurden - bei konstantem Operationsprofil - bisher folgende Versagensabstände (in Sekunden) gemessen: 76, 38, 84, 140, 136, 13, 49, 177, 40, 7. Schätzen Sie die Versagensrate bzw. deren Kehrwert, den mittleren Versagensabstand, ab und geben Sie näherungsweise das Vertrauensintervall zur Sicherheit von 90% an. Wenden Sie die folgenden beiden Methoden an.

  1. Abschätzung unter der - eigentlich unzutreffenden - Annahme, dass der zentrale Grenzwertsatz der Statistik anwendbar ist (Abschnitt 2.4).
  2. Zuverlässigkeitsschätzung nach Abschnitt 4.2.

Vergleichen Sie die Ergebnisse. Sind sie plausibel?

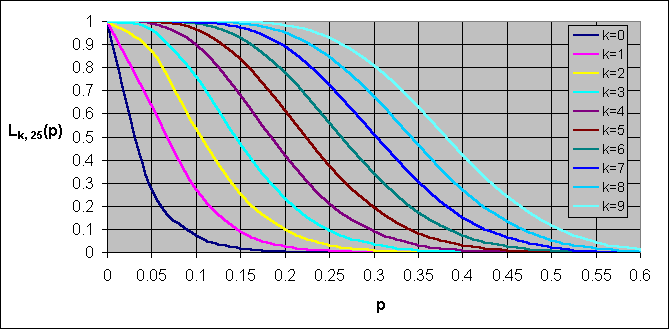
4.4 In der folgenden Grafik finden Sie die Operationscharakteristiken L0,25(p), L1,25(p) ... L9,25(p). Für den Test einer Lieferung von Geräten wird eine Stichprobe von 25 Geräten genommen. Festzustellen ist mit einer Sicherheit von 90 %, dass die Fehlerwahrscheinlichkeit der gelieferten Geräte höchstens gleich 20 % ist.

  • Auf welchen Wert ist die Obergrenze k für die Anzahl fehlerhafter Geräte festzulegen?
  • Welcher Fehlerwahrscheinlichkeit darf der Lieferant in seiner Lieferung höchstens zulassen, wenn er sicher gehen will, dass seine Lieferung bei der gewählten Grenze k mit höchstens 10-prozentiger Wahrscheinlichkeit abgelehnt wird (Lieferantenrisiko).
  • Erläutern Sie ihr Ergebnis anhand der Operationscharakteristik.

5 Diagnostizierbarkeit und Fehlertoleranz

5.1 Ein Computersystem möge aus 8 Rechnern bestehen. Jeder dieser Rechner überwacht jeden anderen. Wie viele Rechnerausfälle lassen sich sicher diagnostizieren? Ist das System 2-diagnostizierbar? 3-diagnostizierbar? 4-diagnostizierbar? Begründen Sie die Antwort.

5.2 Gegeben sei ein 2-Diagnosezyklus von 5 Computern wie in Bild 5.1 (S. 31). Folgende Defektmeldungen mögen vorliegen (alle anderen Meldungen sind Intaktmeldungen): 0 ® 2, 1 ® 2, 1 ® 3, 2 ®  3, 2 ®  4. Was lässt sich aus diesem Diagnoseergebnis über die Computer aussagen? Wieviele Computer sind defekt? Welche? Geben Sie schlüssige Begründungen für Ihre Antworten. Wie verhält sich die Sache bei folgendem Diagnoseergebnis: 0 ®  2, 1 ®  2, 2 ®  3, 3 ®  4, 4 ®  0. Nehmen Sie in beiden Fällen an, das je höchstens zwei Computer defekt sind.

5.3 Gegeben sind sieben Computer A, B, C, D, E, F, G. Jeder Computer wird von allen anderen diagnostiziert (Also: Jeder diagnostiziert jeden anderen!). Wir setzen voraus, dass ein intakter Computer stets auch eine korrekte Diagnose erstellt. Auf die Diagnoseergebnisse defekter Computer ist dagegen kein Verlass. Nur Defekte werden gemeldet. Wir setzen voraus, dass höchstens drei der Computer defekt sind. Zur Zeit liegen folgende Fehlermeldungen vor: A, C, E, F und G melden jeweils B und D als defekt. B meldet C, D und E als defekt. D meldet keinen Defekt. Wieviele Computer sind defekt? Welche? Geben Sie schlüssige Begründungen für Ihre Antworten.

6 Sicherheitstechnik

6.1 Führen Sie den Sicherheitsnachweis für die Antivalenz-Überwachungseinrichtung. Die Fehlerliste - also die Liste der zu berücksichtigenden Fehler - umfasst alle einfachen Fehler der Art "Ausgangsvariable eines Logikbausteins fest-auf-0 (stuck-at-0) oder fest-auf-1 (stuck-at-1)". Geben Sie an, welche Forderungen an die Eingangssignale der Überwachungseinheit gestellt werden müssen, wenn sichergestellt sein soll, dass jeder zu berücksichtigende Fehler in der Überwachungseinheit rechtzeitig erkannt wird.

6.2 Wie lässt sich die Forderung nach Unabhängigkeit der Fehlererkennung vom Prozessverhalten verwirklichen. Hinweis: Setzen Sie vor jeden Eingang der Schaltung ein Exklusiv-Oder-Gatter und verknüpfen Sie damit jedes der Eingangssignale mit einem weiteren Signal. Alle diese zusätzlichen Signale werden von einem Generator erzeugt. Der Generator sorgt für eine Dynamisierung der Eingangssignale der Antivalenz-Überwachungseinrichtung. Beschreiben Sie die Anforderungen an diesen Generator.

6.3 Unter einer 1-aus-3-Schaltung wollen wir eine Schaltung verstehen, die genau dann den Wert eins liefert, wenn von den drei Eingangssignalen genau eines den Wert eins hat. In allen anderen Fällen soll der Wert null herauskommen. Entwerfen Sie eine fehlersichere 1-aus-3-Schaltung auf der Basis des Konzepts aus Bild 6.2.

6.4 Führen Sie den Sicherheitsnachweis für die Schaltung der Übung 6.3 durch. Legen Sie die Wartungsstrategie (das Wartungsintervall) fest. Vorausgesetzt sei eine Fehlerrate je Gatter von 10-8/h. Die Wahrscheinlichkeit für einen weiteren Fehler soll kleiner als 10-4 sein.

7 Fehlerbaumanalyse

7.1 Wichtig für den Operateur eines Kernkraftwerkes ist, zu wissen, ob der Reaktor läuft oder nicht. Das Warnsystem besteht aus drei Meldeeinheiten bestehend aus je einem Sensor und einer Anzeigelampe. Bei fehlerfreiem Betrieb geht die Lampe an, sobald der Reaktor hochgefahren wird; und sie verlöscht, sobald der Reaktor heruntergefahren ist. Für den Operateur bedeuten ein, zwei oder drei Anzeigelichter, dass der Reaktor läuft. Falls keine Lampe leuchtet, hält er den Reaktor für ausgeschaltet. Die Lampen mögen perfekt sein. Die Wahrscheinlichkeit darfür, dass ein Sensor den Ein-Zustand nicht korrekt anzeigt, sei gleich p, und die Wahrscheinlichkeit, dass ein Sensor den Aus-Zustand nicht korrekt anzeigt, sei q. Zu berechnen sind die Wahrscheinlichkeiten POFF, dass der Operateur den Aus-Zustand nicht korrekt ermittelt, und die Wahrscheinlichkeit PON, dass er den Ein-Zustand nicht erkennt. Wie ändern sich diese Zahlen, wenn der Operateur seine Entscheidungsregel dahingehend ändert, dass er den Aus-Zustand immer dann annimmt, wenn höchstens eine Lampe brennt. Bei zwei oder drei brennenden Lampen liegt für ihn dann der Ein-Zustand vor. Zahlenwerte: p =0.1, q = 0.01 (M. L. Shooman: Probabilistic reliability: an engineering approach. Krieger 1990).

7.2 Zu entwickeln ist der Fehlerbaum für das unerwünschte Ereignis "Motor startet nicht" für einen Verbrennungsmotor. Der Verbrennungsmotor möge zwei parallele - Zündungseinrichtungen besitzen. Die Zündung ist also insoweit redundant, als eine dieser Einrichtungen für eine erfolgreiche Zündung ausreicht. Weitere für den Start erforderliche (nicht redundante) Komponenten sind: die Brennstoffzufuhr und der Vergaser.

7.3* Erläutern Sie die wesentlichen Prinzipien der Fehlerbaum-Analyse. Sehen Sie in der relevanten angegebenen Literatur nach folgenden Begriffen: Fault Tree und Cut Set. (Diese Methode wird in der Literatur zur Risikoanalyse ausgiebig behandelt. Die Fehlerbaum-Analyse umfasst Näherungsverfahren, die eine Risikoanalyse sehr komplexer Anlagen erlauben. In der Risikoanalyse kerntechnischer Anlagen gehört die Fehlerbaumanalyse zu den Standardverfahren.)

7.4* Der Abschnitt 6.3 enthält die elementare Analyse eines parallelgeschalteten Verstärkers auf Basis der Ausfalleffektanalyse. Ermitteln Sie die (zeitabhängige) Systemausfallrate gemäß Abschnitt 3.3. Wenden Sie das "Common cause failure"-Modell an (Abschnitt 7.3). Stellen Sie heraus, in welchen Punkten das Modell unrealistisch ist. Wie steht es mit der Unabhängigkeit der Ausfallarten? Überlegen Sie sich, ob es wenigstens im Sinne einer pessimistischen Abschätzung einen Wert hat.
Hinweis: Verwenden Sie die Tatsache, dass im vorliegenden Fall des nicht gewarteten und nicht reparierten Systems die Summe aus (zeitabhängiger) Fehlerwahrscheinlichkeit und Überlebenswahrscheinlichkeit gleich eins ist, und dass diese Relation auch für jedes seiner Subsysteme gilt.
Zusatz: Erstellen Sie zur Behebung der Mängel des CC-Modells ein Markoff-Modell des Systems. Vergleichen Sie die Ergebnisse des CC-Modells mit denen des Markoff-Modells (mittels Tabellenkalkulationsprogramm). Welches der Modelle liefert die pessimistischeren Aussagen? Geben Sie Begründungen an.

7.5 Ein Auto fährt mit normaler Geschwindigkeit auf eine Kreuzung zu. Ein Stop-Schild zeigt an, dass eine Hauptstraße kommt. Wie groß ist die Wahrscheinlichkeit, dass es auf der Kreuzung zu einem Zusammenstoß kommen wird? Verwenden Sie die Fehlerbaumanalyse. Schätzen Sie die Wahrscheinlichkeiten für die Basisereignisse möglichst realitätsnah ab. Zur Orientierung: häufig (10-1), gut möglich (10-2), eher selten (10-3), sehr selten (10-4), unwahrscheinlich (10-5).

8 Ereignisbaumanalyse

8.1 Leiten Sie nach der Methode des Ereignisbaums die Fehlerwahrscheinlichkeit eines 2-aus-3-Systems her - bezogen auf die funktionale Spezifikation. Die drei Subsysteme mögen die gleiche Fehlerwahrscheinlichkeit p haben. Ergebnis: p2-aus-3 = 3p2 - 2p3.

8.2 Leiten Sie die Formel für die Fehlerwahrscheinlichkeit des 2-aus-3-Systems unabhängig von der vorigen Aufgabe nach folgender Methode her:

  1. Schreiben Sie die Indikatorfunktion als Boolesche Funktion.
  2. Ersetzen Sie die Booleschen Operatoren durch arithmetische.
  3. Fassen Sie die Indikatorvariablen und die Funktion als Zufallsvariablen auf.
  4. Bilden Sie den Erwartungswert der Funktion.

Benutzen Sie, dass der Erwartungswert einer Indikatorvariablen gleich der Fehlerwahrscheinlichkeit des entsprechenden Subsystems ist. Dasselbe gilt für die Indikatorfunktion, die ja Indikatorvariable des Gesamtsystems ist.

8.3 Geben Sie im Programm FaultTree+ den Fehlerbaum für das Beispiel des Zweiturbinen-Kraftwerks ein und berechnen Sie die Wahrscheinlickeit des Top-Ereignisses boiler overheat.

8.4 Geben Sie im Programm FaultTree+ den Ereignisbaum für das Beispiel des Zweiturbinen-Kraftwerks ein und verifizieren Sie das obige Ergebnis (es erscheint auch im Haupttext).

8.5* Ein Kommunikationssystem möge aus einem Sender und einem Empfänger bestehen, die auf eine bestimmte Frequenz abgestimmt sind. Zur Erhöhung der Zuverlässigkeit gibt es ein zweites (redundantes) Gerätepaar, das auf einer anderen Frequenz arbeitet, ansonsten aber gleich ist. Außerdem gibt es für jeden Empfänger eine Umschalteinheit, so dass er auf der einen oder der anderen Frequenz empfangen kann. Die Lebensdauern der Geräte sind exponentialverteilt. Die Werte der Ausfallraten:

  • Sender: l
  • Empfänger: l
  • Umschalteinheit: l /10

Zeichnen Sie den Fehlerbaum und den Ereignisbaum des Systems. Geben Sie die Indikatorfunktion des Systems an. Ermitteln und zeichnen Sie die Zuverlässigkeitsfunktion des Systems (M. L. Shooman: Probabilistic reliability: an engineering approach. Krieger 1990). Verwenden Sie den Hinweis aus Aufgabe 7.4.

9 Zuverlässigkeit komplexer Systeme

i

ni

1

15 206

2

551

3

343

4

242

5

73

6

32

7

12

8

2

9.1 In einem bekannten Experiment zur Diversitären Programmierung wurden - ausgehend von einer gemeinsamen Spezifikation - 27 Programmversionen unabhängig voneinander erstelllt. Dies Programme wurden schließlich mit einer Million Testdatensätze überprüft (Knight, J. C.; Leveson, N. G.: Correlated failures in multiversion software. SAFECOMP '85. Proceedings of the 4th IFAC Workshop, Como, Italy, 1985, Pergamon Press, 159-165). Dabei ergab sich die nebenstehende Statistik, in der jeweils die Anzahl ni derjenigen Testfälle aufgeführt ist, bei denen genau i Versionen versagen. Ermitteln Sie die mittlere Versagenswahrscheinlichkeit p und die Versagenswahrscheinlichkeit pdiv für ein diversitäres Zweiversionen-System.

9.2 Beantworten Sie die folgenden Fragen und begründen Sie kurz Ihre Antworten.

  • Eine Software (ein konstantes System) hat bei konstantem Operationsprofil nicht notwendigerweise eine konstante Systemversagensrate. Warum?
  • Das Parallelausführen von Programmen, die von unabhängigen Programmierteams aber nach derselben Spezifikation erstellt worden sind und die sich wechselseitig überwachen, nennt man diversitäre Programmierung. Warum kann man die Versagenswahrscheinlichkeiten der parallelredundanten Systeme nicht nach derselben Formel berechnen, die für die Unverfügbarkeit von redundanten Hardware-Systemen gilt?

10 Wartung und Reparatur: Verfügbarkeit

10.1 Berechnen Sie den Zeitverlauf der Unverfügbarkeit des 2-aus-3-Systems mit Umschalteinrichtung. Die Ausfallrate jeder der Komponenten sei lk = 0.1/a. Die Ausfallrate der Umschalteinheit sei lU = 0.01/a und die Reparaturrate für jede Komponente und die Umschalteinheit sei m = 100/a. Verwenden Sie für die Analyse ein geeignetes Werkzeug, z. B. das Programm FaultTree+.

10.2* Berechnen Sie die mittlere Unverfügbarkeit des allgemeinen einfehlertoleranten und gewarteten Systems aus n Komponenten und vergleichen Sie diese mit der mittleren Unverfügbarkeit die sich - bei gleicher Komponentenzahl - ergäbe, wenn das System nicht fehlertolerant wäre. Führen Sie geeignete Näherungen ein unter der Annahme, dass das Wartungsintervall T wesentlich kleiner als die MTTF der Komponenten ist (Annahmen wie Abschnitt 10.2, S. 71).

10.3* Ein System mit der Ausfallrate l wird periodisch mit dem Wartungsintervall T gewartet. Wird bei der Wartung ein Fehler erkannt, dann wird repariert. Die Reparaturrate ist m . Zeigen Sie, dass unter den Bedingungen l T<<1 und l /m <<1 für die Unverfügbarkeit des Systems die Abschätzung U»½ l T+l/m gilt (Dormant Failure with Periodic Inspection Model).

10.4* Sei MTBF der mittlere Ausfallabstand eines nichtredundanten Systems aus n Komponenten mit jeweils gleicher Ausfallrate. Der mittlere Ausfallabstand des einfehlertoleranten System mit derselben Zahl von Komponenten wird mit MTBFS bezeichnet. (Das tiefgestellte S steht für "sicher" oder "einfehlersicher".) Mit MTTR wurde im Abschnitt 10.3 der Kehrwert der Reparaturrate bezeichnet. Unter der Voraussetzung MTTR << MTBF ergab sich dort, dass sich durch die Fehlertoleranz eine Vergrößerung des mittleren Ausfallabstands um etwa den Faktor MTBF/MTTR ergibt, genauer:

.

Weisen Sie nach, dass diese Beziehung auch für das periodisch gewartete System gilt, wenn man für MTTR das halbe Wartungsintervall (T/2) einsetzt.

10.5 Ein elektronisches System möge aus Komponenten bestehen, für die eine konstante Ausfallrate angesetzt werden kann. Das System arbeitet mit Fehlererkennung. Allerdings ist nur ein Teil der Komponentenausfälle im Betrieb erkennbar. Wir bezeichnen mit l' die Summe der Ausfallraten derjenigen Komponenten, deren Ausfälle nicht erkennbar sind, und l'' ist die Summe der Ausfallraten von Komponenten mit Fehlererkennung. Erkannte Fehler werden mit der Reparaturrate m beseitigt. Das System gilt erst als ausgefallen, wenn ein nichterkennbarer Fehler vorliegt. Berechnen Sie die MTTF des Systems. Ermitteln Sie das Ergebnis durch stationäre Analyse des untenstehenden Markoff-Modells unter Verwendung der Formel für die Unverfügbarkeit. Geben Sie alle Schritte der Herleitung an und beschreiben Sie kurz, was Sie machen. Geben Sie die Näherung für relativ rasche Reparatur an (m >> l' + l''). Interpretieren Sie das Ergebnis.

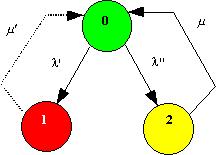
10.6 Berechnen Sie die MTTF eines zweifehlertoleranten Systems aus n gleich zuverlässigen Komponenten (Ausfallrate = l ) unter der Voraussetzung, dass einzelne Komponentenfehler nicht repariert werden. Ermitteln Sie das Ergebnis durch stationäre Analyse des untenstehenden Markoff-Modells unter Verwendung der Formel für die Unverfügbarkeit. Geben Sie alle Schritte der Herleitung an und beschreiben Sie kurz, was Sie machen.

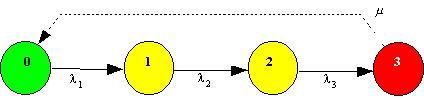
10.7 Leiten Sie die Formel für die Unverfügbarkeit eines 3-aus-4-Systems her. Die Unverfügbarkeit einer jeden der Komponenten sei gleich U. Die Unverfügbarkeiten der verschiedenen Komponenten sind voneinander statistisch unabhängig. Stellen Sie die Indikatorfunktion auf und führen Sie dann die Analyse mittels Ereignisbaumanalyse durch.

10.8 Wir betrachten ein System mit zwei Ausfallarten. Nur eine davon ist gefährlich im Sinne der Sicherheitsspezifikation. Die Ausfallrate für den gefährlichen Zustand ist gleich l' und die für den ungefährlichen ist gleich l'' (siehe nebenstehendes Markoff-Modell). Das System wird in regelmäßigen Zeitabständen gewartet. Das Wartungsintervall hat die Länge T. Ermitteln Sie die sicherheitsbezogene mittlere Unverfügbarkeit des Systems.

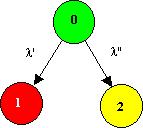
10.9* Gesucht ist die System-Ausfallrate des einfehlertoleranten Systems unter der Voraussetzung, dass es aus n Komponenten besteht, die allesamt dieselbe Ausfallrate haben (Annahmen wie in Beispiel 10.2). Legen Sie das folgende Markoff-Modell zu Grunde. Gehen Sie zur Vereinfachung der Rechnung von der Annahme aus, dass die Reparaturrate wesentlich größer als die Ausfallraten ist. Stellen Sie den Zusammenhang mit dem Resultat vom Ende des Abschnitts 10.3 her.

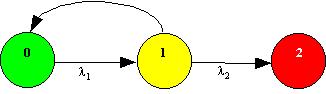
10.10 Gegenstand der Betrachtung ist ein einfaches System, das mit der Ausfallrate l ausfällt. Das System ist reparierbar und die Reparaturrate ist gleich m. Das Markoff-Modell des Systems finden Sie unter dem Text. Anfangs sei das System intakt: p0(0)=1. Gesucht ist die zeitabhängige (!) Unverfügbarkeit des Systems. Stellen Sie die Differentialgleichung auf und finden Sie die Lösung des Anfangswertproblems. Ermitteln Sie die stationäre Unverfügbarkeit und überprüfen Sie dieses Ergebnis.

10.11 Wir betrachten den Abschnitt eines Rohrleitungssystems, das die Fehlfunktion eines der vier Ventile sowohl hinsichtlich des Öffnens als auch hinsichtlich des Schließens toleriert (siehe das untenstehende P&I-Diagramm). Die vier Ventile sind anfangs geschlossen. Nun soll der Abschnitt geöffnet werden. Die Wahrscheinlichkeit dafür, dass ein Ventil nicht öffnet, ist gleich p. Wie groß ist die Versagenswahrscheinlichkeit - also die Wahrscheinlichkeit, dass tatsächlich nicht geöffnet wird? Gehen Sie in folgenden Schritten vor:

  • Aufstellen des Fehlerbaums
  • Formulierung der Indikatorfunktion für das unerwünschte Ereignis
  • Eliminierung der booleschen Operatoren
  • Ermittlung des Erwartungswertes des unerwünschten Ereignisses
  • Setzen Sie p = 0.004 ein.

 

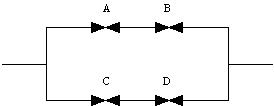
10.12 Gegeben sei ein einfaches parallelredundantes System (1-aus-2-System). Das System gilt als ausgefallen, wenn beide Subsysteme ausgefallen sind (sicherheitsbezogender Ausfall). Für jedes der Subsysteme wird der Ausfall- und Reparaturprozess durch das Markoff-Modell aus Aufgabe 10.10 beschrieben. Die Komponenten mögen eine MTBF von 10 a und eine MTTR von 0.1 a haben. Bestimmen Sie die zeitabhängige sicherheitsbezogene Unverfügbarkeit des 1-aus-2-Systems. Skizzieren Sie das Übergangsverhalten. Ermitteln Sie dazu die Tangente im Nullpunkt und den stationären Wert.

11 Zuverlässigkeitswachstumsmodelle

11.1 Eine vorläufige Zuverlässigkeitsbewertung eines elektronischen Systems ergab 11 Ausfälle in 600 Stunden. Für den endgültigen Betrieb wird ein mittlerer Ausfallabstand von wenigstens 500 Stunden gefordert. Welche Zeit ist für die Test und Nachbesserungsphase noch einzuplanen, wenn der Parameter im Duane-Modell a = 0,3 ist? Was ergibt sich für a = 0,5?

11.2* Analysieren Sie die den Datensatz SYS2 von Musa mit Zuverlässigkeitswachstumsmodellen. Was lässt sich über den Prozess sagen, der diese Daten hervorgebracht hat? Wie wirksam sind die zuverlässigkeitserhöhenden Maßnahmen?

12 Risiko

12.1* Führen Sie die Analyse einer Entscheidung bei Risiko für das Zwei-Turbinen-Kraftwerk mittels Tabellenkalkulation durch. Berechnen Sie die Risiken verschiedener Schalthandlungen wie Ventil öffnen oder schließen. Der Entscheidungsbaum wird nach folgender Transformationsregel direkt aus dem Fehlerbaum der Anlage ermittelt: Eine Bedienhandlung, die eine Komponente in einen falschen (nichtspezifikationsgemäßen) Zustand versetzt, hat dieselben Auswirkungen (Impact) auf das System wie ein gleichartiger Ausfall dieser Komponente. Schreiben Sie ein einfaches Programm mit grafischer Bedienoberfläche. Die Bedienoberfläche enthält Elemente für die Eingabe der Schalthandlungen und für die Anzeige des jeweiligen Risikos.

12.2 Beantworten Sie die folgenden Fragen und begründen Sie kurz Ihre Antworten.

  • Was macht es so schwer, für eine neue Technik ein Grenzrisiko zu definieren, das von der Gesellschaft insgesamt akzeptiert wird?
  • Sie stehen vor der Wahl: Sie bringen vor dem Urlaub ihren Wagen zur Inspektion oder aber nicht. Die Inspektion ist für Sie mit einem Zusatzaufwand von 150 € verbunden. Für eine Panne während des Urlaubs veranschlagen Sie Kosten von 1000 €. Ohne Inspektion werden Sie mit der Wahrscheinlichkeit von 30 % von der Panne getroffen, mit Inspektion beträgt die Pannenwahrscheinlichkeit 10 %. Wie entscheiden Sie?

Zurück zur Seite "Zuverlässigkeit und Sicherheit" 

© Timm Grams, 9. Januar 2008