DENKFALLEN UND PARADOXA

Buch zum Thema:
  

Übersicht

Zu meiner Sammlung der Probleme, Denkfallen und Paradoxa gehören die statistischen Paradoxa von

Was ist eine Denkfalle und was lässt sich dagegen tun?

Eine Denkfalle tut sich auf, wenn eine Problemsituation einen bewährten Denkmechanismus in Gang setzt, und wenn dieser Denkmechanismus mit der Situation nicht zurechtkommt und zu Irrtümern führt.

Denkfallen bewirken kognitive Täuschungen. Sie sind die Quellen von riskanten Manövern, Fehldiagnosen, Design-, Programmier- und Bedienfehlern.

Denkfallen geben sich im Allgemeinen nicht zu erkennen, und man fällt fast zwangsläufig auf sie herein. Aber ist der Argwohn erst einmal geweckt, lässt sich der Reinfall vermeiden. So wie man den optischen Täuschungen beispielsweise durch Anlegen eines Lineals entgehen kann, so lassen sich Denkfallen mittels Logik, Mathematik und Kreativitätstechniken umgehen. Wer sich wappnen will, muss Warnzeichen erkennen und richtig deuten lernen. Deshalb lohnt sich das Studium von Denkfallen.

Klassiker

Was für den einen logisch widersinnig, also paradox ist, das ist für einen anderen eine einfache Denkübung oder gar eine Trivialität. Es kommt immer auf die logischen  und mathematischen Fertigkeiten an und darauf, wie weit man in der Kunst der Modellbildung schon vorangeschritten ist.

Heute wundern wir uns, dass die Menschen bei Zenons Paradoxien – beispielsweise dem Pfeilparadoxon oder dem Paradoxon von Achilles und der Schildkröte – ins Grübeln kommen konnten. Auch Kants Antinomien und Hegels Einlassungen dazu erscheinen uns im Lichte der modernen Naturwissenschaft und Mathematik nur als Konsequenzen ungeeigneter Modellbildung und verquerer Logik. „Dies  Logik zu nennen, kommt mir vor, wie wenn jemand, um eine Bergtour zu machen, ein so langes und faltenreiches Gewand anzöge, dass sich darin seine Füße fortwährend verwickelten und er schon bei den ersten Schritten in der Ebene hinfiele“ meint Ludwig Boltzmann dazu (auf einem Kongress in St. Louis 1904).

Aber hüten wir uns vor Selbstgefälligkeit: „Es ist allerdings nichts Ungewöhnliches, dass Leute eine Paradoxie als trivial ansehen, sobald sie glauben, eine eindeutige Lösung gefunden zu haben. Die Heilung von dieser Reaktion besteht in dem Versuch, jemand anderen von der eigenen ‚Lösung’ zu überzeugen“ (Sainsbury, 1993).

Hintergründe

Mit dem Vortrag „Denkfallen – Klug irren will gelernt sein“ führe ich in die „Philosophie“ dieser Seite ein. Das System der Denkfallen zeigt, welche Mechanismen hinter den Denkfallen stecken. Verwandt mit den Denkfallen und den kognitiven Täuschungen sind die optischen Täuschungen. Die Verführungskraft der Bilder ist Gegenstand der unsortierten Gedanken über die Macht der Bilder. Welche Rolle die Denkfallen beim Zustandekommen von Programmier- und Bedienfehlern spielen, habe ich in einigen Veröffentlichungen beschrieben. Seit März 2011 erfasse ich im Weblogbuch Hoppla! sonderbare Nachrichten und alltäglichen Statistikplunder.

Timm Grams

Simpsons Paradoxon (Simpson’s Paradox)

In der Tabelle der Sterblichkeit aufgrund von Tuberkulose in New York und Richmond aus dem Jahre 1910 begegnet uns das Simpsonsche Paradoxon (Székely, 1990, S. 63, 75 u. 133):

 

Bevölkerung

Todesfälle

Sterberate

 

New York

Richmond

New York

Richmond

New York

Richmond

Weiß

4 675 174

80 895

8 365

131

0,00179

0,00162

Farbig

91 709

46 733

513

155

0,00560

0,00332

Gesamt

4 766 883

127 628

8 878

286

0,00186

0,00224

Widerspruch. Bist du weiß, gehe nach Richmond. Bist du farbig, gehe ebenfalls nach Richmond. Bist du weiß oder farbig, dann bleibe in New York.

Analyse. Statistiken muss man nicht fälschen, wenn man damit irreführen will. Es reicht manchmal schon das Aggregieren von Zähldaten, so wie hier. Etwas durchsichtiger wird der Mechanismus dieser Aggregierungsfalle im Xenophobie-Beispiel. Die Studie Simpson.pdf zeigt, wie man dem Paradoxon nicht nur mit formalen, sondern auch mit grafischen Mitteln beikommen kann.

(1998, 12.07.2010)

Zurück zur Übersicht

Benford's Law

Der Mathematiker Mark Nigrini hat ein Programm geschrieben, mit dessen Hilfe gefälschte Steuererklärungen ausfindig zu machen sind. Es nutzt die Tatsache aus, dass in natürlich vorkommenden Zahlen die Anfangsziffern eine bestimmte markante Verteilung haben. Gefälschte Zahlen weichen davon normalerweise deutlich ab.

Täglich treffen wir auf Zahlen: Zahlen, die auf der ersten Seite einer Tageszeitung stehen, Zahlen über die Größe der Binnengewässer Deutschlands, die Einwohnerzahlen der Städte oder die Familieneinkommen, die Guthaben auf den Konten einer Bank und die Zahlen in einer Steuererklärung. Fragt man nach der Wahrscheinlichkeit, mit der eine beliebig herausgegriffene Zahl mit einer 1 beginnt, werden die meisten Leute antworten: „Die Wahrscheinlichkeit beträgt 1/9.“ Sie gehen davon aus, dass alle Ziffern von 1 bis 9 gleich wahrscheinlich sind (vorausgesetzt, sie haben daran gedacht, dass Nullen praktisch nie am Anfang von Zahlen stehen).

Widerspruch. Schaut man sich die Verteilung der führenden Ziffern bei den Flächen der Länder dieser Erde einmal an, ergibt sich ein anderes Bild: In etwa 30% der Fälle fängt die Zahl mit einer Eins an. Ein ähnliches Bild ergibt sich bei den Einwohnerzahlen und beim Bruttosozialprodukt pro Kopf. Dahinter steckt eine Gesetzmäßigkeit: In einem verblüffend weiten Bereich gilt das Benfordsche Gesetz (Székely, 1990, S. 189).

In der folgenden Grafik ist die Verteilung der führenden Ziffern gemäß diesem Gesetz eingetragen und im Vergleich dazu die sich nach dem Jahrbuch Aktuell 2000 ergebenden Verteilungen der führenden Ziffern statistischer Kennzahlen der 192 selbständigen Länder der Erde.

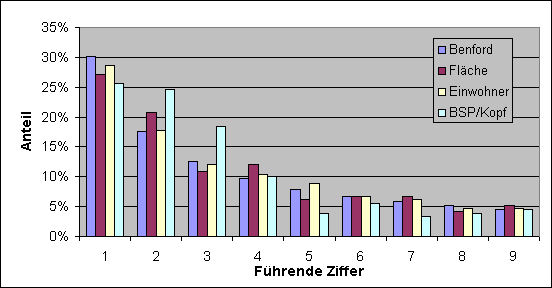
Benfordsches Gesetz

Das Benfordsche Gesetz. Die Wahrscheinlichkeit p(d) dafür, dass eine Zahl mit der Ziffer d beginnt, ist gegeben durch p(d) = ln(1+1/d)/ln(b). Hierin ist b die Basis des Stellenwertsystems für die Zahlendarstellung. Im Dezimalsystems ist b = 10 und das Benfordsche Gesetz vereinfacht sich zu p(d)=log(1+1/d). Darin bezeichnet log den dekadischen Logarithmus.

Analyse. Das Benfordsche Gesetz beschreibt einen empirischen Sachverhalt. In der Literatur findet man aber auch Begründungen. Diese gehen von bestimmten Annahmen über die Statistiken aus und leiten davon das Gesetz ab. Ich mache mir das Gesetz folgendermaßen klar: Viele zahlenmäßig erfassbare Phänomene werden zumindest zeitweise durch exponentielles Wachstum (oder exponentielle Schrumpfung) regiert. Ein Beispiel ist das Wachstum von Guthaben auf einem Bankkonto (Zinseszinsrechnung). Die zu messende Zahl x wächst also exponentiell mit der Zeit t. Das heißt: In gleichen Zeitabschnitten wird immer derselbe prozentuale Zuwachs erzielt. Bis eine führende 1 von der 2 abgelöst wird, muss sich der Wert x verdoppeln. Bis die 2 von der 3 abgelöst wird, muss die Zahl nur noch 50% zulegen. Dementsprechend verringert sich der dafür nötige Zeitraum. Allgemein gilt: Die Zahlen mit einer bestimmten Stellenzahl, die mit der Ziffer d beginnen, beschreiben einen Wertezuwachs um den Bruchteil 1/d. Eine einfache Rechnung zeigt, dass die x-Werte mit der Ziffer d an erster Stelle auf der Zeitachse einen Anteil von ln(1+1/d)/ln(b) ausmachen. Wenn man zu einem Zufallszeitpunkt auf den Prozess trifft, wird demnach die Wahrscheinlichkeitsverteilung für die erste Ziffer dem Benfordschen Gesetz genügen.

Wer weitere Erklärungen sucht, kann beispielsweise bei Kevin Brown und Eric Weisstein nachsehen.

(16. April 1999, 25. April 2000)

Zurück zur Übersicht

 

Xenophobie

Im Städtchen Falldala mit 20 000 Einwohnern beträgt der Ausländeranteil 30 %. Die folgende Tabelle gibt die Kriminalitätsstatistik wieder. Daraus lässt sich folgern: Ausländer neigen stärker zur Kriminalität als Inländer.

Kriminalitätsstatistik von Falldala

 

Einwohner

Straftaten je Jahr

bezogen auf je 1000 Einwohner

Ausländer

6000

51

8.5

Inländer

14000

59

4.2

Widerspruch. Bei eingehender Betrachtung der Kriminalitätsstatistik erweist sich, dass in einem Stadtteil - nennen wir ihn Aschental - die Kriminalität besonders hoch ist. Nun sind, aufgrund der für Inländer unattraktiven Bebauung aus den 50-er Jahren, vorwiegend Ausländer im Aschental angesiedelt. 5 000 der insgesamt 10 000 Bewohner sind Ausländer. Die übrigen leben in der Innenstadt. Die aufgeschlüsselte Statistik sieht folgendermaßen aus:

Kriminalitätsstatistik von Aschental

 

Einwohner

Straftaten je Jahr

bezogen auf je 1000 Einwohner

Ausländer

5000

50

10

Inländer

5000

50

10

Kriminalitätsstatistik der Innenstadt von Falldala

 

Einwohner

Straftaten je Jahr

bezogen auf je 1000 Einwohner

Ausländer

1000

1

1

Inländer

9000

9

1

Es erweist sich, dass die Ausländer nicht häufiger oder weniger häufig zu Straftaten neigen als Inländer. Die anfängliche Vermutung zur Ausländerkriminalität entpuppt sich als zu oberflächlich. Die genauere Betrachtung legt ganz andere Deutungen nahe: Vielleicht liegt es an der Umwelt, an der Armut, am Milieu des Stadtteils. Jedenfalls sind tiefer liegende Analysen erforderlich.

Analyse.: Es handelt sich um eine Aggregierungsfalle wie bei Simpsons Paradoxon. Durch Aggregierung von Zähldaten kommt es zur Blickverengung – die Grundgesamtheit gerät aus dem Blickfeld (Scheinwerferprinzip). Das unspezifische Aggregieren von Zähldaten erzeugt Zusammenhänge, die in der aufgeschlüsselten Statistik nicht existieren. Hier ist es ein Zusammenhang zwischen den Attributen „Ausländer“ und „Neigung zur Kriminalität“.

Darüber hinaus wird der statistische Zusammenhang unzulässigerweise im Sinne eines Kausalzusammenhangs interpretiert: Wer Ausländer ist, neigt stärker zu kriminellen Handlungen als ein Inländer. Das ist eine Denkfalle, die auf die Kausalitätserwartung - einen angeborenen Lehrmeister (Konrad Lorenz) also - zurückgeht. Dass viele Menschen an Astrologie glauben, könnte an demselben Denkmuster liegen, wie mehreren Beiträgen im Spektrum der Wissenschaft zu entnehmen ist (Michael Springer, 4/1999, S. 106; Gunter Sachs, 7/1999, S. 9; Herbert Basler, 8/1999, S. 94 ff.).

(6.9.1999)

Zurück zur Übersicht

Wasons Auswahlaufgabe (Wason’s Selection Task)

Die abgebildeten vier Karten ent­hal­ten jeweils auf einer Seite einen Buchstaben und auf der anderen eine Zahl.

Welche Karten muss man notwendigerweise umdrehen, wenn man feststellen will, ob folgende Aussage gilt: "Wenn auf einer Seite der Karte ein Vokal abgebildet ist, dann steht auf der anderen Seite eine gerade Zahl"?

Widerspruch. In einem psychologischen Experiment wählten die meisten Versuchspersonen die Karten mit dem E und die mit der 4. Dabei bringt es gar nichts, die Karte mit der 4 umzu­drehen! Welcher Buchstabe auch immer auf der Rückseite steht: er passt zur zu prüfenden Aussage. Nur durch Umdrehen der Karten mit dem E und der 7 haben wir eine Chance, die Aussage zu widerlegen. Diese Möglichkeit wählte nur eine Minderheit von 4 % der Befragten.

Analyse. Unsere Anlage zur Induktion, also die Fähigkeit, Erweiterungsschlüsse zu ziehen und Theorien zu bilden, arbeitet nach folgendem Argumentationsmuster: Wenn sich aus der Theorie (Hypothese) H ein Ereignis E vorhersagen lässt, und wenn gleich­zei­tig das Ereignis E aufgrund des bisherigen Wissens recht un­wahr­schein­lich ist, dann wird die Theorie H aufgrund einer Beobachtung des Ereignisses E glaub­wür­diger. Kurz: Aus „H impliziert E“ und „E ist wahr“ folgt „H wird glaub­wür­di­ger“. Wir tendieren dazu, diese plausible Schlussfolgerung (Induktionsschluss) mit größerer Bestimmtheit anzureichern: Aus „H impliziert E“ und „E ist wahr“ meinen wir auf „H ist wahr“ schließen zu können; aber das ist ein unerlaubter Umkehrschluss. Diese Denkfalle wird auch als Schei­tern am Modus Tollens bezeichnet (Anderson, 1988, S. 248). Die Induktions-Denkfalle schlägt  in Wasons Auswahlaufgabe sogar zweimal zu:

1.      Da die Theorie H durch ein korrekt vorhergesagtes Ereignis E glaubwürdiger wird, su­chen wir nach genau solchen Ereignissen. Diese Bestätigungssucht ist ein unvermeidlicher Begleiter unserer Anlage zur Induktion. Sie verleitet uns dazu, die Karte mit der 4 umzudrehen. Gerade der Wissenschaftler läuft Gefahr, der Bestätigungssucht zu erliegen: Die von ihm aufgestellte und geliebte Theorie soll sich ja bewähren und nicht etwa als unnütz oder falsch herausstellen.

2.      Die Theorie H ist selbst als Implikation formuliert: Aus „Auf der Karte steht ein Vokal“ folgt „Auf der Karte steht eine gerade Zahl“. Der gern gezogene aber unerlaubte Umkehrschluss sieht so aus: Aus „Auf der Karte steht eine gerade Zahl“ folgt „Auf der Karte steht ein Vokal“. In diesem Licht ist dann auch die Auswahl der Karte mit der 4 vernünftig. Durch den unerlaubten Umkehrschluss erscheint die Theorie als strenger als sie ist. In dieser strengeren Fassung könnte sie sogar durch die Karte mit dem K widerlegt werden, beispielsweise dann, wenn auf der Rückseite eine 2 stünde.

Wollte man eine Theorie auf dem Weg der Bestätigung beweisen, müsste man alle ihre Vorhersagen überprüfen – nicht nur einige der richtigen. Bei wissenschaftlichen Theorien mit ihren weit reichenden Aussagen ist das ein aussichtloses Unterfangen. Dagegen lassen sich Theorien durch Aufzeigen eines einzigen Gegenbeispiels widerlegen (falsifizieren). Diese Chance bieten in unserem Fall nur die Karte mit dem E und die mit der 7. Auch wenn wir nicht nach Widerlegungen suchen: Wir sehen sie schnell ein. Wir verhalten uns wie „pas­sive Pop­peria­ner“, sagt Evans (1989).

(05.11.05)

Zurück zur Übersicht

Die Harvard-Medical-School-Studie

Wir betrachten einen Test für eine Krankheit, die die Basisrate 1/1000 besitzt - also: Einer unter eintausend Menschen ist krank. Der Test liefert mit der Wahrscheinlichkeit von 5% ein falsches Ergebnis. Insbesondere hat er eine Falsch-positiv-Rate von 5%. Wie hoch ist die Wahrscheinlichkeit, dass eine Person mit einem positiven Testergebnis tatsächlich die Krankheit hat?

Widerspruch. Das häufigste Urteil von Professoren, Ärzten und Studenten ist „95%“. Die Analyse zeigt aber, dass die Wahrscheinlichkeit tatsächlich unter 2% liegt. Der folgende Balken möge eintausend Personen repräsentieren. Von den tausend Personen ist (im Durchschnitt) eine wirklich krank. Sie wird durch das dunkle Feld ganz links repräsentiert. Bei etwa 50 Personen ist der Test falsch-positiv. Von den 51 Personen mit positivem Test ist also nur eine wirklich krank, was einem Anteil von weniger als 2% entspricht (Hell/Fiedler/Gigerenzer, 1993).

1

50

949

 Analyse: Der hier beobachtete Fehlschluss ist eine stochastische Variante von logischen Fehlschlüssen der folgenden Art: Aus den Sätzen „Wenn es regnet wird die Erde nass“ und „Die Erde ist nass“ schließen wir - fälschlich - auf „Es hat geregnet“. Das ist das gelegentliche Scheitern am Modus Tollens (Anderson, 1988, S. 248 ff.). Wir schließen also von der Wirkung auf die Ursache. Aber bestenfalls können wir die Ursache aufgrund der beobachteten Wirkung als plausibler ansehen - keineswegs jedoch als zwingend. Bei der Harvard-Medical-School Studie ist es die Krankheit, die wir als Ursache des positiven Testergebnisses ansehen. Auch hier wird ein bestenfalls plausibler Rückschluss als zwingend überinterpretiert. Die systematische und krasse Fehlschätzung beruht auf einer Überbewertung bestätigender Informationen.

Wer mehr über statistische Irrtümern aller Art und deren „Überwältigung“ lesen will, findet das in vergnüglicher Form im Buch von Beck-Bornholdt und Dubben (2001).

(22.12.1999)

Zurück zur Übersicht

Software-Verifikation und -Test

In einem Lehrbuch zum Thema Zuverlässigkeitsnachweis von Software finde ich den fett hervorgehobenen Satz: „Der Test von Hypothesen geht über die Falsifizierung ihres Komplements“ (Ehrenberger, 2002, S. 116).  Dann wird gezeigt, dass bei einem Sachverhalt, der nicht der Hypothese entspricht, der Test schlimmstenfalls mit einer geringen Wahrscheinlichkeit (von sagen wir 5%) bestanden wird. Aus dem Bestehen des Tests wird dann gefolgert, dass das Komplement unwahrscheinlich ist (5%) und die Hypothese entsprechend wahrscheinlich (95%).

Widerspruch. Zwei Fehler stecken in dem „Beweis“. Erstens wird durch ein negatives Testergebnis („bestanden“) nicht das Komplement der Hypothese falsifiziert, sondern ein ganz bestimmter Sachverhalt, die Alternativhypothese nämlich. Eine Widerlegung der Alternativhypothese allein zeigt noch nicht, dass die Hypothese wahr ist. Zweitens wird eine Wahrscheinlichkeitsaussage über Testergebnisse als Wahrscheinlichkeitsaussage über die Hypothesen genommen. Und dafür fehlt jegliche Begründung. Man hat ja bei der Berechnung der Wahrscheinlichkeiten die Alternativhypothese als fest gegeben vorausgesetzt. Die Wahrscheinlichkeiten sind demzufolge bedingte Wahrscheinlichkeiten. Dem Gedankengebäude fehlt das mathematisch-logische Fundament, es ist auf Sand gebaut.

Analyse (mit etwas mehr Mathematik als sonst). Zu den Fehlern tragen Denkmechanismen bei, die bereits in Wasons Auswahlaufgabe und in der Harvard-Medical-School-Studie eine Rolle gespielt haben. Um die Sache klarer zu machen, schließe ich an die dort bereits eingeführte mathematische Notation an. In der Testtheorie wird die ursprüngliche Hypothese als Nullhypothese bezeichnet, kurz H0. Das Komplement bezeichne ich hier einmal mit ¬H0 (gesprochen: „nicht H null“). Es gilt entweder H0 oder ¬H0. Die Alternativhypothese H1 ist ein bestimmter mit der Hypothese unverträglicher Sachverhalt. Es gilt demnach: H1 impliziert ¬H0. Der erste Fehlschluss geht auf unsere Anlage zur Induktion zurück, auf das plausible Schließen anstelle der hier erforderlichen exakten Deduktion: Von der Widerlegung der Alternativhypothese, von ¬H1 also, meint man auf  H0 schließen zu können. Das ist ein Irrtum. Nun zum zweiten Fehlschluss: E bezeichne die Beobachtung, dass der Test bestanden worden ist. Ausgangspunkt des „Beweises“ ist die Feststellung, dass der Test bei Vorliegen der Alternativhypothese mit einer Wahrscheinlichkeit von nur 5% bestanden wird: p(E |H1) = 5%. Daraus wird dann gefolgert, dass die Alternativhypothese bei Bestehen des Tests mit nur 5-prozentiger Wahrscheinlichkeit wahr sein kann: p(H1 |E) = 5%. Das ist ein unerlaubter Umkehrschluss, ein weiterer Induktionsfehler also. Zwar lässt sich die Wahrscheinlichkeit  p(H1 |E) mit der Formel von Bayes ermitteln. Spätestens im Zuge der Berechnung wird erkennbar, dass zusätzliche Daten erforderlich sind. Man braucht die A-priori-Wahrscheinlichkeiten der Hypothesen, bevor man etwas über die Auswirkungen des Tests sagen kann. Und von solchen Aprioris ist in dem angesprochenen „Beweis“ nirgends die Rede. (Zu den Hintergründen dieses Beispiels: Des Ingenieurs Schwierigkeiten mit der schließenden Statistik.)

Zusatz. Schlecht fundierte Theorien sind paradoxerweise im Qualitätswesen nicht gerade selten. Ein Beispiel entdeckte ich kürzlich: die  „exakten“ Formeln von Clopper und Pearson. Diese Formeln zur Abschätzung einer Wahrscheinlichkeit werden immer wieder in den Lehrbüchern referiert, zusammen mit einer ziemlich sonderbaren „Herleitung“. Dabei ist schon lange bekannt, dass die Formeln alles andere als exakt sind. Im Skriptum „Grundlagen des Qualitäts- und Risikomanagements“ kritisiere ich einige der fragwürdigen „Theorien“ aus der Welt der Zuverlässigkeit und Sicherheit: Bayesschätzung kontra Testtheorie, X-Ware Reliability, diversitäre Programmierung (Software-Diversität), Zuverlässigkeitswachstumsmodelle.

(29.05.08)

Zurück zur Übersicht

Bayes-Schätzung

Im Abschnitt über die Harvard-Medical-School-Studie wird mit einer einfachen Häufigkeitsbetrachtung die Wirksamkeit eines diagnostischen Tests abgeschätzt. Durch den Übergang von Häufigkeiten auf Wahrscheinlichkeiten wird daraus die Bayes-Schätzung (Sachs, 1992). Was auf diagnostische Tests so erfolgreich angewendet wird, das sollte auf Parameterschätzungen übertragbar sein. Hierbei geht es nicht mehr um die Abschätzung, ob eine bestimmte Krankheit vorliegt oder nicht, sondern um die Abschätzung einer Einflussgröße (Parameter), die nicht direkt messbar ist. Beispiel für einen solchen Parameter ist die Fehlerwahrscheinlichkeit eines Produkts, das unter bestimmten Bedingungen in Serie gefertigt wird. Die Fehlerwahrscheinlichkeit ist nicht bekannt. Aber man kann sich eine Stichprobe des Produkts verschaffen und den Anteil der fehlerhaften Exemplare feststellen. Wie beim diagnostischen Test soll aus dem beobachteten Ergebnis (Testergebnis bzw. Fehleranteil) eine Wahrscheinlichkeitsaussage über den eigentlich interessierenden Sachverhalt (Krankheit bzw. Fehlerwahrscheinlichkeit) abgeleitet werden. In beiden Fällen geht es also um die Wahrscheinlichkeiten von Hypothesen, einmal um Hypothesen über eine Krankheit und das andermal um Hypothesen über mögliche Fehlerwahrscheinlichkeiten. In beiden Fällen braucht man eine Anfangsschätzung. Beim diagnostischen Test ist das die Basisrate der Krankheit. Bei der Parameterschätzung geht man von einer mehr oder weniger willkürlichen Schätzung der Hypothesenwahrscheinlichkeiten aus (A-priori-Wahrscheinlichkeiten). Durch Anwendung der Formel von Bayes wird diese Schätzung unter Einrechnung der gemachten Beobachtung verbessert (A-posteriori-Wahrscheinlichkeiten).

Widerspruch. Die Anwendung der Formel von Bayes auf Parameterschätzungen kann zu paradoxen Ergebnissen führen. Es gibt Fälle, in denen die Schätzung immer schlechter wird, je mehr Daten man berücksichtigt.

Analyse. Im Kern besagt die Formel von Bayes, dass die Wahrscheinlichkeit einer Hypothese H („Person ist krank“) durch die gemachte Beobachtung E („Test ist positiv“) in demselben Verhältnis steigt, wie die Beobachtung durch die Hypothese wahrscheinlicher wird. Mit den Formelzeichen für (bedingte) Wahrscheinlichkeiten sieht dieser Zusammenhang so aus: P(H|E)/P(H) = P(E|H)/P(E). Im Fall der Harvard-Medical-School-Studie setzen wir folgende Daten als bekannt voraus: P(H)=0,1%, P(E|H)=95% (Sensitivität des Tests), P(E)≈5,1%. Die Formel liefert dann das Ergebnis: Eine positiv getestete Person ist mit der Wahrscheinlichkeit von weniger als 2% tatsächlich krank. Diese Anwendung der Bayes-Formel auf diagnostische Tests ist methodisch einwandfrei. Die Wahrscheinlichkeiten P(H) und P(H|E) sind die A-priori- bzw. A-posteriori-Wahrscheinlichkeit der Hypothese.

Dass die Sache bei der Parameterschätzung zuweilen nicht so richtig funktioniert, wird in der Literatur auf zwei Ursachen zurückgeführt (Fisz, 1976, S. 580; Papoulis, 1965, S. 114):

1.      Man braucht eine Anfangsschätzung der Verteilung des Parameters. Und über dieses Apriori ist meist nichts bekannt; es wird willkürlich angesetzt.

2.      Da der abzuschätzende Parameter im Allgemeinen eine zwar unbekannte aber immerhin feste Größe ist, darf man ihn eigentlich nicht als Zufallsvariable betrachten. Die Schlussfolgerungen aus der Bayes-Formel sind in diesem Sinne praxisfern.

Diese Einwände sind aus mathematischer Sicht eher harmlos. Sie allein können die paradoxen Ergebnisse nicht erklären. Ich sehe einen weiteren Grund für das gelegentliche Nichtfunktionieren der Parameterschätzung mit dem Bayes-Verfahren.

3.      Die A-posteriori-Verteilung des Parameters wird zuweilen falsch interpretiert. Sie wird – gegenüber der A-priori-Verteilung – als bessere Schätzung der tatsächlichen Verteilung des Parameters angesehen. Die A-posteriori-Verteilung ist aber nur eine verbesserte Schätzung unter der Bedingung der gemachten Beobachtung. Mit anderen Worten: Die Verteilung besagt, mit welchen Wahrscheinlichkeiten die verschiedenen Parameterwerte zu dem beobachteten Ergebnis beigetragen haben könnten. Der Umkehrschluss von der Beobachtung auf die nicht bedingte Hypothese ist allenfalls plausibel, es handelt sich um einen Induktionschluss. Es kommt zum Fehler, wenn aus einer Beobachtung zu starke Schlussfolgerungen gezogen werden.

In der medizinischen Diagnostik nimmt man die A-posteriori-Wahrscheinlichkeit tatsächlich nicht als eine verbesserte Wahrscheinlichkeitsschätzung gegenüber dem Apriori: Die Basisrate der Krankheit bleibt unverändert. Die errechnete A-posteriori-Krankheitswahrscheinlichkeit gilt nur für die Personen mit positivem Testergebnis und nicht etwa für „die ganze Welt“. Mit einem einfachen Beispiel will ich diesen dritten Punkt veranschaulichen.

Tabelle der Wahrscheinlichkeiten aller Kombinationen

Auszahlung E
(Messergebnis)

Hypothesen über die
Anzahl der Münzen im Spiel

Zeilen­summe

H1

H2

H3

0

4/24

2/24

1/24

7/24

1

4/24

4/24

3/24

11/24

2

0

2/24

3/24

5/24

3

0

0

1/24

1/24

Spaltensumme

1/3

1/3

1/3

1

Das Ein-Euro-Spiel. Sie bekommen angeboten, für einen Euro Einsatz an folgendem Spiel teilzunehmen. Im Verborgenen werden durch Zufallsauswahl eine, zwei oder drei Münzen ausgewählt und dann geworfen. Für jede Münze, die Kopf zeigt, wird ein Euro ausgezahlt. Sie wollen wissen, ob sich das Spiel für Sie lohnt. Aus den Wahrscheinlichkeiten für die Wahl einer, zweier oder dreier Münzen, und unter der Voraussetzung, dass es sich um faire Münzen handelt (je 50% Wahrscheinlichkeit für Kopf und Zahl), wollen Sie die Gewinnerwartung  ermitteln. Das Dumme ist nur: Sie kennen die Verteilung des Parameters „Anzahl der Münzen“ nicht. Sie schauen dem Spiel eine Weile zu und wollen aus den beobachteten Auszahlungen und unter Zuhilfenahme der bayesschen Formel eine möglichst gute Schätzung dieser Verteilung herausfinden. Sie nennen die Hypothesen, dass 1, 2 oder 3 Münzen geworfen werden, H1, H2 und H3. Als Anfangsschätzung nehmen Sie – nach dem Indifferenzprinzip – die Gleichverteilung an: P(H1) = P(H2) = P(H3) = 1/3. In einer Tabelle stellen Sie die sich daraus ergebenden Wahrscheinlichkeiten für alle möglichen Ereignisse (Kombinationen von Münzzahl und Auszahlung) zusammen.

Nun machen Sie die Beobachtung E: Es wird ein Euro ausgezahlt. Die bayessche Formel liefert Ihnen die A-posteriori-Wahr­schein­lich­kei­ten der Hypothesen:

P(H1|E) = P(H1)∙P(E|H1)/P(E) = P(EH1)/P(E) = (4/24)/(11/24) = 4/11,

P(H2|E) = 4/11,

P(H3|E) = 3/11.

Das lässt, unter Berücksichtigung der Anfangsverteilung des Parameters, den Schluss zu, dass an dem konkreten Spielergebnis (nämlich ein Euro Auszahlung) mit der Wahrscheinlichkeit 4/11 nur eine Münze im Spiel war; mit derselben Wahrscheinlichkeit waren es zwei Münzen und mit der Wahrscheinlichkeit 3/11 waren es drei Münzen. Dementsprechend korrigieren Sie Ihre Schätzung der Hypothesenwahrscheinlichkeiten.

Seien Sie gewarnt. Die Neubewertung der Hypothesen durch die A-posteriori-Wahrscheinlichkeiten lässt sich vielleicht manchmal aus pragmatischer Sicht rechtfertigen, mathematisch begründbar ist sie nicht. Und sie kann absurde Ergebnisse liefern. Und das ist in diesem Spiel der Fall. Beispielsweise würde eine Auszahlung von drei Euro zu der endgültigen Einschätzung führen, dass grundsätzlich drei Münzen im Spiel sind. Dann säßen Sie in der Falle und liefen Gefahr, die Gewinnerwartung zu hoch einzuschätzen.

Anders sieht die Sache aus, wenn der „Spielautomat“ immer für einen ganzen Tag – also über viele Spiele – bei seiner Münzenauswahl bleibt. In diesem Fall funktioniert Ihre Bayes-Schätzung und Sie können daraufhin für den Tag entscheiden, ob Sie mitmachen wollen oder nicht.

(10.09.2008)

Zurück zur Übersicht

Umtauschparadoxon (Briefumschlag-Paradoxon)

Zwei Briefumschläge enthalten Geld, einer doppelt so viel wie der andere. Ich darf einen Umschlag auswählen, und das Geld entnehmen. Danach darf ich entscheiden, ob ich das Geld behalten will oder zum anderen Kuvert wechsle. Angenommen, ich ziehe ein Kuvert und finde 100 € darin.  Eine kurze Überlegung zeigt mir, dass ich das Angebot zum Umtausch annehmen sollte: Da ich den Briefumschlag rein zufällig gewählt habe, ist die Wahrscheinlichkeit dafür, dass ich zunächst den kleineren Betrag gezogen habe genauso groß wie die Chance für den größeren Betrag, also jeweils gleich ½. Den 100 €, die ich jetzt habe, stehen im Falle des Umtauschs ½ ∙ 200 € plus ½ ∙ 50 € gegenüber. Das ist eine Gewinnerwartung von 125 €, und das sind 25 € mehr als ohne Umtausch.

Widerspruch. Da es auf den Betrag nicht ankommt, hätte ich mich – ohne den Umschlag zu öffnen – gleich für den anderen Briefumschlag entscheiden können. Aber damit bin ich wieder bei der Ausgangssituation: Ich habe ja einfach nur gewählt und kann dieselbe Überlegung wie oben anstellen. Der Wechsel würde auch jetzt Gewinn versprechen, obwohl ich dann wieder beim ersten Umschlag gelandet wäre.

Analyse. Das Paradoxon kommt durch eine unzulässige Anwendung des Indifferenzprinzips (John Maynard Keynes) zustande: „Wenn keine Gründe dafür bekannt sind, um eines von verschiedenen möglichen Ereignissen zu begünstigen, dann sind die Ereignisse als gleich wahrscheinlich anzusehen“ (Rudolf Carnap/Wolfgang Stegmüller; 1959, S. 3). Wahrscheinlichkeiten dafür, dass in den Umschlägen bestimmte Summen stecken, sind zwar denkbar. Aber über die Wahrscheinlichkeiten dieser verschiedenen Fälle ist nichts bekannt. Zu allem Überfluss ist die unterstellte Gleichverteilung aller möglichen Fälle sogar prinzipiell unmöglich: Bei einer potentiell unendlichen Anzahl von Fällen kann nicht jeder der Fälle dieselbe Wahrscheinlichkeit haben. Mit dem Indifferenzprinzip unterstellen wir hier eine Struktur, die tatsächlich nicht vorhanden ist. Das ist eine Überschätzung des Ordnungsgehalts der Dinge in Folge der uns innewoh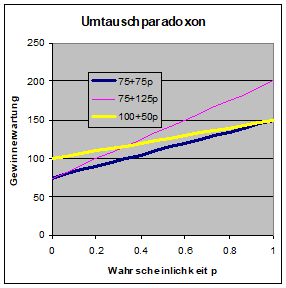nenden Prägnanztendenz.

Zusatz 1. Wir nehmen einmal an, dass nur zwei Fälle zu unterscheiden sind. Die Briefumschläge enthalten im ersten Fall 50 € und 100 € und im zweiten Fall 100 € und 200 €. Die Person, die die Briefumschläge füllt und anbietet,  möge mit der Wahrscheinlichkeit p den Fall 2 realisieren und ansonsten den Fall 1. Gehen wir zunächst einmal davon aus, dass ich über den Inhalt der Umschläge vollständig im Unklaren gelassen werde. Der Inhalt des zunächst gewählten Briefumschlags hat jetzt auf meine Entscheidung keinen Einfluss. Ich kann mich dafür entscheiden, grundsätzlich nicht zu tauschen. Das ergibt eine Gewinnerwartung von  €. Das sind 75+75p €. Denselben Wert erhalte ich, wenn ich mich für die Strategie entscheide, grundsätzlich zu tauschen. Der Tausch verbessert also erwartungsgemäß nichts.

Anders sieht die Sache aus, wenn die Person mich über die möglichen Fälle vorab informiert: Jetzt mache ich meine Entscheidung vom Inhalt des gewählten Umschlags abhängig: Ich tausche immer dann, wenn weniger als 200 € im Umschlag sind. Nun ist meine Gewinnerwartung gleich 75 + 125p €. Diese Strategie zahlt sich aus, solange p größer als 0 ist, also solange überhaupt die Umschläge mit den höheren Beträgen in Frage kommen. Eine weitere Variante besteht darin, nur dann zu wechseln, wenn zunächst nur 50 € gezogen worden sind. Die Gewinnerwartung beträgt jetzt 100 + 50p €. Diese Strategie ist der eben beschriebenen überlegen, solange p < 1/3 ist.

Zusatz 2. Durch die Einbeziehung weiterer Fälle lassen sich diese Überlegungen problemlos verallgemeinern. Sogar (abzählbar) unendlich viele Fälle dürfen es sein. Und auch eine Obergrenze für den Betrag ist keinesfalls zwingend. Man könnte beispielsweise den Fällen 1, 2, 3,  … die Wahrscheinlichkeiten ½, ¼, ⅛, ...  zuordnen. Die Briefumschläge könnten dann 1 € und 2 €, 2 € und 4 €, 3 € und 6 €, … enthalten. Das ist nur eine aus einer unübersehbaren Vielfalt von möglichen Aufteilungen. Die beste Strategie für das Umtauschen hängt davon ab, welche Informationen über die Fälle und deren Wahrscheinlichkeiten verfügbar sind.

Der informierte Mitspieler wird unter den eben beschriebenen Bedingungen immer dann tauschen, wenn er zunächst einen ungeraden Euro-Wert gezogen hat. Ansonsten bleibt er bei seiner ersten Wahl. Er kann auf diese Weise seine Gewinnerwartung um 5/9 € verbessern und erreicht so etwa 3 € und 56 Cent anstelle der 3 € bei „blindem“ Verhalten.

 (02.08.08)

Umtauschparadoxon für Fortgeschrittene

Mein Wohltäter informiert mich, dass er beim Füllen der Umschläge so vorgegangen ist: Anfangs hat er in den einen Umschlag 1 € gelegt und in den anderen 2 €. Dann hat er so lange gewürfelt, bis er die Augenzahl 1 oder 2 erhalten hat. Immer wenn das nicht der Fall war, also bei den Augenzahlen 3, 4, 5 oder 6, hat er die Beträge in den Umschlägen jeweils verdoppelt. Das Ergebnis dieser Prozedur – so sagt der Wohltäter – steckt in den Briefumschlägen.

Ich ziehe einen Umschlag und es sind 16 € drin. Ich überlege: Die Wahrscheinlichkeit des Falles, dass das der kleinere Betrag ist, steht zu der Wahrscheinlichkeit des anderen Falles im Verhältnis 2:3. Den kleineren Betrag habe ich also mit der (bedingten) Wahrscheinlichkeit 2/5 oder 40 % gezogen und den größeren mit der Wahrscheinlichkeit 3/5 oder 60 %. Wenn ich tausche, beträgt der Erwartungswert demnach 16 € multipliziert mit dem Faktor 2∙40 % + ½∙60 %, das sind 110 %. Der Umtausch lässt im Mittel 10 % mehr erwarten als ich in der Hand halte. Das entspricht einem mittleren Zugewinn um 1 € und 60 Cent. Das Risiko, mit 60-prozentiger Wahrscheinlichkeit 8 € zu verlieren, fällt nicht so sehr ins Gewicht. Ich finde: Der Tausch lohnt sich. (Die Zugewinnerwartung von 10 % bei Tausch gilt für jeden gezogenen Wert über 1 €; bei einem Euro ist sie gleich 100 %.)

Widerspruch. Treffe ich die Entscheidung grundsätzlich auf der Basis des zu erwartenden Gewinns, werde ich stets tauschen, egal welchen Betrag ich zunächst gezogen habe. Damit ergibt sich derselbe Widerspruch wie beim einfachen Umtauschparadoxon. Nur dass er sich jetzt nicht mehr so leicht auflösen lässt.

Analyse. Der Nachweis, dass die Tausche-immer-Strategie bei Wiederholung des Spiels und auf lange Sicht der Tausche-nie-Strategie überlegen ist, scheitert daran, dass die jeweiligen Erwartungswerte für die Auszahlungen unendlich groß sind. Tatsächlich ist es so, dass bei subjektiver Bewertung der Gewinnaussichten und der Risiken, ein Tausch immer fraglicher wird, je höher der zunächst gezogene Betrag ist. Das Risikoargument nährt übrigens auch erhebliche Zweifel am Angebot und an der Aufrichtigkeit des Wohltäters, dem ja keine unbegrenzten Finanzmittel zur Verfügung stehen. Wir stehen hier vor ähnlichen Realisierungsschwierigkeiten wie beim Schneeballsystem.

Eine detaillierte Analyse finden Sie in Umtauschparadoxon.pdf. Dazu gibt es eine kleine stochastische Simulation als lauffähiges Java-Archiv (Umtauschparadoxon.jar).

Den Hinweis auf das schwere Umtauschparadoxon habe ich der englischsprachigen Wikipedia entnommen: http://en.wikipedia.org/wiki/Two_envelopes_problem.

(13.07.09)

 Zurück zur Übersicht

 

Halbkreis

Aufgabe. Schätzen Sie ab, wie groß die Wahrscheinlichkeit dafür ist, dass drei rein zufällig und unabhängig voneinander gewählte Punkte eines Kreises auf einem - passend positionierten - Halbkreis liegen?

Widerspruch. Die Wahrscheinlichkeit wird meist unterschätzt - und zwar wird sie unter 50% - manchmal sogar bei 25% und weniger - vermutet. Mittels eines kleinen Experiments können Sie sich überzeugen, dass die Wahrscheinlichkeit wesentlich höher liegt. Sie beträgt genau 75%.

Analyse. Man denkt sich wohl zunächst einen festen Halbkreis und schließt daraus auf eine kleine Wahrscheinlichkeit dafür, dass die drei gewählten Punkte auf diesem Halbkreis liegen. Der Anfangsschätzwert ist also etwa 1/8. Dann dreht man in Gedanken den Halbkreis so, dass möglichst viele der Punkte erfasst werden. Durch die Möglichkeit der Anpassung des Halbkreises an die Position der Punkte muss die Wahrscheinlichkeit wohl größer sein als die Anfangsschätzung. Dementsprechend wird der Schätzwert korrigiert. Diese Korrektur geschieht aber zu vorsichtig (Verankerung): „In many situations, people make estimates by starting from an initial value that is adjusted to yield the final answer... In either case, adjustments are typically insufficient. That is, different starting points yield different estimates, which are biased toward the initial values“ (Tversky, Kahnemann, 1974).

(23.12.99)

Zurück zur Übersicht

Das Braess'sche Paradoxon

In manchen Fällen bewirkt eine Aktion genau das Gegenteil dessen, was damit beabsichtigt ist (Spektrum der Wissenschaft 1992, Heft 11, S. 23-26): Eine zusätzliche Entlastungsstraße macht die Verkehrsstaus schlimmer (Dietrich Braess). Um zu zeigen, wie so etwas passieren kann, habe ich mir das folgende Spiel ausgedacht (es ist eine vereinfachte Version des Verkehrsproblems):

Es handelt sich um ein Zweipersonenspiel. Vorgelegt wird vom Spielleiter die Zeichnung eines Rechtecks. Jeder Spieler hat die Aufgabe, entlang der Kanten dieses Rechtecks einen Weg zu suchen, der ihn von der linken oberen Ecke zur rechten unteren Ecke führt, und zwar zu möglichst geringen Kosten. Die Wegekosten betragen 2 Einheiten für jede der horizontalen und 5 Einheiten für jede der vertikalen Kanten. Wird eine der Kanten von beiden Spielern gewählt, haben sie - wegen gegenseitiger Behinderung - den doppelten Preis zu zahlen. Einer der Spieler wählt seinen Weg „oben herum“ und zahlt die Wegekosten 7 (=2+5). Der andere geht „unten herum“ und zahlt ebenfalls 7 (=5+2) Einheiten.

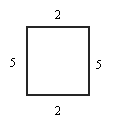
Der Spielleiter eröffnet nun den Spielern die Möglichkeit, ihre Kosten zu senken, indem er eine zusätzliche und kostenlose Verbindung von rechts oben nach links unten einführt. Diese Möglichkeit nutzt einer der Spieler auch tatsächlich aus. Er zahlt nun nur noch 6 (=2+0+2×2) Einheiten. Da eine der Verbindungen von beiden benutzt wird, muss der andere Spieler jetzt mehr zahlen, nämlich 9 (=5+2×2) Einheiten. Das lässt ihm keine Ruhe, und er macht es wie sein Gegenspieler.

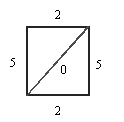
Beide wählen schließlich den z-förmigen Weg und zahlen jeweils 8 (=2×2+2×0+2×2) Einheiten. Obwohl beide jetzt schlechter fahren als zu Beginn, als es die Entlastungsverbindung noch nicht gab, kann jeder der Spieler nur noch zu seinem eigenen Nachteil vom z-förmigen Weg abweichen. In der Spieltheorie nennt man so etwas ein Nash-Gleichgewicht. Übrigens: Es bringt auch nichts, wenn sich beide absprechen und den vorteilhafteren Weg abwechselnd benutzen. Der Mittelwert liegt dann immer noch höher als bei den getrennten Wegen. Aus dieser misslichen Situation kommen beide nur heraus, wenn sie beschließen, den Entlastungspfad zu ignorieren und zu ihren ursprünglichen Wegen zurückkehren. Darin liegt das Paradoxon.

Wir haben es hier mit einer Variante des Gefangenen-Dilemmas zu tun, das ausgiebig in „Die Evolution der Kooperation“ von Robert Axelrod (1987) behandelt wird.

Sehr eindrucksvoll ist ein mechanisches Analogon zum Braess'schen Paradoxon.

(16. April 1999)

Zurück zur Übersicht

Je schlechter, desto besser

Zurzeit kommt bei Lebensmittelkontrollen ziemlich viel Unappetitliches zu Tage (Der Spiegel 48/2005, S. 38-40). Das wird von manchem Politiker als Erfolg gedeutet: Dass man dies alles aufgedeckt habe, spreche doch für die Güte der staatlichen Kontrollen.

Widerspruch. Der Erfolg der Kontrolleure lässt sich kostengünstig verbessern – durch die Entlassung von Kontrolleuren. Bei halb so vielen Kontrolleuren halbiert sich für den skrupellosen Händler das Risiko, erwischt zu werden. Oder anders herum: Bei gleichem Risiko kann er mit noch mehr Sauereien zusätzliches Geld machen. Die Erfolgsquote der verbliebenen Kontrolleure steigt. Die Lage wird schlechter, der Kontroll-Erfolg besser.

Kommentar und Analyse. Heutzutage wird alles Mögliche evaluiert und in Ranking-Listen einsortiert. Diesem Trend gegenüber ist Misstrauen angebracht, denn objektive und manipulationsresistente Maßstäbe sind rar. Das lineare Ursache-Wirkungsdenken und die Überbewertung bestätigender Information sorgen für Blickverengung und für Trugschlüsse. Um beim Beispiel zu bleiben: Jeder aufgedeckte Fall von Lebensmittelbetrug spricht für die Qualität der Kontrolleure, aber eben auch für schlechte Zustände.

Es folgen weitere Beispiele für Je-schlechter-desto-besser-Effekte.

Qualitätsverbesserung durch Selektion. Die Regierung von Irgendwo meldet: „Vor zwei Jahren  hat diese Landesregierung die Aufnahmebedingungen für Gymnasien verschärft. Seither haben sich die durchschnittlichen Leistungen an unseren Gymnasien deutlich verbessert. Die Real- und Hauptschulen haben ebenfalls von der Maßnahme profitiert; auch an diesen Schulen sind die Noten im Durchschnitt besser geworden.“ Die Opposition erwidert, dass kein Schüler durch die verschärften Aufnahmeprüfungen gefördert würde. Mehr Menschen würden von der höheren Bildung ausgeschlossen, zum Nachteil der Wettbewerbsfähigkeit des Landes.

Diese zugespitzten Formulierungen treffen den Kern nahezu jeder Diskussion zur Schulpolitik. Beispielsweise brüstet sich Bayern mit den herausragenden Leistungen seiner Abiturienten. Gleichzeitig hat Bayern aber auch die niedrigste Abiturientenquote aller Bundesländer. Dieser Je-schlechter-desto-besser-Effekt ist auch als Will-Rogers-Phänomen bekannt (Beck-Bornholdt/Dubben, 2001): Nehmen wir einmal die durchschnittlichen Leistungen der Schüler einer Klasse als Evaluationsmaßstab. Es möge zwei Parallelklassen geben, die in der Evaluation unterschiedlich gut abschneiden. Der Schulleiter sucht nun einen unterdurchschnittlichen Schüler der besseren Klasse aus, dessen Leistungen aber immer noch über dem Durchschnitt der anderen Klasse liegen. Der Wechsel dieses Schülers von der besseren zur schlechteren Klasse führt zu einer Verbesserung des Durchschnitts in beiden Klassen.

Klein-Gunter und die Zahnpasta. Klein-Gunters Mutter rügt: „Du putzt deine Zähne nicht, die Zahnpasta wird nicht alle.“ Zur Pflichterfüllung nach diesem Maßstab sollte es reichen, wöchentlich eine gehörige Portion Zahnpasta im Komposthaufen unterzuwühlen. Mit dieser Geschichte beginnt Gunter Dueck (2003) einen Artikel über Sinn und Unsinn der

Leistungsindikatoren und Evaluationsmaßstäbe. Gerade flattert mir wieder ein Hochschulkränkung auf den Tisch. (Natürlich muss es „ranking“ statt „kränkung“ heißen. Dieser „Freudsche Verschreiber“ ist mir wirklich passiert.) Diesmal ist die mittlere Studiendauer der Maßstab für das Ranking. Endlich mal was Objektives, denke ich. Aber da kommen mir Zweifel: Ich kenne Leute, die neben dem Studium Kinder großgezogen und solche, die noch vor dem Ende ihres Studiums eine Firma gegründet haben. Das ist ohne Studienzeitverlängerung nicht zu machen. Diese Leistungsträger unserer Gesellschaft schlagen negativ zu Buche.

Konsumforschung. Am 1. September 1999 liest man in der Fuldaer Zeitung einen Bericht über ein Konsum­for­schungsgutachten: „Interessant ... ist ..., dass über die Hälfte der Passanten täglich oder mehrmals pro Woche Fuldas Innenstadt aufsuchen. 25,8 Prozent kommen einmal pro Woche oder mindestens 14-täglich. Demnach kann davon ausgegangen werden, dass die Innenstadt ein umfangreiches Angebot für die Kunden bereithält.“ Offenbar ist beabsichtigt, die Tatsache, dass immerhin 50 Prozent der ange­trof­fe­nen Passanten täglich, und nur 25 Prozent wöchentlich kommen, als Zeichen der Attraktivität Ful­das hinzustellen. Verzerrte oder vorsortierte Stichprobe (Sample with the built-in bias) nennt man so etwas (Krämer, 1991; Huff, 1954), denn befragt werden kann nur, wer da ist. Aber das ist noch nicht alles. Die Schlussfolgerung ist völlig aus der Luft gegriffen, wie eine Grenzbetrachtung zeigt: Hätten hundert Prozent der Leute angegeben, täglich zu kommen, wäre jedem klar: In Fulda trifft man nur Fuldaer. Die Stadt ist für Auswärtige völlig uninteressant.

Zum Schluss noch etwas aus meinem Fachgebiet:

Je unzuverlässiger ein System ist, desto zuverlässiger weiß man das. Mit den hochzuverlässigen Systemen der Sicherheitstechnik hat man – was Fehler angeht – gottlob nur spärliche Erfahrungen. Bei der heutigen Bürosoftware weiß man dagegen ziemlich genau, was man sich damit einhandelt.

(3. Dezember 2005)

Zurück zur Übersicht

Expertenwissen erschwert das Problemlösen

Wer Neues finden will, muss bereits möglichst viel zum Thema wissen, er sollte Fachmann auf dem Gebiet sein. Das schient nahe zu liegen. Die meisten Menschen werden es wohl unterschreiben. Aber ist es wirklich so?

Widerspruch. Im Laufe einer Studie zur Funktionsweise des ersten Computers, nämlich der rein mechanisch arbeitenden Z1 von Konrad Zuse, machte ich eine überraschende Beobachtung. Mir und auch einigen meiner Kollegen, sie sind Experten auf dem Gebiet der Informatik, fiel es erstaunlich schwer, die Arbeitsweise des mechanischen Addierwerks zu verstehen. Horst Zuse, ältester Sohn des Erfinders, meinte gar: „Die Funktionsweise der arithmetischen Einheit (Binäres Gleitkommarechenwerk) ist Konrad Zuses Geheimnis geblieben und er hat es 1995 mit ins Grab genommen.“ – Vielleicht doch nicht. Meine Vermutung ist, dass wir in Bahnen denken, die durch die moderne Informatik und ihre Didaktik vorgegeben sind. Dieses Expertenwissen macht uns blind für Lösungen, die abseits der eingetretenen Pfade liegen. Dieses Expertenwissen hatte Konrad Zuse nicht. Er interessierte sich noch nicht einmal für die Technik der damals bekannten und gebräuchlichen mechanischen Rechenmaschinen, wie er selbst bekannte. Er ging eigene Wege. Ich vermute, dass Zuse gerade dadurch, dass er sich gar nicht erst in die Gedankenwelt der damaligen Rechentechnik begab, indem er also eine vorzeitig Blickverengung vermied, frei und fähig war, revolutionär Neues zu erfinden. Natürlich nutzte er Vorwissen, beispielsweise das binäre Zahlensystem, dessen Vorzüge er durch Schriften von Gottfried Wilhelm Leibniz kennenlernte. Er nahm sich aber die Freiheit, sich beim Lernen auf Wissen und Methoden zu konzentrieren, die ihm bei seiner Arbeit weiterhalfen; sein Wissenserwerb war problemgeleitet. Der von ihm zu Beginn ins Auge gefasste Bau eines Computers mit Relais brachte ihn auf eine grafische Darstellungsweise, die er abstrakte Schaltgliedtechnik nannte. Diese abstrakte Schaltgliedtechnik ist bestechend elegant und sie erfasst die wesentlichen Eigenschaften der Schaltelemente, nämlich das potentialfreie Schalten durch galvanisch getrennte Stromkreise mittels Relais. In den heute gebräuchlichen Symbolen der Schaltgliedtechnik kommt die galvanische Trennung von Stromkreisen nicht mehr zum Ausdruck, weil die eingesetzten Schaltkreistechnologien eine solche Trennung nicht bieten. Das führt zur Blickverengung. Es ist kein Wunder, dass Zuses elegante Lösung für den Addierer mit einschrittigem Übertrag heutzutage aus dem Blickfeld gerät.

Analyse. Dass Experten mit Problemen ihres Faches manchmal mehr Schwierigkeiten haben als die nicht so Geschulten, lässt sich auf Effekte zurückführen, die ich unter der Überschrift Automatisierung des Denkens und Handelns einordne.

Ein einfaches Beispiel. Bekannten und Freunden legte ich den folgenden Text vor und bat sie zu zählen, wie oft der Buch­stabe F vorkommt. Versuchen Sie es doch selbst einmal.

FINISHED FILES ARE THE RE-
SULT OF YEARS OF SCIENTIF-
IC STUDY COMBINED WITH THE
EXPERIENCE OF YEARS

Sie haben im Text drei-, vier-, oder fünfmal den Buchstaben F gefunden? Sehen Sie noch einmal genauer hin: Der Buchstabe F kommt sechsmal vor. Wir übersehen bei der ersten Begegnung mit diesem Text vorzugsweise das F im Wörtchen OF. Dies ist ein Wort, das in der Sprache mit hoher Häufigkeit auftritt und deshalb als eine Einheit gelesen und nicht erst aus Buchstaben zusammengesetzt wird. Verblüfft war ich, als eine Bekannte sofort die richtige Zahl nannte. Des Rätsels Lösung: Sie konnte kein Englisch und ist den Text Buchstabe für Buchstabe durchgegangen.

(7. Juni 2012)

Zurück zur Übersicht

Ein Egoismus-Paradoxon

Wer behauptet, der Mensch zerstöre seine Lebensgrundlagen durch die egoistische Verfolgung seiner Interessen, wird allgemeine Zustimmung ernten. Dabei wäre eine genauere Analyse angebracht. Formulieren wir etwas genauer: „Wenn wir eine Population von wildlebenden Tieren - z. B. Großwale - maximal ausbeuten, gefährden wir deren Bestand.“ Auch dieser Satz wird wohl meist bejaht.

Widerspruch. So allgemein hingesagt stimmt der Satz nicht. Zur Widerlegung nehmen wir der Einfachheit halber an, die fragliche Population unterliege einem einfachen Gesetz des begrenzten Wachstums. Der anfangs kleine Bestand x möge jährlich um einen bestimmten Prozentsatz r - sagen wir r=5% - wachsen. Je größer die Population ist, umso mehr verringert sich diese Zuwachsrate, weil nicht genug Futter für den Nachwuchs da ist. Wir müssen also mit einer bestandsabhängigen Zuwachsrate rechnen. Diese Zuwachsrate geht gegen null, wenn sich die Größe x der Population einem Wert nähert, der von der Umwelt gerade noch verkraftet wird. Dieser Wert wird als Kapazität K bezeichnet. Wir setzen hier einmal K=100. Ein für unsere Zwecke brauchbarer Ansatz für die Zuwachsrate ist r(1-x/K). Die Multiplikation der Zuwachsrate mit dem Bestand ergibt bekanntlich die Wachstumsgeschwindigkeit der Population: r(1-x/K)x. Durch Jagd soll der Zuwachs „abgeerntet“ werden.

 

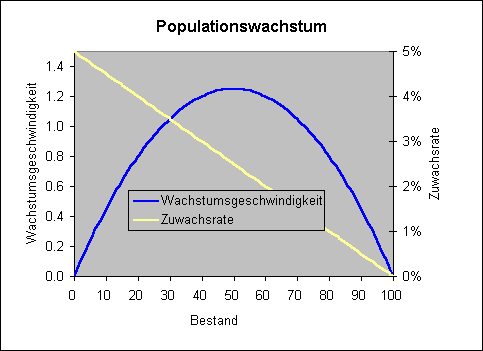
ChartObject Populationswachstum

 

Wer einen maximalen Ertrag anstrebt, wird die Population auf den Wert x = K/2 = 50 anwachsen lassen und sie dann durch Bejagen bei diesem Bestand halten. Das Streben nach maximalem Ertrag sichert demzufolge einen ausreichenden Bestand der bejagten Population - entgegen der zunächst geäußerten Meinung.

Kommentar. Wenn wir - ganz Egoisten - den langfristig haltbaren Höchstertrag anstreben, müssen wir nach dem Prinzip der Nachhaltigkeit (Sustainability) wirtschaften. Das nützt uns und der Umwelt. Dass wir das oft nicht tun, liegt daran, dass viele Jäger um die Beute konkurrieren und dass jeder einen möglichst großen Teil des „Kuchens“ abkriegen will. Es ist unsere Unfähigkeit, die so genannte Tragödie der Gemeingüter (Tragedy of the Commons) zu verhindern, die uns in Schwierigkeiten bringt. Der eng- und kurzsichtige Egoist macht sich und anderen Probleme - nicht dagegen der „Weitwinkelegoist“. (Siehe auch das Literaturverzeichnis meines Kurses über Umweltsimulation: Wilson/Bossert, Odum und Global 2000.)

 (31.8.1999)

Zurück zur Übersicht

Das Paradoxon der Restlebensdauer

Wir befinden uns an einem Highway im mittleren Westen der USA. Die Gegend ist entlegen, nur wenige Häuser und eine Tankstelle stehen am Highway. Die nächste Ortschaft ist weit weg. Ab und zu kommt ein Auto vorbei. Im Laufe eines Nachmittags, also innerhalb von 6 Stunden sind es etwa 36 Wagen. Sie kommen rein zufällig. (Der Mathematiker spricht von einem Poissonstrom mit einer Intensität von 6 Wagen je Stunde.) Irgendwann am Nachmittag tritt ein Anhalter an die Straße und wartet auf das nächste Auto, das ihn wohl zum nächsten Ort mitnehmen würde. Wie lange wird der Anhalter im Mittel warten müssen, bis der nächste Wagen kommt?

Unten ist einmal die Situation über der Zeit aufgetragen: Jedes vorbeikommende Auto wird auf der Zeitachse mit einem „o“ markiert. Der Zeitpunkt, zu dem der Anhalter auftritt, erhält das „x“. Die Wartezeit des Anhalters ist w. Gesucht ist offenbar der Erwartungswert von w.

├─────o───o───x─────────o────────────o─o───────> Zeit

├────────────┼──── w ───┤

Widerspruch. Schnell gefunden – und falsch – ist diese Antwort: Der Anhalter muss im Mittel 5 Minuten warten. „Begründung“: Der mittlere zeitliche Abstand zwischen den Wagen beträgt 10 Minuten. In ein solches typisches Intervall fällt rein zufällig die Ankunft des Anhalters. Das kann genauso wahrscheinlich am Anfang oder am Ende des Intervalls oder auch sonst wo im Intervall sein. Wenn man über alle möglichen Fälle den Mittelwert nimmt, kommt man auf die 5 Minuten. Ist doch klar. Oder? Ein Einwand könnte folgendermaßen lauten: Es ist ähnlich wie beim Lottospiel. Nur weil ich schon lange keinen Gewinn hatte, rückt ein möglicher Gewinn nicht näher. Also: Egal wie lange es schon her ist, dass das letzte Fahrzeug vorüber gefahren ist, die Zeit bis zum nächsten Eintreffen eines Fahrzeugs wird dadurch nicht beeinflusst. Die Zeit bis zum nächsten Fahrzeug unterliegt derselben Statistik wie die Zeit zwischen zwei Fahrzeugen. Also muss der Anhalter im Mittel 10 Minuten warten.

Analyse. Zu logischen Schnellschüssen und Fehlschlüssen kommt es durch die übertriebene Reduktion von Merkmalen einer Situation, durch Blickverengung also. Eine Folge des Scheinwerferprinzips und der Prägnanztendenz.

Ein einfacheres Problem, dessen Lösung auch den Kern des Paradoxons der Restlebensdauer trifft, ist das folgende: Werktags komme ich immer so zwischen vier und fünf Uhr nachmittags an den Stachus und will mit der U-Bahn zum Hauptbahnhof fahren. Obwohl die Züge in beide Richtungen etwa gleich dicht fahren, kommt in 9 von 10 Fällen zuerst ein Zug, der in Richtung Ostbahnhof fährt. Ist das Pech oder liegt es am Fahrplan? Eine ähnliche Situation wird im Preisrätsel „Zufallsbekanntschaften“ im Spektrum der Wissenschaft vom Mai 2000 dargestellt. Die Auflösung steht im Juli-Heft.

Eine ausführliche und gründliche Analyse des Paradoxons der Restlebensdauer ist im Rahmen der Erneuerungstheorie möglich (Kleinrock, Band I, 1975, S. 169 ff.). Eine kurze und elementare Darstellung der Zusammenhänge enthalten meine Anmerkungen zur Erneuerungstheorie (ca. 80 KB).

(23.8.2000)

Zurück zur Übersicht

Eine Programmierstudie

Aufgabenstellung. Angenommen, die „<„-Relation des Computers funktioniert nicht. Die Funktion

LESS(a, b: REAL): BOOLEAN

soll genau dann den Wert TRUE liefern, wenn a<b ist. Wie lässt sich das realisieren?

Die Antworten von 19 Befragten:

  • fünfmal: IF b-a>0 THEN less:= TRUE ELSE less:= FALSE
  • zweimal: IF (a>b) OR (a=b) THEN less:= FALSE ELSE less:= TRUE
  • viermal: IF b>a THEN less:= TRUE ELSE less:= FALSE
  • dreimal: IF NOT(a>=b) THEN less:= TRUE ELSE less:= FALSE
  • zweimal: less:= NOT(a>=b)
  • einmal: less:= b>a
  • zweimal: IF a>=b THEN less:= FALSE ELSE less:= TRUE

Analyse

  • Alle Lösungen sind korrekt.
  • Die einfachste Lösung ist am schwersten zu finden: less:= b>a.
  • Boolesche Ausdrücke scheinen „funktional“ an Entscheidungen „gebunden“ zu sein, was nicht stimmt. Ein Einstellungseffekt.
  • Die Reihenfolge der Variablen scheint unabänderlich zu sein, was nicht stimmt. Eine Folge der Strukturerwartung.

(1998)

Zurück zur Übersicht

Die rutschende Leiter

Aufgabe. Eine Leiter steht zunächst senkrecht an der Wand. Dann wird ihr Fußende langsam von der Wand weggezogen, bis die Leiter ganz auf dem Boden liegt. Auf welcher Kurve bewegt sich dabei der Mittelpunkt der Leiter? Ist die Kurve konkav oder konvex - also nach unten oder nach oben gekrümmt?

Widerspruch. Intuitiv wird meist eine konvexe, tangential an Wand und Boden anliegende Kurve vermutet. Tatsächlich aber bewegt sich der Mittelpunkt der Leiter, die an der Wand herabrutscht, genau so wie der Mittelpunkt einer Leiter, die einfach kippt, bei der also der Fußpunkt unverändert an der Wand bleibt. Dass das so ist, ergibt sich aus folgendem Gedankenexperiment: Man stelle sich die beiden Leitern in der Mitte verbunden vor, wie eine Schere. Beim Öffnen dieser „Schere“ rutscht die eine Leiter an der Wand entlang und die andere kippt. Der gemeinsame Mittelpunkt bewegt sich also auf einem Viertelkreis, dessen Enden auf Wand und Boden senkrecht stehen; er beschreibt eine konkave Kurve.

Analyse. Wie kommt es zu der ursprünglichen intuitiven und falschen Antwort? Man kann sich den Irrtum so erklären: Wir stellen uns vor, wie die Leiter fällt. Dazu bilden wir im Kopf Modelle der Gegenstände und bewegen sie probeweise.  Dieses Probehandeln im vorgestellten Raum ist eine Art „Simulation im Kopf“. Albert Einstein sieht darin – wie vormals bereits Sigmund Freud – das Wesen des Denkens: „Die geistigen Einheiten, die als Elemente meines Denkens dienen, sind bestimmte Zeichen und mehr oder weniger klare Vorstellungsbilder, die 'willkürlich' reproduziert und miteinander kombiniert werden können ... dieses kombinatorische Spiel scheint die Quintessenz des produktiven Denkens zu sein“ (Krech/Crutchfield, 1992).

Der Irrtum liegt aber nicht im Probehandeln selbst, sondern in der fehlgeleiteten Beobachtung und Auswertung: Aufgrund der Prägnanztendenz, also der Übertreibung wesentlicher Merkmale, treten auffällige Charakteristika in den Vordergrund. Andere Phänomene können durch das prägnantere in den Hintergrund gedrängt werden. So ist es im Falle der rutschenden Leiter. Die Hüllkurve (Einhüllende, Enveloppe) der Leiterbewegung drängt sich in den Vordergrund. Die Bewegung des Mittelpunkts der Leiter ist dagegen in der Vorstellung nur schwer zu verfolgen. Die folgenden Grafiken machen das deutlich.

 

 

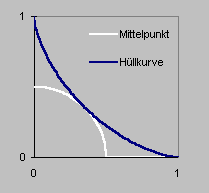
Die Prägnanztendenz ist normalerweise ein äußerst nützlicher Mechanismus. Meist liegen wir damit richtig. (Sonst wäre der Mechanismus mangels Fitness seiner Anwender bereits ausgestorben.) Aber in außergewöhnlichen Situationen kann es auch zu Fehlern kommen – wie hier geschehen. Es liegt eine Denkfalle vor, eine kognitive Täuschung also.

(31.8.1999)

Zurück zur Übersicht

Das Drei-Türen-Problem

Das Drei-Türen-Problem – auch Ziegenproblem genannt (Der Spiegel, 34/1991, S. 212-213). Große Fernsehshow. Der Supergewinn verbirgt sich hinter einer von drei Türen. Der Kandidat trifft seine Wahl. Die Tür wird jedoch zunächst nicht geöffnet. Der Showmaster öffnet eine der beiden anderen Türen, wohl wissend, dass dahinter eine Ziege als lebende Niete angepflockt ist. Der Showmaster stellt dem Kandidaten nun frei, bei seiner ursprünglichen Wahl zu bleiben, oder die dritte der Türen zu öffnen. Soll er, oder soll er nicht?

Widerspruch. Der Alltagsverstand entscheidet meist, dass es sich nicht lohnt, neu zu wählen. Bestenfalls kommt man zum Schluss, dass es egal ist, was man macht (Fifty-fifty-Irrtum). Diese Fehlurteile wurden selbst von renommierten Wissenschaftlern und Statistikern abgegeben (Stewart, 1991). Aber es verhält sich ganz anders. Mit etwas Wahrscheinlichkeitsrechnung lässt sich Klarheit gewinnen: Hinter der vom Kandidaten gewählten Tür steckt der Hauptgewinn mit der Wahrscheinlichkeit 1/3. Mit der Wahrscheinlichkeit 2/3 steckt der Hauptgewinn hinter einer der beiden anderen Türen. An diesen Wahrscheinlichkeiten ändert sich durch die Offenbarung einer Niete durch den - voraussetzungsgemäß gut informierten - Showmaster gar nichts. Der Showmaster liefert Information. Und diese kann der Kandidat nutzen. Wenn er auf die andere noch nicht geöffnete Tür wechselt, verdoppelt er seine Gewinnchance auf 2/3.

Analyse. Der populäre Fifty-fifty-Irrtum beruht vermutlich auf einer sorglosen Anwendung des Indifferenzprinzips („Wenn keine Gründe dafür bekannt sind, um eines von verschiedenen möglichen Ereignissen zu begünstigen, dann sind die Ereignisse als gleich wahrscheinlich anzusehen“, John Maynard Keynes). Anstatt es auf die Ausgangssituation anzuwenden, wird das Prinzip auch auf die durch den Showmaster veränderte Situation angewandt. Der Fehler geht wohl auf die Automatisierung des Denkens und Handelns zurück, es handelt sich um einen Einstellungseffekt.

Nachträge (17.12.03, 4.12.05). Seit ich das Drei-Türen-Problem in diese Sammlung aufgenommen habe, erreichen mich immer wieder Zuschriften. Die Absender wollen mich davon überzeugen, dass die Chancen, hinter einer der zwei noch geschlossenen Türen den Hauptgewinn zu finden, fifty-fifty sind. Ihnen rate ich zu einem Spiel unter Freunden und Verwandten: Drei umgedrehte Kaffeetassen  ersetzen die Türen. Ein Spielleiter versteckt als Hauptgewinn eine Münze unter einer der Tassen. Und dann geht es weiter nach den Regeln der Fernsehshow. Wenn das etwa zwanzigmal durchexerziert wird, fällt auch der Hartnäckigste von seinem „Gleichverteilungsglauben“ ab. Ausführlich wird das Drei-Türen-Problem von Gero von Randow (2004) behandelt.

Variante mit vergesslichem Showmaster. Auf folgende Komplikation hat mich Peter Seizer, Neu Ulm, aufmerksam gemacht: Was ist, wenn der Showmaster selbst nicht mehr weiß, hinter welcher Tür der Gewinn steckt. Er stößt nur rein zufällig auf die Niete. Was sagt uns die Wahrscheinlichkeitsrechnung jetzt? Die Wahrscheinlichkeit, dass der Kandidat ursprünglich richtig gewählt hat, ist nach wie vor 1/3. Der Quizmaster kann in diesem Fall nichts falsch machen. Hat der Kandidat ursprünglich falsch gewählt - das passiert in zwei von drei Fällen - so wird der Showmaster mit 50-prozentiger Wahrscheinlichkeit die Show schmeißen, weil er versehentlich die Tür mit dem Hauptgewinn öffnet. Er beraubt also den Kandidaten der Hälfte seiner Chancen, bei einem Wechsel selbst den Hauptgewinn zu ziehen. Egal was der Kandidat macht, seine Chancen stehen jetzt tatsächlich fifty-fifty.

Variante mit den drei Todeskandidaten. Drei Gefangene wissen, dass zwei von ihnen hingerichtet werden sollen. Was sie nicht wissen ist, wer von ihnen überleben wird. Einer von ihnen stellt folgende Überlegung an: „Ich habe eine Chance von 1/3, nicht hingerichtet zu werden. Ich kann meine Chance verbessern, wenn ich den Gefängniswärter dazu bringen kann, mir den Namen eines meiner Mitgefangenen zu nennen, der hingerichtet wird. Dann bleiben nämlich nur noch zwei Möglichkeiten: Entweder bin ich der andere, oder nicht. Meine Überlebenschance ist dann 50 %“ (Székely, 1990, S. 73). Das ist natürlich ein Fehlschluss, ähnlich dem beim Drei-Türen-Problem. (Allenfalls der Dritte im Unglücksbunde hätte Grund zu verhaltener Freude.)

(15. Januar 00)

Zurück zur Übersicht

Mentale Landkarten

Wenn ich frage, ob London weiter östlich oder weiter westlich, weiter nördlich oder weiter südlich als Berlin liegt, bekomme ich meist die Antwort: London liegt nordwestlich von Berlin.

Widerspruch. London liegt aber weiter südlich als Berlin. Das zeigt ein Blick auf die Landkarte. Woher kommt der Irrtum bezüglich der Nord-Süd-Richtung?

Analyse. Bei der „mentalen Grenzziehung“ kommt es aufgrund der Prägnanztendenz zu Begradigungen und Vergröberungen. An diesen prägnanten Grenzen orientieren wir uns. Folglich werden Orte in Gedanken systematisch verrückt (Anderson, 1988, S. 94). Im Fall London-Berlin erkläre ich mir die zu beobachtende Verzerrung so: Bezogen auf die Nordsee liegt England im Westen und Deutschland im Süden. Der Ärmelkanal wird auf seine Ost-West-Richtung hin „begradigt“. Durch diese Vereinfachung „rutscht“ England gedanklich gen Norden.

(22. August 01)

Zurück zur Übersicht

Die Parallelogramm-Aufgabe

Ein Parallelogramm ist durch zwei Geraden, die von einer Ecke ausgehen, in drei flächengleiche Stücke zu teilen - etwa so (Dörner, 1979):

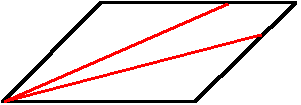
Zugelassen sind für die Konstruktion nur die in der Geometrie üblichen Hilfsmittel: Zirkel und Lineal.

Schritt für Schritt zur Lösung. Die meisten Menschen sehen die Lösung nicht auf Anhieb. Schlimmer noch: Auch längeres Grübeln hilft nicht weiter. Man dreht sich im Kreise. Sie auch? Dann gebe ich einen Tip: Lassen Sie doch einmal eine der Bedingungen („... von einer Ecke ausgehen ...“, „... flächengleich ...“) weg. Vielleicht hilft das auf die Sprünge. Ich habe es mit Studenten und Freunden ausprobiert: Die allgemein gehaltenen Anregungen können helfen, die eingefahrenen Denkpfade zu verlassen. Das ist die Methode, die Georg Pólya in seiner berühmten „Schule des Denkens“ (1949) propagiert. Es ergibt sich in den meisten Fällen ein typischer Denkablauf. Mehr über das Problemlösen finden Sie in meiner Lektion  Schöpferisches Denken - Heuristik.

(20. April 00)

Zurück zur Übersicht

Pascals Wette auf die Existenz Gottes - Pascal’s wager

Der französische Religionsphilosoph, Mathematiker und Physiker Blaise Pascal (1623-1662) suchte eine rationale Verteidigung seines Glaubens. Von ihm stammt die folgende Wette: Wenn du an Gott glaubst - sozusagen auf ihn setzt - und Gott existiert nicht, so verlierst du nichts. Wenn du aber nicht an Gott glaubst und Gott existiert, dann kommst du in die Hölle. Deswegen ist es vernünftig, an Gott zu glauben. So wahrst du deine Chance, in den Himmel zu kommen.

Widerspruch. Was ist, wenn Gott alle diejenigen gar nicht mag, die aus reinen Vernunftgründen an ihn glauben? Das liegt sogar nahe; denn schon der Verstoß gegen das Verbot, vom „Baum der Erkenntnis des Guten und Bösen“ zu essen hatte ja drastische Folgen (1. Mose 2, 17). Was ist, wenn Gott das Universum dem Teufel überlassen hat? Oder wenn es in der Hölle recht lustig, im Himmel dagegen ziemlich langweilig ist? Oder wenn ... Lässt man der Phantasie freien Lauf, verflüchtigt sich die scheinbar zwingende Kraft des Pascalschen Arguments für den Glauben.

Analyse. Rationalismus und Aufklärung waren äußerst erfolgreiche Denkrichtungen in unserer Ideengeschichte; kein Wunder also, dass die Rationalität des Menschen hoch eingeschätzt und auch überschätzt wurde. Viel war mit Vernunft erklärbar, warum nicht auch Gott? Aber Logik und Gedankenschärfe allein ermöglichen keine Erklärung der Natur oder gar des Übernatürlichen. Es müssen Vermutungen, Vorurteile, Hypothesen, Theorien hinzukommen, also das prinzipiell Unbeweisbare, das nur an praktischen Resultaten Prüfbare. An den Überprüfungsmöglichkeiten hapert es bei der Religion. Deshalb muss die durchaus erlaubte Methode der Einengung des gedanklichen Spielraums hier daneben gehen. Es gibt keine Denknotwendigkeit, den Scheinwerfer der Erkenntnis auf ein Bild von Himmel und Hölle zu richten, wie es Bibel (Matthäus 25, 31) und Eschatologie ausmalen. Es fehlt der Erfahrungshintergrund, der eine solche Einengung der Menge aller prinzipiell denkbaren Welten auch nur nahe legen oder in irgendeiner Weise stützen könnte. Unser Hang zur Bildung von einschränkenden Hypothesen ist es, der Wissenschaft überhaupt erst möglich macht. Dieser Hang ist es aber auch, der uns anfällig macht für die Manipulation unserer Gedanken durch andere. Wir durchschauen meist nicht sofort, dass eine Hypothese - wie die der Existenz von Himmel und Hölle - leer und nutzlos ist. Wir übersehen allzu leicht, dass es widerlegende Erfahrungen gar nicht geben kann. Und eine Hypothese über die Beschaffenheit der Welt, die prinzipiell nicht an der Erfahrung scheitern kann, beinhaltet keinerlei Erkenntnis über diese Welt. Sinnvolle und begründete Prognosen lassen sich damit nicht gewinnen. Die Möglichkeit einer rationalen Entscheidung wird bei der Pascalschen Wette also nur vorgetäuscht.

Links und Lesehinweise. Die Pascalsche Wette habe ich auf der Web-Seite von Volker Dittmar gefunden. Eine ziemlich ausführliche Darstellung des Für und Wider aus dem Blickwinkel der Entscheidungstheorie und viele Literaturhinweise bietet die Stanford Encyclopedia of Philosophy. Wer Originalbeiträge von Gläubigen, Agnostikern und Atheisten sucht, möge das Stichwort „Pascal’s Wager“ in eine Suchmaschine eingeben. Mit Google kommt man zurzeit auf über 10000 (zehntausend!) Treffer. Wie Bilder von Himmel und Hölle entstehen und welche Funktion sie haben, zeigt der Wissenschaftspublizist Martin Urban (2002) unter Zugabe einer gehörigen Portion Skepsis. Eine Einführung in das skeptische Denken bietet Christoph Bördlein (2002) an.

(22. September 2003)

Zurück zur Übersicht

Lügnerparadoxon (The liar paradox)

Der Satz „Ich lüge“ ist die Kurzversion des Lügnerparadoxons. Der Satz lässt wenigstens die folgenden drei Auffassungen zu:

1.      Ich lüge immer

2.      Ich lüge manchmal

3.      Ich lüge gerade

Die ersten beiden Auffassungen bieten keine Schwierigkeiten: Der Sprecher ist ein ganz normaler Mensch, der halt hin und wieder lügt, meistens aber die Wahrheit spricht. Im 1. Fall lügt er gerade und im 2. nicht.

Widerspruch. Interessant ist der 3. Fall. Hier taucht die Schwierigkeit in dem Moment auf, in dem man den Satz mit der Glaubwürdigkeit des Sprechers verknüpft: Gilt der Satz, lügt der Sprecher und der Satz muss falsch sein. Gilt er nicht, sagt der Sprecher die Wahrheit; und das kann ja nun ebenfalls nicht stimmen. Das klingt tatsächlich paradox.

Analyse. Die Aussagevariablen A möge für die Aussage „Ich lüge“ stehen. Der Kern der Angelegenheit kommt zu Tage, wenn man die ausgesprochene Aussage mit der Aussage über ihren Wahrheitswert kombiniert: Meine Aussage (A) ist genau dann wahr, wenn ich gerade nicht lüge (¬A). Formal liefert das den kombinierten Ausdruck A = ¬A. Diese Aussage ist äquivalent zu A¬A. Sie ist logisch falsch. Es gibt keine Möglichkeit, der Variablen A einen logischen Wert (wahr oder falsch) zuzumessen derart, dass die kombinierte Aussage wahr wird.

Eine logisch falsche Aussage ist noch immer eine logische Aussage. Nur existiert eben die Welt nicht, in der sie gilt. Der Logiker sagt es so: Die Erfüllungsmenge der Aussage ist leer. Deshalb spreche ich lieber von einer unerfüllbaren Aussage und nicht von einem Paradoxon. An unerfüllbaren Aussagen ist überhaupt nichts dran, was zu endlosem Grübeln verführen müsste. Jeder darf einmal Unsinn reden, und der Satz „Ich lüge“ in der 3. Auffassung ist eben Unsinn, nichts weiter. (Wir versuchen ja auch nicht, Äußerungen wie „Shubidubidu“ oder „Hol’s der Teufel“ als wahr oder falsch einzustufen.)

Das Lügnerparadoxon ist ein typischer Selbstbezug. Ein Selbstbezug besteht aus einer Aussage, die – auf der Metaebene – gleichzeitig etwas über diese Aussage aussagt. Ein berühmter Selbstbezug steht in der Bibel, und zwar in einem Brief des Paulus an Titus 1, 12: „Es hat einer von ihnen ge­sagt, ihr eigener Prophet: Die Kreter sind immer Lügner, böse Tiere und fau­le Bäuche.“

Eine unerfüllbare Aussage entsteht erst dann, wenn die Aussagen auf der Kommunikationsebene und die auf der Metaebene einander widersprechen. Solche Aussagen werden von Watzlawick, Beavin und Jackson (1969) auch semantische Antinomien oder semantische Paradoxien genannt.

Das Lügnerparadoxon ist eine semantische Antinomie, der Selbstbezug des Paulus dagegen nicht: Die gemachte Aussage ist verträglich mit der Situation, dass der Prophet gerade lügt und es wenigstens einen Kreter gibt, der nicht durchweg lügt oder der kein fauler Bauch ist. Eine weitere Möglichkeit ist, dass Paulus einfach falsch berichtet hat. Seine  Bekräftigung („Dies Zeugnis ist wahr“) macht die Sache nicht besser.

Der Selbstbezug „Ich lüge nicht“ ist ohne inneren Widerspruch. Aussage und Metaaussage  verbinden sich hier zu einer Aussage vom Typ A=A. Sie ist logisch - also unter allen Umständen - wahr. Und sie besagt nichts, auch nichts darüber, ob ich nun lüge oder nicht. (Natürlich lüge ich nicht. Aber Sie können das nicht wissen!)

(06.09.2004, korr.: 29.12.06, 12.06.09)

Zurück zur Übersicht

Henkerparadoxon (The unexpected hanging)

Am Samstag wird folgendes Urteil ge­spro­chen: „Die Hin­richtung wird mittags an einem der sieben Tage der nächsten Wo­che statt­fin­den. Aber Sie werden nicht wissen, an welchem Tage, bis Sie am Mor­gen des Hin­­richtungstages Bescheid be­kom­men.“

Widerspruch. Nun, wenn bis Freitag nichts passiert ist, schließt der Todeskandidat, kann auch am Samstag der Henker nicht mehr kom­men, denn er käme dann ja nicht un­ver­hofft. Also ist der Samstag aus­ge­schlos­sen. Wie aber steht's dann mit Frei­tag? Auch der Freitag ist mit demselben Ar­gument ausgeschlossen. So weiterfahrend kommt der Kandidat zum Schluss, dass der Henker eigentlich an keinem Tag der Woche kommen kann. Am Mittwochmorgen aber trifft ihn die entsetzliche Nach­richt – unverhofft!

Verschärfung des Widerspruchs. Da der Todeskandidat bewiesen hat, dass er nicht hingerichtet werden kann, würde ihn die Nachricht selbst am Samstag noch überraschen. Das Urteil ist im Nachhinein gesehen (scheinbar) wahr, gerade weil es für falsch gehalten wird.

Analyse. Viel ist schon über dieses Paradoxon geschrieben worden. Als Beispiel nenne ich Poundstone (1988, S. 110 ff.). Früher habe ich mich mit einem Erklärungsversuch abgefunden, der darauf hinausläuft, dass die Anwendbarkeit der Logik eben ihre Grenzen hat und dass sie uns über diese Grenzen leider nicht informiert. Heute denke ich, dass die Sache viel einfacher liegt:

1.      Die Logik ist anwendbar und

2.      bei richtiger Anwendung der Logik verschwindet das Paradoxon.

So wie der Todeskandidat das Urteil interpretiert, läuft es auf eine logisch falsche Aussage hinaus, wie etwa der Satz „Heute regnet es und heute regnet es nicht“. Warum?

Offenbar entstehen die Schwierigkeiten durch die Lesart des Urteils durch den Todeskandidaten: „Die Hin­richtung wird mittags an einem der sieben Tage der nächsten Wo­che statt­fin­den. Und gleichgültig, an welchem Tag das ist, Sie werden nicht wissen wann, bis Sie am Mor­gen des Hin­­richtungstages Bescheid be­kom­men.“ In dieser Interpretation ist die Aussage unter allen Umständen falsch. Denn aus ihr lässt sich schlussfolgern, dass auch am Samstag eine überraschende Hinrichtung möglich ist. Und das ist gleichzeitig unmöglich. Das so verstandene Urteil wird auch im Nachhinein nicht wahr, egal was passiert.

Aus einer widersprüchlichen – einer logisch falschen und unerfüllbaren Aussage also – lassen sich grundsätzlich keine gültigen Schlüsse ziehen. Genau genommen lassen sich aus einer logisch falschen Aussage beliebige Aussagen herleiten – wahre und falsche. Aber das hilft nicht weiter. In diesem Sinne fehlt der Argumentation des Todeskandidaten das Fundament.

Die Widersprüchlichkeit des Urteils wird durch das Einbeziehen mehrerer Tage wirkungsvoll verhüllt. Und genau das ist die Denkfalle: Wegen der Sinnsuche unseres Wahrnehmungsapparats und der daraus folgenden Überschätzung des Ordnungsgehalts der Dinge stellen wir halbwegs plausible Aussagen nicht in Frage.

Anders als beim Lügnerparadoxon müssen wir die Aussage des Richters hier nicht einmal als Unsinn qualifizieren, dem jeder Wahrheits- oder Falschheitsgehalt abgeht: Die Aussage ist – so wie der Todeskandidat sie auffasst – einfach logisch falsch.

Der Richter hätte den Selbstwiderspruch durch eine kleine Ergänzung des Urteils ausschließen können: „… es sei denn, die Hinrichtung findet am nächsten Samstag, am siebenten Tag also, statt.“ Für den Todeskandidaten hätte das faktisch nichts geändert. Nur falsche Hoffnungen hätte er sich dann nicht mehr machen können.

 (13.12.2003, korr.: 27.12.06, präzisiert aufgrund eines Briefwechsels mit Günter Feuer: 01.04.07)

Zurück zur Übersicht

Keine Regel ohne Ausnahme

Dieses Beispiel findet der Leser – zumindest dem Sinn nach und etwas  ausführlicher – in den Kommentaren zu meinem Hoppla!-Artikel „GWUP: Esoterik durch die Hintertür“. Dort wird ein bekannter Philosoph folgendermaßen zitiert:

 

Natürlich ist der Satz „was ich jetzt sage, ist falsch“ antinomisch. Denn ist er wahr, so ist er falsch, und ist er falsch, so ist er wahr. Aber schon die Regel „keine Regel ohne Ausnahme“ ist nicht antinomisch, sondern nur falsch. Nimmt man sie nämlich als wahr an, so ist sie — wie gezeigt wurde — falsch; aus der Annahme, sie sei falsch, folgt dagegen nicht, dass sie wahr wäre. Sie ist demnach falsch. Von einer Antinomie kann keine Rede sein.“

 

Widerspuch. Die Aussage „Keine Regel ohne Ausnahme“ ist entweder wahr oder falsch. Jedenfalls gibt es keine Subjektvariable, von der der Wahrheitswert der Aussage abhängen könnte, denn die Subjektvariable „Regel“ ist an den negierten Existenzquantor „Keine“ gebunden und für konkretisierende Ersetzungen folglich nicht mehr frei. So interpretiert, kann die Aussage „Keine Regel ohne Ausnahme“ gar keine Regel sein, sondern bestenfalls eine Definition dessen, was wir unter einer Regel verstehen wollen. Dann ist die Aussage notgedrungen wahr. Eine Selbstanwendung ist ausgeschlossen. Eine Selbstanwendung setzt der zitierte Philosoph aber stillschweigend voraus. Daraus kann nichts werden.

 

Analyse. Mehr Bewegung kommt in die Sache, wenn wir den Satz sinnerhaltend umformulieren: „Wenn etwas eine Regel ist, dann gibt es dazu wenigstens eine Ausnahme.“ Anstelle von etwas kann jetzt jede mögliche Regel stehen. Jetzt haben wir ein Prädikat, das auf alle möglichen Regeln und darüber hinaus anwendbar ist und man kann es tatsächlich als eine Regel auffassen. Ich nenne sie hier die sonderbare Regel. Der Selbstanwendung der sonderbaren Regel steht jetzt nichts mehr im Wege. Die zentrale Frage ist nun, ob die sonderbare Regel auf sich selbst angewendet wahr oder falsch ist.

 

Die Menge der Regeln lässt sich aufteilen in eine Teilmenge A der Regeln mit und in eine dazu komplementäre Teilmenge B der Regeln ohne Ausnahmen. Dabei bleibt die sonderbare Regel zunächst unberücksichtigt. Zwei Fälle sind zu unterscheiden:

 

Fall 1: B ist nicht leer; es gibt Regeln ohne Ausnahmen.
Fall 2: B ist leer; Regeln ohne Ausnahmen gibt es nicht.

 

Fall 1 bietet keinerlei Probleme. Die sonderbare Regel hat Ausnahmen, nämlich wenigstens die der Menge B. Wir können die sonderbare Regel widerspruchfrei der Menge A zuordnen. Im Fall 2 kommt es zur Antinomie. Ordnen wir nämlich unsere sonderbare Regel der Menge A zu, dann bleibt die Menge B leer und es gibt nach wie vor keine Regeln ohne Ausnahmen. Damit ist die sonderbare Regel für sämtliche Regeln wahr. Das aber heißt: sie gilt ausnahmslos. Folglich gehört sie nicht zu A, sondern zu B. Nun ist die Menge B nicht mehr leer. Also auch die sonderbare Regel hat eine Ausnahme. Und genau diese Tatsache zwingt sie wieder zurück in die Menge A, wodurch sich die  Menge B wieder leert. Das ist das für eine Antinomie typische Hin-und-her.

 

(22.07.2015)

Zurück zur Übersicht

Mustererkennung ohne Muster

Gegeben sind zwei Bitfolgen der Länge zehn. Die erste Bitfolge ist 1001010110, und die zweite ist 0100000001. Wir fragen danach, welche der Folgen am ehesten durch reinen Zufall – beispielsweise durch das wiederholte Werfen einer fairen Münze – entstanden sein könnte. Die erste Bitfolge scheint zufällig zu sein. Die zweite Folge sieht verdächtig aus: Sie enthält sieben Nullen in Folge, ein ganz besonderes Muster also. Im Falle des Glücksspiels würde man von einer Pechsträhne reden (oder von einer Glückssträhne – je nachdem).

 

Widerspruch. Tatsächlich ist die zweite Folge rein zufällig entstanden, die erste nicht. Die Wahrscheinlichkeit, dass es in eine reinen Zufallsfolge aus zehn Bits zu einem Abschnitt aus sieben gleichen Werten (Nullen oder Einsen) kommt, ist gar  nicht so klein. Sie beträgt 4 % (Querbeet-Aufgabe Nr. 24). Auch bei der ersten Folge spielt der Zufall eine Rolle. Aber beim näheren Hinsehen stellt sich heraus, dass die Folge aus fünf Paaren aus zueinander komplementären Bits zusammengesetzt ist. (Freilich können derartig regelhafte Folgen auch rein zufällig entstehen. Sie haben eine Wahrscheinlichkeit von 3 %.)

 

Analyse. Moderne Wissenschaft und Aberglaube liegen nicht allzu weit auseinander. Sie nähren sich aus derselben Quelle, nämlich aus unserer Neugier und aus unserer Fähigkeit zu lernen. Die Grundmechanismen des Wissenserwerbs sind die Strukturerwartung, die Begabung zur Mustererkennung, die Kausalitätserwartung und die Befähigung zu Erweiterungsschlüssen, zur Induktion also. Diese angeborenen Lehrmeister machen wissenschaftliches Arbeiten überhaupt erst möglich. Aber sie haben eine okkulte Kehrseite: Wir sehen manchmal auch dort Muster, wo es eigentlich gar nichts zu sehen gibt. Beispielsweise können wir in Wolkenbildern Gesichter erkennen. In Rauchwolken auch. Berüchtigt ist das vermeintliche Teufelsgesicht in den Rauchwolken, die am 11.9.2001 aus dem World Trade Center schlugen (Inernet-Suchbegriffe: Devil’s Face WTC).

 

Im Film „A Beautiful Mind“ spielt Russell Crowe den berühmten Wirtschaftswissenschaftler und Spieltheoretiker John Nash, Nobelpreisträger von 1994. In einer Anfangsszene des Films beobachtet Nash die Bewegungen einer Gruppe von Tauben. Er will Muster darin erkennen und eine Theorie des Verhaltens darauf aufbauen. Mustererkennung kann Nash offenbar besonders gut. Sein Wahrnehmungsapparat ist in dieser Hinsicht sehr empfindlich, bis hin zum Krankhaften. Das führt schließlich dazu, dass er in einer Sammlung von überwiegend belanglosen Zeitungsmeldungen das Muster einer mächtigen Verschwörung findet.

 

Offenbar ist es kein allzu weiter Weg von der wissenschaftlichen Erkenntnis zum Phantasiegebilde und zum Okkulten. Vom Aberglauben und der Esoterik unterscheidet sich die Wissenschaft im Wesentlichen dadurch, dass letztere ihre Vermutungen einer unerbittlichen und nachvollziehbaren Prüfung unterwirft. „Es ist schlechte Wissenschaft, wenn wir unsere Intuitionen und Vorurteile ungeprüft lassen. Im eigenen Interesse sollten wir, wo immer wir das können, die Mängel der intuitiven Schlussfolgerungen aufdecken. Die Methoden der Wissenschaft und der Statistik sind aus dem Widerstand gegen diese Mängel entstanden. Sorgfältig angewendet sind sie unsere beste Waffen gegen derartige Fallen.“ (Goldacre, 2009, S. 255; meine Übersetzung.) Kurz: Bauchentscheidungen sollten unterbleiben, wenn wir es besser wissen können. Wir sollten uns nicht durch bekannte Autoren der populärwissenschaftlichen Literatur irritieren lassen, die mit großem Erfolg das Gegenteil behaupten. Lassen wir diese Bücher dort liegen, wo sie hingehören: in den Esoterik-Ecken der Buchhandlungen.

 

(05.07.2010)

Zurück zur Übersicht

Kausalitätsfalle

Anfang 1995 brachten die Tageszeitungen unter dem Titel Unsicherheitsfaktor Mensch eine Nachricht der Internationalen Zivilluftfahrt-Organisation ICAO: „Als Unsicherheitsfaktor Nummer eins erwies sich auch 1994 wieder der Mensch: Nicht weniger als 31 der 47 Unfälle sind auf  menschliches Versagen zurückzuführen und immerhin 16 auf das Wetter ... Die europäische Airbus Industrie in Toulouse änderte die automatische Steuerung an den A300-600- und A310-Typen.“

Widerspruch. Wenn 31 der 47 Unfälle auf menschliches Versagen und 16 auf das Wetter zurückzuführen sind, kann den Hersteller des Flugzeugs eigentlich keine Schuld mehr treffen. Warum dann die Änderung der automatischen Steuerung?

Analyse. Die Kausalitätserwartung, also die Erwartung, dass es zu jedem Geschehnis eine Ursache gibt, ist ein angeborener Lehrmeister (Konrad Lorenz). Das Kausaldenken ist Grundlage der empirischen Wissenschaften und des freien Willens. Unsere Handlungen erfahren wir als Ursache dessen, was sich daraufhin entwickelt. Dasjenige, was von der getroffenen Entscheidung abhängt, ist die Wirkung. Ursache-Wirkungsbeziehungen sind der Hebel, mit dem es uns gelingt, den Lauf der Welt in unserem Sinne zu beeinflussen. Die Kausalitätserwartung wird von einigen Philosophen sogar zum universell gültigen Prinzip erhoben (Kausalitätsprinzip): Nihil fit sine causa – nichts geschieht ohne Grund. Es wurde bereits von Aristoteles aufgestellt.

Die Suche nach der einen Ursache ist ein so erfolgreiches Prinzip, dass wir uns angesichts eines Geschehnisses erst zufrieden geben, wenn uns eine Ursache genannt wird. Auch ziemlich fadenscheinige Begründungen erfüllen diesen Zweck. Das ist ein wirkungsvoller Ansatzpunkt für die „Meinungskneter“: Der Manipulant braucht diesen mächtigen Drang der Kausalitätserwartung nur zu befriedigen, und zwar so, dass es ihm nützt. Die Kausalitätserwartung wird zur Kausalitätsfalle. Und genau eine solche wird durch die obige Zeitungsmeldung gestellt. Aus Sicht des Herstellers liegt die Schuld an einem Desaster bei den üblichen Verdächtigen: Pilot, Kapitän, Fahrzeugführer. Solche voreiligen Schuldzuweisungen erschweren die unvoreingenommene Suche nach den wirklichen Ursachen. Wir sollten jedem, der von „menschlichem Versagen“ spricht, aufmerksam und kritisch begegnen.

Hier ist ein weiteres Beispiel. Unter der Überschrift „Fehler des Co-Piloten“ meldet die Fuldaer Zeitung vom 27.10.2004: Der Absturz einer Airbus-Maschine in New York kurz nach den Terroranschlägen vom September 2001 ist auf einen Fehler des Co-Piloten zurückzuführen... Zu diesem Schluss kam die US-Untersuchungsbehörde NTSB... Der Co-Pilot habe die Maschine nach Turbulenzen stabilisieren wollen, dabei das Seitenruder des Leitwerks aber falsch bedient. Durch sein aggressives Eingreifen sei das Leitwerk abgefallen.“ (Aus USA Today vom selben Tag erfahre ich von einer Diskussion darüber, dass auch falsches Pilotentraining oder eine Fehlkonstruktion die Hauptrolle gespielt haben könnten.)

Die Wissenschaft hat (noch) nicht für alles kausale Erklärungen parat. Diese unbefriedigte Kausalerwartung beunruhigt manche Menschen so stark, dass sie meinen, einen Urgrund für alles was ist, annehmen zu müssen. Und sie haben auch einen Namen dafür: Gott. Andere drücken sich vorsichtiger aus und sprechen von intelligentem Design (Intelligent Design, ID). Diese Menschen finden Gott – oder eben den intelligenten Designer – dort, wo unsere Erkenntnis Lücken aufweist (God of the Gaps). Das Dumme an diesem heute vor allem in den USA um sich greifenden Glauben ist, dass er im Grunde nichts erklärt. Wir haben es mit einer Denkfalle zu tun. Mehr dazu unter Glaubensfragen. Wer sich dem Thema eher unverkrampft und mit Genuss nähern will, dem empfehle ich das Buch „Roger’s Version“ von John Updike.

Meister der fehlgeleiteten Ursachenforschung sind die Zahlenmystiker. Vermutlich hatte der berühmte Pythagoras weniger Anteil an dem nach ihm benannten Satz als an der Entwicklung der Zahlenmystik. „Auch sie wäre wahrscheinlich ohne ihn entstanden; trotzdem sollte er sich dafür schämen“ (Dudley, 1999).  An vielen Beispielen zeigt Underwood Dudley, auf welche Abwege die Suche nach Sinn im Unsinn führen kann. (Siehe auch die Rätselaufgabe 18 zum Thema „V“ in der Problemsammlung Querbeet.)

(13.04.2005; zuletzt revidiert am 18.01.07)

Zurück zur Übersicht

Glaubensfragen

Es gibt Lebensformen mit Organen hoher Komplexität und wunderbarer Zweckmäßigkeit. Für viele dieser Lebensformen und Organe kennen wir eine schlüssige Stammesgeschichte noch nicht. Hier und da fehlen Verbindungsglieder (Missing Links). Ein gern zitiertes Beispiel ist die der Fortbewegung von Einzellern dienende rotierende Geißel, das Flagellum. Wir wissen noch nicht, aus welchen Vorformen sich dieser Motor hat entwickelt können. Ändert man nur ein winziges Detail oder lässt man eine Kleinigkeit weg, funktioniert der Motor nicht mehr. Im Zuge der Auslese des Bestangepassten aber ist ein nicht rotierender Motor ein Verlustgeschäft. Die Anhänger der Lehre vom Intelligent Design (ID) nennen so etwas irreduzible Komplexität. Sie schließen daraus, dass die Evolutionslehre nach Darwin falsch ist und dass es einen Schöpfer und Steuermann der Welt gibt, einen Urgrund, einen intelligenten Designer, Gott.

Widerspruch. Gott ist da, wo unsere wissenschaftlichen Erklärungen (noch) nicht hinreichen. Er wird von den ID-Anhängern sozusagen in den Lücken unserer Erkenntnis angesiedelt. Für diesen God of the Gaps wird es immer enger. Laufend finden Wissenschaftler neue Verbindungsglieder im Stammbaum des Lebens (Dawkins, 2006; Clack, 2006). Hinzu kommt, dass die Evolution nicht den geraden Weg nimmt. Biologische Mechanismen und Körperteile können in Vorformen andere Funktionen gehabt haben. Wir kennen Zeugnisse für Umwege der Evolution, beispielsweise den blinden Fleck des Auges. Von einem intelligenten Designer wären derartige „Fehlkonstruktionen“ nicht zu erwarten (Dennet, 2005).

Analyse. Die irreduzible Komplexität wird in den USA vor allem von Leuten ins Spiel gebracht, die die biblische Schöpfungsgeschichte als gleichrangig neben der Evolutionslehre im Schulunterricht etabliert sehen wollen. Denn: Die Väter der Verfassung haben (im First Amendment) auf eine strikte Trennung von Staat und Kirche geachtet. Es gibt keinen Religionsunterricht an Schulen. Um die biblische Schöpfungsgeschichte doch noch an die Schulen zu bringen, braucht sie einen wissenschaftlichen Anstrich. Das Aufzeigen von vermeintlich irreduzibler Komplexität und der Schluss auf den dann notwendigen intelligenten Designer wirken bei oberflächlicher Betrachtung wissenschaftlich. Beim nähern Hinsehen ist es aus damit. Die Argumentation zielt auf eine Lähmung der Wissenschaft, die ja geradezu darauf aus ist, Komplexität zu reduzieren. Deshalb machen amerikanische Gerichte hier auch nicht mit. Die Schöpfungslehre bleibt in den meisten Bundesländern aus der Schule verbannt. Aufsehen erregte das Urteil des Richters John Jones, eines von George W. Bush ernannten Lutheraners, das dieser im Dezember 2005 in Pennsylvania verkündete. Der Richter nannte das Intelligent Design eine „atemberaubende Trivialität“, die den Test auf Wissenschaftlichkeit nicht bestehen könne (TIME, 8.5.2006).

Die Frage bleibt, warum das Argument von der irreduziblen Komplexität dennoch auf viele Menschen überzeugend wirkt. Zur Klärung schauen wir uns die Struktur des „Gottesbeweises“ einmal genauer an. Offensichtlich wird angenommen, dass alle möglichen Vermutungen und Hypothesen über die Herkunft eines bestimmten biologischen Sachverhalts (beispielsweise das Flagellum der Einzeller) bekannt sind. Und eine davon ist die Schöpfungshypothese. Wenn nun die bekannten darwinistischen Hypothesen keine befriedigende Erklärung liefern, dann muss die letzte noch verbleibende Hypothese richtig sein: Ein intelligenter Designer war am Werk. Diese Art der Beweisführung wird von den ID-Anhängern eliminierende Induktion (Eliminative Induction) genannt und im Ernst als der wissenschaftlichen Induktion gleichrangig – wenn nicht gar überlegen – angesehen (Dembski, 2003). Dass die Schöpfungshypothese tatsächlich grundsätzlich nicht widerlegbar ist und dass sie allein aus diesem Grunde gar nicht als ernsthafter Konkurrent der wissenschaftlichen Hypothesen gelten kann, scheint die Verfechter der eliminierenden Induktion nicht weiter zu stören.

Nun erkennen wir, warum die eliminierende Induktion für viele so attraktiv ist. Die Offenheit der wissenschaftlichen Arbeit, die ständig drohende Falsifizierung lieb gewonnener Theorien und die fortwährende Suche nach neuen und besseren Hypothesen – all das braucht Personen, die Unsicherheiten aushalten können. Die Umwandlung von Unsicherheit in Sicherheit ist ein ständiger und anstrengender Prozess. Letztendliche Sicherheit, endgültige Wahrheiten sind nicht zu erwarten. Die eliminierende Induktion kommt prätentiös daher. Letztlich ist sie nur Ausdruck der Angstvermeidung, einer Art Kurzschlussreaktion des Neugier- und Sicherheitstriebs. Die eliminierende Induktion macht den beunruhigenden Fragen ein Ende, sie liefert letztgültige Antworten.

Anmerkungen. Die großen Kirchen vertreten die ID-Position wohlweislich nicht. „Christliches Menschenbild und moderne Evolutionstheorien“ ist eine Botschaft von Papst Johannes Paul II. an die Mitglieder der Päpstlichen Akademie der Wissenschaften anlässlich ihrer Vollversammlung am 22. Oktober 1996. Sie beinhaltet einen Vorschlag, wie Glaube und Wissenschaft in Einklang zu bringen sind.

(23.12.06)

Zurück zur Übersicht

Täuschwörter

Das Erfinden und Verbreiten von Täuschwörtern ist ein beliebtes Tätigkeitsfeld von Manipulanten. Meist täuscht nicht das Wort an sich. Die missbräuchliche Verwendung macht’s.

Entsorgungspark (statt Müllkippe)

Freisetzung (statt Entlassung)

Verschlankung (statt Stellenabbau)

Neuartiger Waldschaden (statt Waldsterben)

Nullwachstum (statt Stagnation)

Restrisiko (statt Risiko)

Sicherheitsrelevanter Ausfall (statt gefährlicher Ausfall)

Verteidigungsministerium (statt Kriegsministerium)

Nichtrückzahlbare Anleihe (statt: verlorener Zuschuss)

Schadensqualität (statt Gift)

Polizist „gibt drei Schüsse ab“, der Verfolgte „stirbt auf der Stelle“ (statt: Polizist erschießt den Verfolgten)

Der Kanzler „bekräftigte die ‚europäische Perspektive‘ Bulgariens“. So lässt sich mit bedeutungsschweren Wörtern nichts sagen.

Sanfte Kundendaten (statt Kundenausspähung)

Recht auf humanitäre Einmischung (Kriegsgrund). Kommentar: Man traue keinem erhabenen Motiv, wenn sich auch ein niedriges finden lässt.

Kollateralschaden (für die zivilen Opfer eines Krieges)

Fehler (statt Lüge): Roland Koch, Hessischer Ministerpräsident im Januar 2000; er deklarierte Gelder aus schwarzen Kassen als Darlehen. Wem der Un­terschied nicht klar ist: Fehler passieren einem schon einmal, Lügen dagegen nicht.

Die USA setzen auf „fließenden Sieg“ (Tageszeitung, 7.4.03). Planer haben monatelang lang an einer Definition eines Sieges in diesem Kriegsfall gearbeitet.

Verteidigung der Menschenrechte (noch ein Kriegsgrund) – Wie gesagt: Die missbräuchliche Verwendung macht’s.

Lebensmitteltechnisch optimiert (für genmanipulierte Lebensmittel)

Analyse. Die Wirkung der Täuschwörter beruht auf dem Denkmechanismus der unbewussten Assoziationen.

(07.02.12)

Zurück zur Übersicht

Veröffentlichungen

Grams, T.: Grundlagen des Qualitäts- und Risikomanagements. Zuverlässigkeit, Sicherheit, Bedienbarkeit. Vieweg Praxiswissen, Braunschweig, Wiesbaden 2001 (Skriptum)

Grams, T.: Denkfallen beim objektorientierten Programmieren. it 34(1992)2, 102-112

Grams, T.: Denkfallen und Programmierfehler. Springer Compass, Berlin, Heidelberg 1990

Grams, T.: Ursachen häufiger Programmierfehler. Handbuch der modernen Datenverarbeitung HMD (Nov. 1988) Heft 144 „Fehlertolerante Systeme“, 46-57

Grams, T.: Thinking Traps in Programming - A Systematic Collection of Examples. SAFECOMP '88. IFAC Proceeding Series 1988, Number 16. Pergamon Press, 95-100

Grams, T.: Biased Programming Faults - How to Overcome Them? Aus: Informatik-Fachberichte 147 (Hrsg.: F. Belli, W. Görke) Fehlertolerierende Rechensysteme, 1987, 12-23

Siehe auch unter

Zurück zur Übersicht

Literaturhinweise

Anderson, John R.: Kognitive Psychologie. Heidelberg 1988

Beck-Bornholdt, Hans-Peter; Dubben, Hans-Hermann: Der Hund, der Eier legt. Erkennen von Fehlinformation durch Querdenken. Rowohlt Taschenbuch Verlag, Reinbek bei Hamburg 2001. Eine solide Darstellung und Analyse der wesentlichen statistischen Denkfallen.

Boltzmann, L.: Populäre Schriften. Ausgewählt von Engelbert Broda. Vieweg, Braunschweig 1979

Bördlein, Christoph: Das sockenfressende Monster in der Waschmaschine. Eine Einführung ins skeptische Denken. Alibri, Aschaffenburg 2002

Carnap, Rudolf; Stegmüller, Wolfgang: Induktive Logik und Wahrscheinlichkeit. Springer, Wien 1959

Clack, Jennifer A.: Was Fischen Beine machte. Spektrum der Wissenschaft (2006)10, 24-32

Dawkins, Richard: The God Delusion. London 2006

Dembski, William, A.: “Science and Design” + “The Logical Underpinnings of Intelligent Design”. Professorenforum-Journal 2/2003

Dennet, Daniel C.: Intelligent Design – Wo bleibt die Wissenschaft? Spektrum der Wissenschaft (2005) 10, 110-113

Dörner, Dietrich: Problemlösen als Informationsverarbeitung. Kohlhammer, Stuttgart 1979

Dudley, Underwood: Die Macht der Zahl. Was die Numerologie uns weismachen will. Birkhäuser, Basel 1999 (Original: Numerology – Or, What Pythagoras Wrought. Washington 1997)

Dueck, Gunter: Ein Indikatorenhoch über Deutschland! Starke Triebwinde. Informatik Spektrum 26 (2003) 1, S. 39-44

Ehrenberger, W.: Software-Verifikation. Verfahren für den Zuverlässigkeitsnachweis von Software. Hanser, München, Wien 2002

Evans, Jonathan St. B. T.: Bias in Human Reasoning: Causes and Conse­quen­ces. Lawrence Erlbaum Associates, Publishers, Hove and London (UK)  1989

Fisz, Marek: Wahrscheinlichkeitsrechnung und mathematische Statistik. DVW Berlin 1976

Goldacre, Ben: Bad Science. Harper Collins, London 2009

Hell, Wolfgang; Fiedler, Klaus; Gigerenzer, Gerd (Hrsg.): Kognitive Täuschungen. Spektrum Akademischer Verlag, Heidelberg, Berlin, Oxford 1993

Huff, Darrell: How to lie with statistics. 1954, 1982. Der Klassiker zum Thema Statistikplunder.

Kahneman, Daniel; Slovic, Paul; Tversky, Amos (eds.): Judgment under uncertainty: Heuristics and biases. Cambridge University Press, Cambridge CB2 1RP, 1982

Kleinrock, Leonard: Queuing Systems. Vol. 1: Theory. Wiley-Interscience 1975

Krämer, Walter: So lügt man mit Statistik. Campus, Frankfurt/M. 1991

Krech, Crutchfield u. a.: Grundlagen der Psychologie. Band 4 Kognitionspsychologie. Beltz, Weinheim 1992. (Vorstellungen und Denken, S. 109)

Leiter, Brian: Why Tolerate Religion? University of Texas, Austin, 25.05.2006

Papoulis, Athanasios: Probability, Random Variables, and Stochastic Processes. McGraw-Hill, New York 1965

Pólya, Georg: Schule des Denkens. Francke, Bern 1949

Popper, Karl R.: Conjectures and Refutations. The Growth of Scientific Knowledge. Routledge, London 1963 (Deutsch: Vermutungen und Widerlegungen. J. C. B. Mohr, Tübingen  1994/1997)

Poundstone, William: Labyrinths of Reason. Anchor Book, New York 1988

Randow, Gero von: Das Ziegenproblem. Denken in Wahrscheinlichkeiten. Rowohlt Taschenbuch Verlag, Reinbek bei Hamburg 2004. Ausführliche Behandlung des Drei-Türen-Problems. Das Buch kann auch als Einführung in die elementare Wahrscheinlichkeitsrechnung gelesen werden.

Sachs, Lothar: Angewandte Statistik. Anwendung statistischer Methoden. Springer, Berlin, Heidelberg 1992

Sainsbury, R. M.: Paradoxes. Cambridge University Press, 1995 (deutsch: Paradoxien. Reclam, Stuttgart 2001)

Schönwandt, Walter: Denkfallen beim Planen (Ausarbeitung eines Referats)

Stewart, Ian: Mathematische Unterhaltungen (Wie eine verblüffende Möglichkeit, aus einer scheinbar ganz nutzlosen Information Vorteil zu ziehen, die Gemüter jenseits und diesseits des Atlantiks bewegte.) Spektrum der Wissenschaft (1991) 11, 12-16

Székely, Gábor J.: Paradoxa. Klassische und neue Überraschungen aus Wahrscheinlichkeitsrechnung und mathematischer Statistik. Harri Deutsch, Thun, Frankfurt am Main, 1990

Thomas Waschke (2003): Intelligent Design – Eine Alternative zur naturalistischen Wissenschaft? Skeptiker 4/2003

Tversky, Amos; Kahnemann, Daniel: Judgment under Uncertainty: Heuristics and Biases. Science 185 (Sept. 1974), 1124-1131 (Auch enthalten in: Kahneman, Slovic, Tversky, 1982)

Urban, Martin: Wie die Welt im Kopf entsteht. Von der Kunst, sich eine Illusion zu machen. Eichborn, Frankfurt/M. 2002. Aus dem Inhalt: Logik des Aberglaubens. Bilder als Machtinstrument der Kirche. Magie der Medien.

Watzlawick, Paul; Beavin, Janet H.; Jackson, Don D.: Menschliche Kommunikation. Formen, Störungen, Paradoxien. Verlag Hans Huber, Bern 1969

 Zurück zur Übersicht

Verbindungen

Allgemein

Rätsel und Rechenaufgaben

Anschauungsmaterial zum Thema Denkfallen bieten Rätsel und Rechenaufgaben, die in verschiedenen Sammlungen erschienen sind (beispielhaft: Walther Lietzmanns Buch „Wo steckt der Fehler“, die Kolumnen von Martin Gardner und Ian Stewart im Spektrum der Wissenschaft), die Web-Seite von David Eppstein.

Wandersagen und Stadtlegenden

Die Sinnsuche des Wahrnehmungs- und Denkapparats lässt uns auch in Nichtssagendem („Schröder [der Kanzler] bekräftigte die 'europäische Perspektive' Bulgariens.“) und fadenscheinigen Geschichten irgend einen Sinn erkennen. Beispiele bieten die Astrologie und die Wahrsagerei - aber auch die vielen Wandersagen und Stadtlegenden. Hier sind Verbindungen zu Sammelstellen für solche Wandersagen:

 Zurück zur Übersicht

© Timm Grams, 1998-2015, aktualisiert am 22.05.2020 (Weitere Beispiele finden Sie im Weblogbuch Hoppla!)