Agenda 2000: Fewer sheep mean higher profits

Umweltsimulation mit Tabellenkalkulation

Studie zum Thema "Ressourcenschonung, Subventionen und Direktbeihilfe"

Vorbemerkung

Die Studie ist für fortgeschrittene Teilnehmer des Kurses Umweltsimulation mit Tabellenkalkulation gedacht. Der folgende Text ist ein Leitfaden zur Erstellung des mathematischen Modells. Das Computermodell wird mittels Tabellenkalkulation realisiert. (Ein Arbeitsblatt, das Ergebnis der Studie ist, kann übers Netz geladen werden.)

Einführung

"How to wean farmers from an over-dependence on subsidies from the E.U.'s bloated Common Agricultural Policy? In New Zealand, farmers themselves advocated the sweeping cuts. They realized that grazing 70 million subsidized sheep had caused a drop in breeding standards and serious environmental damage. There were too few buyers - a lot of sheep were ground up for fertilizer - and subsidies bled the public purse. So the main industry group, the Federated Famers, proposed to the incoming Labour government in 1984 that subsidies be slashed and protection removed. Overnight, farmers were forced to become super-efficient and market-driven. An example of their success is that today sheep numbers have dropped to 47 million, but the country earns 30% more in real terms from those animals than it did when there were 70 million... Lockwood Smith, until recently New Zealand's Agriculture Minister: 'Removing subsidies has given us far better environmental outcomes, and far better economic ones.'" (Robinson, Winter 1998/99).

Der Agrarpolitiker - oder Wirtschaftspolitiker - hat es mit einer Reihe von miteinander konkurrierenden Zielen zu tun:

Versorgung der Bevölkerung mit erschwinglichen Gütern.

Sicherung des sozialen Friedens - eventuell durch Umverteilung zugunsten der Armen.

Sicherung der Produktion durch ausreichende Bezahlung der Produzenten (Landwirtschaft ist Lebensgrundlage der Bevölkerung).

Schonung der Ressourcen durch nachhaltiges Wirtschaften (Sustainablility).

Wie ist das alles unter einen Hut zu bringen? Eine einfache Computersimulation soll die wichtigsten Zusammenhänge klar machen und eine Bewertung der verschiedenen Politiken ermöglichen.

Das Modell des Marktes

Annahmen (vollkommener Markt): Wir gehen bei der Modellbildung von einem bestimmten Gut (zum Beispiel Schafe) aus und betrachten das Marktgeschehen für dieses eine Produkt. Wechselwirkungen mit anderen Märkten und Produkten bleiben also unberücksichtigt. Es werden aggregierte Größen betrachtet, also Summengrößen für Nutzen, Wert und Kosten (Makromodellierung). Das Marktgeschehen wird von vollständig informierten Produzenten und Konsumenten bestimmt. Von der Ungleichverteilung der Einkommen wird abstrahiert. (Allerdings kann man an der Gesamtproduktion sehen, ob auch die Ärmeren mit dem Gut versorgt werden.) Die Produzenten agieren unter denselben Bedingungen und versuchen den Gesamtgewinn zu maximieren (Quasi-Monopol).

Die Kenngrößen des Modells:

x Gesamtproduktion (auch: Ertrag) - von der Zeit t abhängig: x = x(t)

A Höchstpreis

B Sättigungsmenge

p(x) Marktpreis

a Fixkosten

b variable Kosten

c Kostenfaktor für Übernutzung

Q(x) Kosten, die den Produzenten insgesamt entstehen

V(x) Konsumsumme (Kosten, die den Verbrauchern insgesamt entstehen; Wert, den die Produzenten insgesamt erhalten)

U(x) Zahlungsbereitschaft der Verbraucher (auch: Nutzen des Gutes für die Verbraucher)

s Subvention je Exemplar

S(x) Subventionen insgesamt

D Direktbeihilfe insgesamt

G(x) Förderung insgesamt (Staatsausgaben)

K Kapazität des Marktes

B_p(x) Produzentenbilanz, Gewinn (Konsumsumme + Förderung - Kosten)

B_c(x) Verbraucherbilanz, Konsumentenrente (Nutzen - Konsumsumme - Förderung)

Die Systemgleichungen: Für den Stückpreis in Abhängigkeit von der Gesamtproduktion machen wir den Ansatz

(Preisformel)

Für den Produzenten bestimmt der Preis den Wert des Produkts. Der gesamte Wert ist demzufolge gleich

(Wertformel)

Der Preis bestimmt den Grenznutzen. Das ist der Nutzen, den - bei einer bestimmten gegebenen Produktion x - eine zusätzlich prodzierte Einheit für den Verbraucher hat und der dafür diesen Preis gerade noch bezahlen würde. Die Preisformel ist demzufolge ein Ansatz, der das Gesetz vom abnehmenden Grenznutzen auf einfachste Art wiederspiegelt. Der Gesamtnutzen U(x) einer Produktion x ergibt sich als Integral über den Grenznutzen (oder umgekehrt: der Grenznutzen ist gleich der Ableitung des Gesamtnutzens). Also:

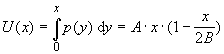(Nutzenformel)

Die Gesamtkosten setzen sich hier zusammen aus einem Fixkostenanteil a und den variablen Kosten. Für die Stückkosten des variablen Anteils wird der Ansatz b + c× x gemacht. Also: b sind die konstanten Stückkosten und c× x gibt den steigenden Stückkostenanteil wieder, der auf die Übernutzung der Ressourcen (Überweidung und dergleichen) zurückgeht. Daraus folgt die Kostenformel

(Kostenformel)

Die gesamten Subventionen sind gleich S(x) = s x. Die staatliche Förderung beläuft sich insgesamt auf

(Förderung)

Die Einkommensbilanz aller Produzenten ist

(Produzentenbilanz)

Die Nutzenbilanz über sämtliche Verbraucher ist

(Verbraucherbilanz)

Das dynamische Modell: Die Gesamtproduktion ist zeitabhängig: x = x(t). Für das Wachstum der Produktion machen wir mit der bestandsabhängigen Zuwachsrate r(x) den Ansatz

(Wachstumsgleichung)

Hierin steht "x Punkt" für die Änderungsgeschwindigkeit dx(t)/dt der Gesamtproduktion.

Für die Bestimmung der Zuwachsrate gehen wir davon aus, dass die Produzenten ihren Gewinn maximieren wollen. Die Veränderung der Produzentenbilanz aufgrund einer zusätzlich produzierten Einheit stellt den Anreiz für die Produktion dar. Ist diese Veränderung positiv, wird mehr produziert. Ein Rückgang der Produzentenbilanz, also eine Wertminderung, zieht einen Rückgang der Produktion nach sich. Es ist also gerechtfertigt, die Zuwachsrate proportional zur Änderung der Produzentenbilanz (bezogen auf eine Einheit) anzusetzen. Diese Änderung ist gleich der Ableitung der Produzentenbilanz nach der Gesamtproduktion. Mit den Proportionalitätskonstanten k und R ist die bestandsabhängige Zuwachsrate gleich

(Zuwachsrate)

Die dynamischen Gleichungen laufen also auf ein begrenztes Wachstum (auch: logistisches Wachstum) einer einzelnen Population hinaus. Die Proportionalitätskonstante R hat keinen wesentlichen Einfluss auf das allgemeine Verhalten des Prozesses und kann nach rein numerischen Gesichtspunkten bestimmt werden. Die Kapazität des Marktes K ist gleich dem sich langfristig einstellenden Gleichgewichtswert der Gesamtproduktion:

Sie ist gegeben durch

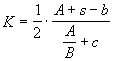(Kapazität)

Ergebnisse der Simulationsexperimente

Das Simulationsmodell ist im Arbeitsblatt FewerSheep der Excel-Datei Growth.xls realisiert. Mit dem Arbeitsblatt wurden eine Reihe von Experimenten durchgeführt. Die wichtigsten Ergebnisse sind in Tabelle 1 und Bild 1 wiedergegeben. Die Schlussfolgerungen lassen sich folgendermaßen zusammenfassen:

Am freien Markt kriegt nicht jeder, was er will. Der freie Markt verhindert die vollkommene Marktversorgung.

Unvollkommene Marktsättigung trifft die Armen stärker als die Reichen. Die Ungleichverteilung der Einkommen bleibt im objektiven und auf aggregierte Wertgrößen zurückgeführten Wertbegriff unberücksichtigt. Der sich am Markt einstellende Grenznutzen (=Wert=Preis) macht für den Armen eine Sache unerschwinglich, die ein Reicher ohne weiteres genießen kann.

Subventionen bewirken - bei progessiven Steuersätzen - aufgrund der besseren Marktversorgung eine Umverteilung zugunsten der Armen.

Subventionen gehen stets zu Lasten der Gesamtheit der Verbraucher.

Die "Sozialisierung des Luxus" wird mit dem Zusammenbruch der Ökosysteme bezahlt. (Das liegt daran, dass die Kapazität des Marktes K gleichermaßen Indikator für die Marktversorgung und die Umweltbelastung ist.)

Direktbeihilfe verbessert nicht die Marktversorgung.

Direktbeihilfe kann sowohl die Gesamtbilanz der Verbraucher als auch die der Produzenten verbessern.

Direktbeihilfe schont die Ressourcen und verschlechter gleichzeitig die Marktversorgung. Also: Ressourcenschonung geht zu Lasten der Armen.

Man kann den Kuchen nicht gleichzeitig haben und essen.

Politikänderungen können vorübergehend Effekte nach sich ziehen, die dem angestrebten Ziel zuwiderlaufen (Übergangsvorgänge).

Tabelle 1 Experimente mit dem Arbeitsblatt FewerSheep (Growth.xls)

Parameter und Resultate	Experimente
Parameter und Resultate	1	2	3	4	5	6
A	100	100	100	100	100	100
B	100	100	100	100	100	100
a	0	0	0	0	0	0
b	0	0	0	0	0	0
c	0	0	2	2	2	2
s	0	80	0	80	0	50
D	0	0	0	0	2000	820
K	50	90	16.7	30	16.7	25
B_p	2500	8100	833	2700	2833	2695
B_c	1250	-3150	139	-1950	-1861	-1758

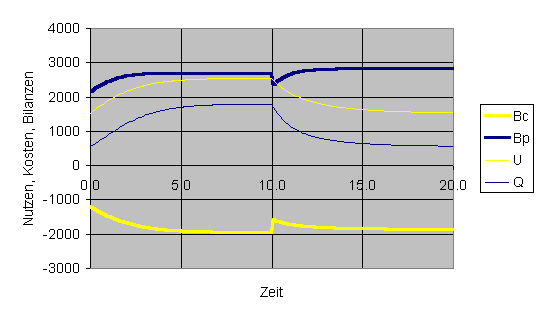
Bild 1 Wachstumsprozesse und Übergangsvorgänge bei Politikänderungen
(Start mit dem Endzustand des 3. Experiments, in der Zeit von 0 bis 10 gelten die Parameterwerte des 4. Experiments und von 10 bis 20 die des 5. Experiments)

Literaturhinweise

Hillebrand, K.: Elementare Mikroökonomik. Fulda 1992. Angebots-, Nachfrage- und Kostenfunktion, Ertragsgesetz, Höchstpreis, Sättigungsmenge, Stückkosten.

Neubäumer, R.; Hewel, B. (Hrsg.): Volkswirtschaftslehre. Grundlagen der Volkswirtschaftstheorie und Wirtschaftspolitik. Gabler, Wiesbaden 1998. Kostenfunktion (S. 75), vollkommener Markt (S. 96), Konsumsumme, Zahlungsbereitschaft, Konsumentenrente (S. 101)

Odum, E. P.: Prinzipien der Ökologie. Lebensräume, Stoffkreisläufe, Wachstumsgrenzen. Spektrum der Wissenschaft, Heidelberg 1991. Populationswachstum. Kapazität des Lebensraumes.

Paulsen, A.: Allgemeine Volkswirtschaftslehre. Band I. de Gruyter, Berlin, 1970

Robinson, S.: The Kiwi Solution. (Fewer sheep mean higher profits.) TIME, special issue, Winter 1998/99, Vision of Europe, p. 100

Stobbe, A.: Gesamtwirtschaftliche Theorie. Springer, Berlin, Heidelberg, New York 1975

Wilson, E. O.; Bossert, W. H.: Einführung in die Populationsbiologie. Springer, Berlin, Heidelberg, New York 1973. Elementare mathematische Modelle für Populationswachstum: exponentielles und begrenztes Wachstum, Zuwachsrate, Kapazität der Umwelt.