Umweltsimulation mit Tabellenkalkulation

Quasi-Spezies: Stabilität und Variabilität in der Evolution

Einführung

Es geht erneut um die Mechanismen der Evolution und um die Simulation des Selektionsprozesses, also um die ökologische Simulation. (Eine erste Einführung bietet die Lektion zum Falke-Tauben-Spiel.) Eine der zentralen Fragen der Evolutionslehre ist, wie das Neue entstehen und sich etablieren kann. Einerseits wird von den Mustern oder Genen Stabilität gefordert, also ein gewisser Dogmatismus bei der Aufrechterhaltung von Mustern. Andererseits sind Variabilität und Abweichungen von der Norm unerlässlich für die Anpassung an veränderte Bedingungen und für die Entstehung des Neuen. Manfred Eigen ist dieser Frage nach dem rechten Maß von Stabilität einerseits und Variabilität andererseits nachgegangen. Sein Quasi-Spezies-Modell liefert ein paar gute Antworten. Bereits eine einfache Tabellenkalkulation macht das Wesentliche des Modells deutlich.

Das Modell

Wir betrachten Populationen von Individuen, deren Erscheinungsformen und Verhalten durch Informationen festgelegt sind, die als einfache Bitfolgen der Länge n vorliegen mögen. Diese Bitfolgen nennen wir hier einmal Muster. Jedem dieser Muster können wir nach den Regeln der Dualcodierung eine Zahl zuordnen: die Bitfolge 0…000 entspricht der Zahl 0, die Folge 0…001 der Zahl 1, die Folge 0…010 der Zahl 2, die Folge 0…011 der Zahl 3 usw.

Die Umwelt setzen wir als konstant voraus und in dieser Umwelt hat jedes Individuum eine Lebenserwartung und eine Chance auf Nachkommen, die allein von seinem Programm – dem Muster – abhängen möge. Jedes der Muster i hat also eine gewisse Geburtenrate (Replication Rate) A_i und eine Sterberate (Degredation Rate) D_i.

Manfred Eigen untersucht den Fall sehr langer Muster. Denn in der Natur geht die Länge der Muster des genetischen Materials in die Milliarden. Aber bereits mit Bitmustern der Länge n gleich tausend übersteigt die Zahl der möglichen Muster die Anzahl der Atome im Universum bei weitem. In einer jeden Populationsmenge kann also nur ein winziger Teil aller möglichen Muster überhaupt vorhanden sein. Dennoch sollten im Selektionsprozess optimale Muster, auch wenn sie in der Anfangspopulationsmenge gar nicht vorkommen, relativ zügig dominant werden können. Wie kann das gehen?

Zur Erläuterung betrachten wir einen einfachen Fall, der mittels Tabellenkalkulation durchgerechnet werden kann. Die Muster beschränken wir auf eine Länge von n = 3. Es gibt also acht verschiedene Muster, die wir mit den Zahlen von 0 bis 7 bezeichnen wollen: 0 (000), 1 (001), 2 (010), 3 (011), 4 (100), 5 (101), 6 (110), 7 (111). Wir ordnen die Muster so an, dass sich benachbarte Muster in nur einem Bit unterscheiden: 0, 1, 3, 2, 6, 7, 5, 4. Mit d(i, j) bezeichnen wir die Anzahl der Bits, in denen sich die Muster i und j unterscheiden (das ist die so genannte Hamming-Distanz der Muster). Bei der Replikation möge das Muster des Elters auf das Kind übergehen. Dabei können Kopierfehler (Mutationen) auftreten. Wir nehmen an, dass die Fehler auf den einzelnen Bitpositionen voneinander statistisch unabhängig sind und dass sie die Wahrscheinlichkeit p besitzen. Das ist die Kopierfehlerwahrscheinlichkeit, manchmal auch Fehlerrate genannt. Die Wahrscheinlichkeit der Kopiertreue bezeichnen wir mit q. Es ist q = 1- p.

Die Wahrscheinlichkeit Q_ij, mit der das Muster j einen Nachkommen mit dem Muster i erzeugt, ergibt sich damit zu . Wir definieren die Matrix der Wachstumsraten W_ij folgendermaßen: W_ii = Q_ii∙A_i –D_i und W_ij = Q_ij∙A_j für j≠i. Die Wachstumsgeschwindigkeit der Population des Musters i hängt von der Größe sämtlicher Populationen ab. Bezeichnen wir die Populationsgröße der Individuen mit dem Muster i mit N_i, dann ist die Wachstumsgeschwindigkeit der Population i gegeben durch . Ganz analog zum Falke-Taube-Spiel wird auch hier die Rechnung für die Populationsanteile x_i durchgeführt: . Der Wachstumsprozess für die hier betrachteten acht Muster wird mit endlicher Zeitschrittweite im Tabellenkalkulationsblatt QuasiSpecies.xls durchgerechnet.

Ein Experiment

In der folgenden Tabelle sind die Geburts- und Sterberaten der betrachteten Populationen wiedergegeben. Anfangs gibt es nur Vertreter des Musters Nummer 7. Dieses Muster ist am weitesten weg vom Muster Nummer 0. Letzteres hat die höchste Geburtenrate und müsste sich im Wettbewerb der Muster letztlich durchsetzen.

Muster	0	1	3	2	6	7	5	4
Geburtenrate	1	0.9	0.9	0.9	0.9	0.9	0.9	0.9
Sterberate	0	0	0	0	0	0	0	0
Anfangsgröße der Populationen	0	0	0	0	0	1	0	0

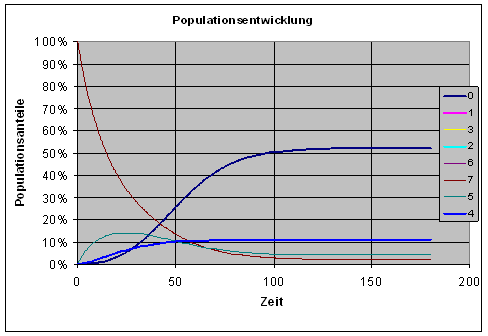
Und genau das passiert auch mehr oder weniger schnell, in Abhängigkeit vom Parameter p, der Kopierfehlerwahrscheinlichkeit. Nicht überraschend ist, dass sich der Endzustand bei größerem p schneller einstellt als bei kleinem p. Die folgende Grafik zeigt die Entwicklung im Falle der Kopierfehlerwahrscheinlichkeit p = 0.02.

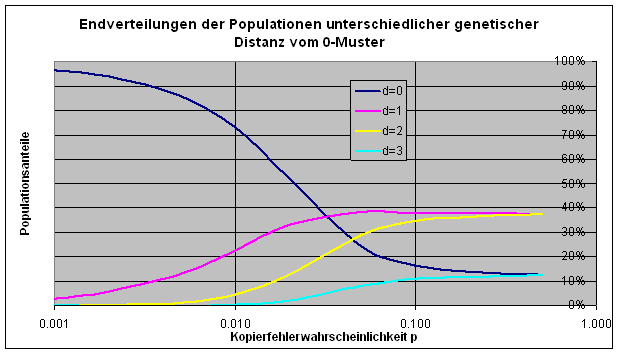
Noch wesentlich interessanter ist, wie sich die Populationen am Ende verteilen. Dass 0-Muster verliert mit zunehmendem p an Dominanz, wie die folgende Grafik der Endzustände zeigt. (In der Grafik sind alle Individuen, deren Muster einen bestimmten Abstand vom 0-Muster haben, zu einer Population zusammengefasst.)

„Im stationären Zustand, der schließlich erreicht wird, existiert der stärkste Teilnehmer, der als Stammsequenz bezeichnet wird, in Gemeinschaft mit allen Mutantensequenzen, die aus der Stammsequenz durch fehlerhaftes Kopieren hervorgegangen sind. Diese Verteilung von Sequenzen bezeichnen wir als Quasi-Spezies“ (Eigen/Gardiner/Schuster/Oswatitsch, 1981). Das 0-Muster in unserem Experiment ist in dieser Terminologie die Stammsequenz der Quasispezies.

Ab einer Kopierfehlerwahrscheinlichkeit von etwa p = 0.04 kann man überhaupt nicht mehr von Dominanz reden: Das 0-Muster „geht im Chaos unter“. Das macht deutlich, welche Rolle die Stabilität im kreativen Prozess spielt. Bei kleinem p braucht das Neue zu lange und bei Überschreitung einer gewissen Fehlerschranke ist Selektion nicht mehr möglich und das Neue kommt gar nicht.

Bei größerer Länge der Muster wird der Übergang vom Selektionsbereich in das Chaos noch viel prägnanter. Das kann man sich in der Originalarbeit von Eigen, McCaskill und Schuster (1988) ansehen. Für eine Simulation dieser Fälle ist die Tabellenkalkulation nicht mehr geeignet. Man geht am besten auf eine universelle Programmiersprache über, beispielsweise auf Java.

Literaturhinweise

Eigen, Manfred; McCaskill, John; Schuster, Peter: Molecular Quasi-Species. The Journal of Physical Chemistry 92 (1988) 24, 6881-6891

Eigen, Manfred; Gardiner, William; Schuster, Peter; Winkler-Oswatitsch, Ruthild: Ursprung der genetischen Information. Spektrum der Wissenschaft (1981) 6, 36-56

Eigen, Manfred: Virus-Quasispezies oder die Büchse der Pandora. Spektrum der Wissenschaft (1992) 12, 42-55

Zurück zur Gliederung

© Timm Grams, 29.03.2008