Problemlösen
|
|
Java-Demo-Projekte. Vollständig dokumentiert. Frei verfügbare Quelltexte.
Irrtümer, den schöpferischen Prozess betreffend
Irrtum 1: Der schöpferische Prozess ist Teamwork
Schauen wir uns doch einmal an, was die wirklich erfolgreichen Erfindungen sind, solche, die noch heute unser Leben bestimmen: Der Zufall steht am Anfang und der trifft eine Person: Das Genie, das die Chance erkennt, das über den nötigen Eifer und eine gehörige Portion Ausdauer zur Umsetzung seiner Idee verfügt. Eine Person. Natürlich mag sie große Lehrer gehabt haben. Und oft findet man ein fruchtbares Umfeld. Aber kaum jemals wird ein Team zielstrebig zu einer wegweisenden Erfindung kommen.
Teams eignen sich prima für Routineaufgaben, für die Aktivierung des bereits Gewussten, als ausführende Organe im Gefolge großer Ideen, nicht aber für die Hervorbringung derselben. Auch als Treibhäuser für Genies sind sie geeignet. Aber es stimmt nun einmal: Hundert kluge Köpfe bringen nicht hundertmal klügere Ideen zum Vorschein als einer allein. Der Geistesblitz ereignet sich notgedrungen in einem einzigen Kopf.
Von Niklaus Wirth wissen wir, dass er sich aus den Gremien zurückzog, deren Ziel die Schaffung einer Nachfolgerversion der Programmiersprache Algol sein sollte (Böszörményi, Gutknecht, Pomberger, 2000). Er schuf die elegante und schlanke Programmiersprache Pascal. Und diese Sprache hatte großen Einfluss auf die weitere Entwicklung der Informatik.
Auch Konrad Zuse hat den Computer allein in seinem Kopf ersonnen. Als ein Nachbau des Zuse-Rechners Z1 für das technische Museum in Berlin anstand, musste er selbst – obwohl bereits in sehr hohem Alter – diese Sache in die Hand nehmen. Keiner sonst kannte sich gut genug damit aus.
Irrtum 2: Das Neue ist planbar
Von Ludwig Boltzmann ist der Aphorismus: „Nirgends weniger als in den Naturwissenschaften bewahrheitet sich der Satz, dass der gerade Weg der kürzeste ist.“ Die Alchimisten richteten all ihre Anstrengungen auf die Herstellung von Gold – und sie schufen etwas gewaltiges Neues: unsere Chemie. Gold kam nicht dabei heraus.
In Wildwestfilmen spielen Telegraphen zuweilen eine Schlüsselrolle. Sie erinnern sich an John Fords Film „Stage Coach“. Allerdings brauchte man bis in die zweite Hälfte des neunzehnten Jahrhunderts hinein für jede Kommunikationsverbindung zwischen zwei Stationen und für jede Übertragungsrichtung ein extra Kabel. Abhilfe versprach der Mehrfachtelegraph, mit dem sich riesige Kabelmengen würden einsparen lassen. Tatsächlich suchten damals viele Leute nach einer technischen Lösung, unter ihnen Elisha Gray und Alexander Graham Bell. Gray war als Ingenieur und Teilhaber eines Telegraphenherstellers professionell mit der Suche nach dem Mehrfachtelegrafen befasst. Seine Versuchsapparaturen entsprachen den technischen Standards. Bell hingegen war als Amateur unterwegs. Sein eigentliches Gebiet war die Sprecherziehung. Seine Apparate waren eher Bastelarbeiten (Hounshell, 1981).
Aber zweierlei widerfuhr beiden: Erstens blieb ihre Suche nach dem Mehrfachtelegraphen erfolglos, und zweitens fanden beide unabhängig voneinander und durch puren Zufall, dass man mit den Apparaten telefonieren kann. Bei Bell beispielsweise war es ein spontaner Einfall als er zwei Jungen zusah, die mit einer Art „Dosentelefon“ spielten. Er dachte sich ein elektrisches Analogon zu den schwingenden Dosenböden und dem Übertragungsmedium Schnur aus.
Die wesentlichen Revolutionen rund um das Internet sind Leistungen Einzelner und sie haben mit dem jeweils aktuellen Hauptstrom oder mit den offiziellen Wissenschaftsprojekten nicht viel zu tun. So war es auch bei der Erfindung des World Wide Web durch den Engländer Tim Berners-Lee.: „Ein Problem am CERN war, dass sich ein Teil der Laboratorien auf französischem Gebiet befand, ein anderer Teil auf schweizerischem... In den beiden Ländern herrschte eine unterschiedliche Netz-Infrastruktur, die den Austausch von Informationen erschwerte, wenn nicht unmöglich machte. 1989 schlug Berners-Lee seinem Arbeitgeber CERN ein Projekt vor, das auf dem Prinzip des Hypertexts beruhte und den weltweiten Austausch sowie die Aktualisierung von Informationen zwischen Wissenschaftlern vereinfachen sollte. Er verwirklichte dieses Projekt und entwickelte dazu den ersten Browser… Dies sollte den Ursprung des World Wide Webs darstellen.“ (Wikipedia, 30. März 2009)
Manchmal geht es noch weitaus dramatischer zu. „Menschliches Versagen“ ist im Spiel. Aus gutem Grund setze ich den Begriff „menschliches Versagen“ stets in Anführungszeichen. Denn: Fehler machen gehört zu den wichtigen Fähigkeiten des Menschen. Er ist kein Automat. Viele Erfindungen und Entdeckungen wären ohne Regelverstöße oder Fehler nicht zustande gekommen. Elisha Gray kam nämlich erst auf die entscheidende Idee, als sein Neffe den Versuchsaufbau des Mehrfachtelegrafen zweckwidrig mit der Zinkbadewanne verbunden hatte und die elektrischen Schwingungen dadurch hörbar wurden.
Die Geschichte der Bahn brechenden Neuerungen ist voll mit Fällen „menschlichen Versagens“: Galileo Galilei hat ein Spielzeug zweckentfremdet, es sozusagen bestimmungswidrig gen Himmel gerichtet. Dabei hat er die Jupitermonde, die Saturnringe und die Venusphasen entdeckt – und unser Weltbild grundlegend verändert. Alexander Fleming bemerkte nach einem Urlaub, dass einige seiner Bakterienkulturen verdorben waren. In der Folge kam es zur Entdeckung des Penicillins.
Das Leben spielt sich im Spannungsfeld zwischen Dogmatismus und Regellosigkeit ab. Und dort entsteht das Neue.
Irrtum 3: Allein auf den guten Einfall kommt es an
Zufall oder gar Fehler sind unabdingbar für das Zustandekommen des Neuen. Aber das ist erst die Hälfte der Geschichte. Gray maß seiner Entdeckung nur geringe Bedeutung bei. Er betrieb die Patentanmeldung ohne Nachdruck. Er war wohl zu stark auf sein von der Profession bestimmtes Ziel fixiert, auf den Mehrfachtelegraphen. Anders Bell: Als Fachmann für Sprache wurde ihm die Bedeutung seiner Erfindung völlig bewusst. Er klemmte sich hinter die Sache und obsiegte im „Wettlauf um das Telefonpatent“ – trotz seiner windigen Apparaturen. Zu Recht ist heute Alexander Graham Bell als der Erfinder des Telefons bekannt. Übrigens ging es anderen ähnlich wie dem Elisha Gray: Sie hatten wie beispielsweise Johann Philipp Reis nicht den „richtigen Biss“.
Was zeichnet den Problemlösungsprozess aus? Gray und Bell haben rein zufällig die Lösung für ein Problem gefunden, das sie eigentlich gar nicht hatten. Und das ist der Witz vieler Erfindungen: Die Lösung ist da, bevor das Problem richtig verstanden worden ist. Meist mehrfach und an vielen Orten der Welt.
Die Erfindung aber macht der, der das Problem als erster sieht. Und das war im Falle des Telefons nun einmal Bell. Und darin liegt seine Genialität. Wer sich diesen Mechanismus des Erfindens einmal vor Augen hält, der wird auch die Leistung von Bill Gates besser würdigen können.
Ein nach Einfachheitsgrundsätzen aufgebauter Compiler führte zu einer unerwartet weiten Verbreitung der Programmiersprache Pascal. Niklaus Wirth kommentierte diesen überraschenden Nebeneffekt in seiner Turing Award Lecture so: „Even with the best intentions one may choose one’s goals wrongly.“
Bei der Erfindung des Buchdrucks scheint die Sache ähnlich zu liegen. Es sind weniger die grundlegenden Ideen, die von Gutenberg kommen. Sogar die Sache mit den beweglichen Lettern kannte man wohl schon. Aber Gutenberg hat gesehen, welche Probleme man damit lösen kann. Ihm ging es um eine Technik, mit der sich stets gleich schöne Schriftzeichen und Schriftbilder in einem Buch erzeugen lassen (Giesecke, 1998). Die Massenfertigung und Popularisierung von Büchern war ein ursprünglich gar nicht angestrebter Nebeneffekt, den Gutenberg dann aber doch konsequent nutzte.
Das ist das Wesen der Evolution allen Lebens: Die Variation des Erbmaterials, des Lösungswissens sozusagen, geschieht rein zufällig und alles andere als zielgerichtet. Erst wenn eine solche Variation von Vorteil ist, kann man sehen, welches Problem damit gelöst worden ist.
Irrtum 4: Wer Neues schaffen will, muss flexibel sein
Flexibilität ist ausgezeichnet, wenn es darum geht, die Ideen eines anderen umzusetzen. Eine prächtige Tugend des Mittelmaßes. Aber schauen wir uns die großen Erfinder und Entdecker an: Hier finden wir Hartnäckigkeit bis hin zur Sturheit. Sie halten – gegen alle Widrigkeiten – am einmal gefassten Vorhaben fest.
Musterbild eines solchen Sturkopfes ist Christoph Columbus: Durch keinen noch so gut begründeten Einwand ließ er sich von seiner Idee eines kurzen Seewegs nach Indien abbringen. Dabei ging er von einer Vorstellung aus, die den Erdumfang wesentlich unterschätzte und die in der damaligen wissenschaftlichen Welt bereits als gründlich widerlegt galt.
Konrad Zuse wurde nach seinem Studium Statiker bei den Henschel-Flugzeug-Werken. Im Jahr 1935 beschloss er, Computererfinder zu werden: „Ich war jung und wusste weit Besseres mit meiner Zeit anzufangen, als sie mit öden Rechnungen zu verbringen. Also sucht ich nach einer Lösung.“ (Fulda, 1992) Den ersten voll funktionsfähigen Computer hat Zuse 1941 fertig gestellt. Seine Lebenserinnerungen lassen die Unbeirrbarkeit erahnen, die hinter dieser Leistung steckt (Zuse, 1984).
Natürlich kann der große Geist mit seiner Sturheit auch einmal groß daneben liegen, wie etwa Albert Einstein mit seinen Angriffen auf die Quantentheorie. Aber letztlich haben sogar diese Angriffe Großes bewirkt: Die Widerlegung seiner Einwände führte zur Stärkung dieser Theorie (D’Espagnat, 1980).
Evolution kooperativen Verhaltens
|
Projektdokumentation: KoopEgo.pdf Java-Archiv: KoopEgo.jar Letzter Stand: 05.08.2009 |
Hinweise zur Arbeit mit dem Java-Archiv: Übertragen Sie das Archiv in ein lokales Verzeichnis Ihres Rechners und packen Sie es dort aus (mit WinZip oder dergleichen). Das Java-Archiv und die ausgepackten Dateien stehen also in demselben Verzeichnis. Starten sie das Programm durch Doppelklick auf die Archiv-Datei. Achtung: Die Projekte sind als Studienobjekte konzipiert und einem laufenden Verbesserungsprozess unterworfen. Letztgültige Informationen über die Parameterbelegung und die Formate der Eingabe erhalten Sie jeweils über den Hilfe-Knopf des Programms. |
Wie das Neue in die Welt kommt und warum Egoisten so freundlich sind
Das Java-Programm KoopEgo macht die Bedingungen sichtbar, unter denen in einer Welt aus Egoisten kooperatives Verhalten entstehen und sich behaupten kann. Die Welt in diesem Programm ist schachbrettartig strukturiert und jedes Wesen nimmt ein Feld dieser Welt ein. Die Farbe des Feldes spiegelt den Charakter des Wesens wieder. Jedes Wesen kann auf ein anderes aus seiner näheren Nachbarschaft treffen und sich – gemäß seinem Charakter – entscheiden, entweder mit dem anderen zu kooperieren oder ihn zu betrügen. Die Spielregeln und Auszahlungen folgen der Spielmatrix des Gefangenen-Dilemmas.


Das linke Bild zeigt, wie sich aus einem recht chaotischen Anfangszustand heraus nach einer Weile die Welt aufgrund der überall anzutreffenden Betrüger (grün und cyan) nahezu entvölkert hat (leere Plätze sind schwarz). Aber es sind auch schon erste Ansätze für Kolonien der Kooperation erkennbar (rot, magenta und blau). Der gutmütige Trottel (gelb) ist blind kooperativ und bei so viel Bosheit rundum auf der Verliererspur.
Etwas später hat sich das Bild gründlich geändert: Die Betrüger sind auf dem Rückzug. Restbestände sind nur noch in der Nähe gutmütiger Trottel zu finden. Übrig bleiben die freundlichen Strategen, die sich gegen Betrüger zu wehren wissen, beispielsweise Tit for Tat (rot), aber auch der konsequente Vergelter (magenta) und der Pawlow-Stratege (blau). Sogar einige gutmütige Trottel sind gerettet. Wir finden sie inmitten von wehrhaften, aber grundsätzlich freundlichen Strategen. Im Programm KoopEgo gibt es nicht nur die hier angesprochenen Grundstrategien. Über Eingabeparameter ist eine Vielzahl von Evolutionsbedingungen darstellbar.
Weiterführende Studien: Betrug und Vergeltung: Analyse und Experimente zur Lösung des Gefangenendilemmas
Rundfunkbeitrag: hr4 19.April.2007.mp3
Beitrag zum Darwin-Jahr 2009: Ist das Gute göttlich oder Ergebnis der Evolution? skeptiker (2009) 2, S. 60-67
Three Colour Maps
|
Projektdokumentation: ThreeColourMaps.pdf Java-Archiv: ThreeColourMaps.jar Letzter Stand: 02.09.2009 |
Hinweise zur Arbeit mit dem Java-Archiv: Übertragen Sie das Archiv in ein lokales Verzeichnis Ihres Rechners und packen Sie es dort aus (mit WinZip oder dergleichen). Das Java-Archiv und die ausgepackten Dateien stehen also in demselben Verzeichnis. Starten sie das Programm durch Doppelklick auf die Archiv-Datei. Achtung: Die Projekte sind als Studienobjekte konzipiert und einem laufenden Verbesserungsprozess unterworfen. Letztgültige Informationen über die Parameterbelegung und die Formate der Eingabe erhalten Sie jeweils über den Hilfe-Knopf des Programms. |
Das Programm soll zu einer vorgegebenen Landkarte bestimmen, ob und gegebenenfalls wie diese Karte mit drei (optional: vier) Farben koloriert werden kann, so dass je zwei aneinander angrenzende Länder verschiedene Farben haben. Diese Aufgabenstellung wird als Satisfiability-Problem formuliert und in ein Optimierungsproblem transformiert: Es werden Lösungen gesucht, die nur möglichst wenige der Färbungsbedingungen verletzen. Die Optimierung geschieht mit dem KoopEgo-Evolutionsverfahren, erweitert um Crossing-Over und simulierte Abkühlung (Simulated-Annealing).
Das Evolutionsverfahren: Die Felder der schachbrettartigen Welt sind mit Individuen besetzt, die je ein Färbungsmuster repräsentieren. Das Färbungsmuster ist sozusagen das Gen des Individuums. Und die Farbe Feldes, das das Individuum in der Welt selbst besetzt, gibt die Qualität des Färbungsmusters wieder: Gute Färbungsmuster, also solche, die nur wenige Bedingungen verletzen, werden blau dargestellt und schlechte bekommen eine rote Farbe. Mittlere Qualitäten erhalten entsprechende Zwischenfarben des Regenbogens.
Je Spielzug wird ein Platz der Welt rein zufällig als Zentrum bestimmt. Aus der Umgebung des Zentrums wiederum werden im Falle des Crossing-Over zwei Individuen gewählt. Das sind die Eltern eines neuen Individuums. Falls kein Crossing-Over stattfindet, wird nur ein Individuum als Elter ausgewählt. Da das Zentrum zur eigenen Umgebung gehört, kann auch das zentrale Individuum Elter sein. Das Gen (hier: Färbungsmuster) des neuen Individuums ist Ergebnis einer Crossing-Over-Operation, angewandt auf die Gene der Eltern oder, im Falle nur eines Elters, einer Klonung. Das Gen wird anschließend einer Mutationsoperation unterzogen. Liefert das so geschaffene neue Individuum einen besseren Färbungsvorschlag als das zentrale Individuum, so wird letzteres durch das neue Individuum ersetzt. Ansonsten wird das neue Individuum verworfen. Bei der simulierten Abkühlung hängt die Wahrscheinlichkeit für eine Ersetzung vom Grad der Verbesserung ab.
Der so definierte Spielzug ist der Kern des hier propagierten Evolutionsverfahrens. Der Spielzug konzentriert die Elternauswahl, die Nachwuchserzeugung und die Selektion auf das Wesentliche. Er ist leicht zu verstehen und ermöglicht so eine direkte Steuerung des Evolutionsprozesses durch den Anwender. Zur Philosophie dieses Evolutionsverfahrens gehört, dass der Anwender den Fortgang der Evolution durch ein Fenster zur simulierten Welt beobachten und die wesentlichen Steuerungsparameter interaktiv verändern kann. Diese Herangehensweise empfiehlt sich, denn die „Parameteroptimierung fällt in die Kategorie der schlecht definierten, schwach strukturierten (oder wenigstens kaum verstandenen) Probleme, die sich einer analytischen Behandlung entziehen” (Michalewicz, Fogel, 2000, S. 299).
Die folgende Bildschirmkopie zeigt eine Einfärbung der Landkarte der USA. Es sind vier Farben zugelassen. Die rechts gezeigte Welt repräsentiert 1600 Färbungsmuster. Das links dargestellte Färbungsmuster gehört zum roten Feld. Es ist das schlechteste der in der Welt gerade vorhandenen Färbungsmuster. Es verletzt 24 Bedingungen. (Das heißt: Es lassen sich 24 Paare einander angrenzender und gleich eingefärbter Länder finden.) Die besten Bewohner der Welt (blaue Felder) repräsentieren Färbungen, die nur fünf Bedingungen verletzen. Nach zwei Millionen Spielzügen mit einer Crossing-Over-Wahrscheinlichkeit von 50% und einer Mutationswahrscheinlichkeit von 10% wird eine perfekte Färbung gefunden.
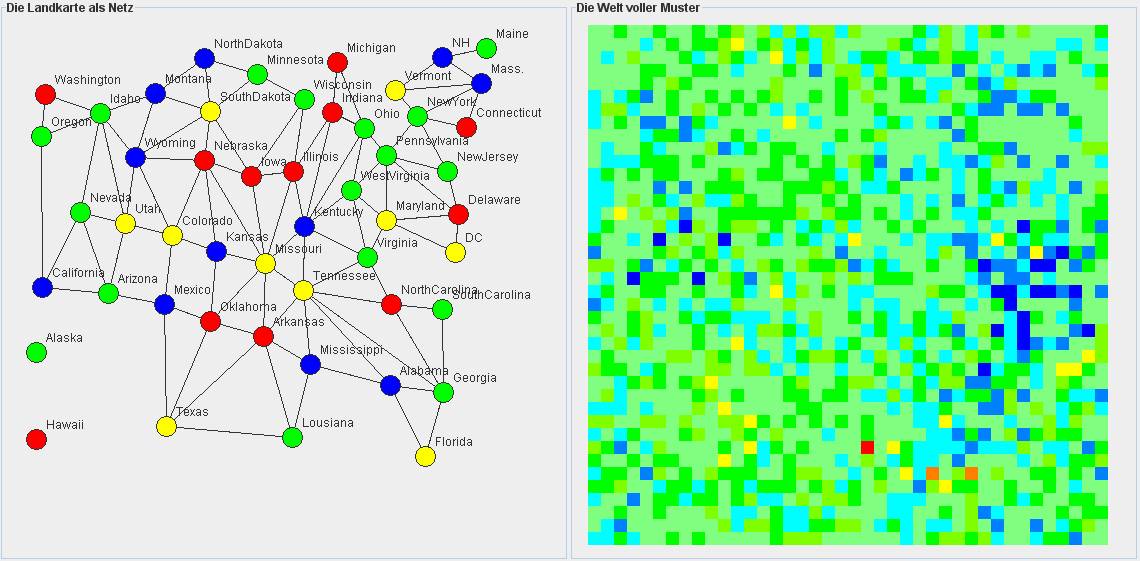
Das Evolutionsverfahren ist sehr allgemein gehalten und kann durch geeignete Parameterwahl beispielsweise auf ein reines Mutations-Selektions-Verfahren reduziert werden. Letzteres wird erreicht, indem man die Welt auf ein einziges Feld beschränkt und die Temperatur der simulierten Abkühlung auf null setzt. Das Crossing-Over spielt dann keine Rolle mehr und kann durch Setzen auf die Wahrscheinlichkeit null ausgeschaltet werden. Separat und parallel ablaufende Mutations-Selektions-Verfahren lassen sich dadurch realisieren, dass man in einer Welt mit vielen Feldern die Umgebung eines jeden Feldes auf dieses selbst beschränkt.
Rekonfigurierbare Fertigungszellen
|
Projektdokumentation: Java-Archiv: Letzter Stand: 05.08.2009 |
Hinweise zur Arbeit mit dem Java-Archiv: Übertragen Sie das Archiv in ein lokales Verzeichnis Ihres Rechners und packen Sie es dort aus (mit WinZip oder dergleichen). Das Java-Archiv und die ausgepackten Dateien stehen also in demselben Verzeichnis. Starten sie das Programm durch Doppelklick auf die Archiv-Datei. Achtung: Die Projekte sind als Studienobjekte konzipiert und einem laufenden Verbesserungsprozess unterworfen. Letztgültige Informationen über die Parameterbelegung und die Formate der Eingabe erhalten Sie jeweils über den Hilfe-Knopf des Programms. |
Bei diesem Projekt geht es um ein Thema der Fabrikplanung, speziell
um die Fließfertigung im Automobilbau mit festen Taktzeiten für die
einzelnen Arbeitsstationen.
In vielen Fällen läuft die Fertigungs- oder Maschinenbelegungsplanung darauf hinaus, eine Menge von Objekten in eine optimale zeitliche oder räumliche Reihenfolge zu bringen. Solche Objekte können Aufträge (Jobs) oder Arbeitsschritte (Tasks) sein. Die Objekte unterliegen Randbedingungen hinsichtlich der verfügbaren Ressourcen (Werkzeuge und Maschinen) und der Reihenfolge. Beispielsweise können zwei Teile erst dann miteinander verschweißt werden, wenn sie vorher zusammengeführt worden sind. Die Optimalität misst sich am Zeitbedarf sowie am materiellen und personellen Aufwand.
Bei der Planung rekonfigurierbarer Fertigungszellen müssen die anstehenden Arbeitsvorgänge wie Fördern, Spannen, Falzen, Schweißen und Kleben in eine optimale Reihenfolge gebracht werden. Dieser Arbeitsplan legt den Fertigungsablauf fest. Die Fertigungszelle hat einen Eingangs- und einen Ausgangsspeicher und eine Reihe von Fertigungsplätzen oder Stationen. Jede der Stationen besteht im Wesentlichen aus einem Roboter für Bearbeitung und Handhabung. Zwischen den Stationen gibt es Ablagen oder Transporteinrichtungen. Das folgende Bild gibt einen Eindruck vom Aufbau einer solchen Fertigungszelle wieder. Eingezeichnet ist außerdem der Weg eines Werkstücks.
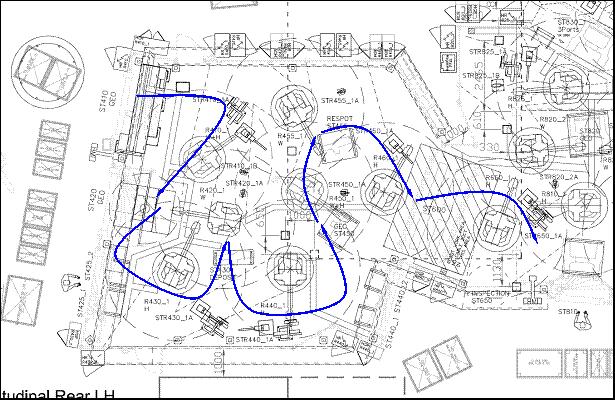
Das Werkstück durchläuft die Stationen in einer Reihenfolge, die durch den Arbeitsplan bestimmt ist. Jede Station arbeitet einen zusammenhängenden Abschnitt des Arbeitsplans innerhalb einer vorgegebenen Taktzeit von beispielsweise 70 Sekunden ab. Danach wird das Werkstück an die nächste Station weitergegeben, die den folgenden Arbeitsplanabschnitt erledigt.
Das Musterproblem aus dem Problemkreis der Planung von Reihenfolgen ist das Handlungsreisenden-Problem (Traveling Salesman Problem). Generationen von Unternehmensforschern haben sich die Zähne daran ausgebissen, denn es handelt sich um ein schweres Problem. Es ist schwer in dem Sinn, dass der Aufwand für das Finden einer optimalen Lösung mit der Anzahl n der anzuordnenden Objekte gewaltig steigt. Präzise: Der Aufwand – die Zahl der Iterationsschritte – lässt sich nicht durch A∙nk begrenzen, egal wie groß man die Werte A und k auch wählt.
Ein nahe liegender Algorithmus zum Auffinden der optimalen Anordnung ist das Ausprobieren aller n! möglichen Anordnungen. Das ist die Methode der vollständigen Enumeration. Bereits bei einer mäßig großen Anzahl von Objekten ist sie praktisch unmöglich durchführbar. Für n=170 lässt sich die Anzahl der möglichen Anordnungen, die Zahl der Permutationen, gerade noch mit dem Double-Format darstellen. Es handelt sich um eine 307-stellige Dezimalzahl, eine unvorstellbare Größe. Könnte ein Computer eine Milliarde Anordnungen je Sekunde prüfen, hätte er nach zwanzig Milliarden Jahren erst einen verschwindend kleinen Teil der Arbeit erledigt, darstellbar als 27-stellige Dezimalzahl.
Die Suche nach Verfahren, die den Aufwand für die Optimumsuche auf ein erträgliches Maß reduzieren, hat bisher nichts Ermutigendes zu Tage gefördert. Evolutionsverfahren versprechen zwar nicht das Optimum, aber man kann damit gute Lösungen in überschaubarer Zeit finden.
Die Optimierung geschieht in diesem Projekt wieder mit dem KoopEgo-Evolutionsverfahren, erweitert um Crossing-Over und simulierte Abkühlung (Simulated-Annealing). Ein Beispiel: 88 Arbeitsvorgänge sind zu bearbeiten. Eine Aufteilung der vorsortierten Folge dieser Arbeitsvorgänge erfordert 40 Arbeitsstationen (Roboter). Durch die Optimierung der Reihenfolge kann die Zahl der erforderlichen Arbeitsstationen auf 35 gesenkt werden.
Fahrweisenoptimierung
|
Projektdokumentation: FahrweisenOptimierung.pdf Java-Archiv: FahrweisenOptimierung.jar Letzter Stand: 05.08.2009 |
Hinweise zur Arbeit mit dem Java-Archiv: Übertragen Sie das Archiv in ein lokales Verzeichnis Ihres Rechners und packen Sie es dort aus (mit WinZip oder dergleichen). Das Java-Archiv und die ausgepackten Dateien stehen also in demselben Verzeichnis. Starten sie das Programm durch Doppelklick auf die Archiv-Datei. Achtung: Die Projekte sind als Studienobjekte konzipiert und einem laufenden Verbesserungsprozess unterworfen. Letztgültige Informationen über die Parameterbelegung und die Formate der Eingabe erhalten Sie jeweils über den Hilfe-Knopf des Programms. |
Das Programm soll für einen Eisenbahnzug die optimale Fahrweise bestimmen. Der Zug (beispielsweise ein ICE 1 mit 12 Mittelwagen) soll eine vorgegebene gerade Strecke in möglichst kurzer Zeit und mit möglichst geringem Energieverbrauch zurücklegen. Dabei sind abschnittsweise gegebene Geschwindigkeitsbeschränkungen einzuhalten. Die Fahrt sollte mit möglichst wenigen Fahrstufenumschaltungen auskommen. Die Optimierung geschieht in diesem Projekt mit dem KoopEgo-Evolutionsverfahren, erweitert um Crossing-Over und simulierte Abkühlung (Simulated-Annealing).
Jedes Individuum der Welt repräsentiert eine komplette Fahrt. Sie setzt sich aus Teilstrecken mit jeweils konstanter Fahrstufe zusammen. Optimierungsziel ist eine möglichst günstige Aufteilung der Gesamtstrecke in Teilstrecken und die Wahl der passenden Fahrstufen.
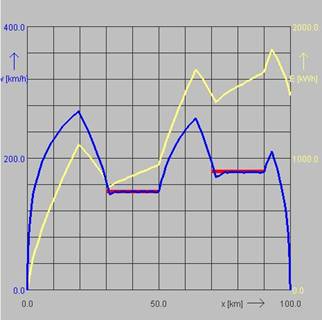
Wir wählen als Beispiel eine Strecke der Länge 100 km. Von Kilometer 30 bis 50 besteht eine Geschwindigkeitsbeschränkung auf 150 km/h. Von Kilometer 70 bis 90 ist die Geschwindigkeitsbeschränkung gleich 180 km/h. Optimierungsziele sind eine möglichst kurze Fahrzeit und eine geringe Zahl von Fahrstufenwechseln. Energiesparsame Fahrweise ist nicht gefordert. Erwartet wird ein straffe bzw. spitze Fahrweise, bei der der Zug durchgehend – abgesehen von wirksamen Geschwindigkeitsbeschränkungen – mit maximaler Zugkraft beschleunigt bzw. mit. maximaler Betriebsbremskraft abbremst. Diese Prognose wird durch das Simulationsergebnis bestätigt (Bild unten links). In der Grafik ist die Geschwindigkeit in Abhängigkeit vom Weg blau eingetragen, der Energieverbrauch gelb. Abfallende Energiekurven gehen auf die Energierückspeisung beim betrieblichen Bremsen zurück.
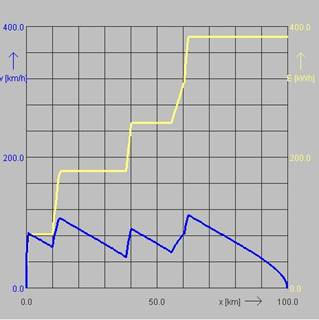
In einem weiteren Experiment wird wieder eine Strecke der Länge 100 km gewählt. Diesmal ist sie frei von Geschwindigkeitsbeschränkungen. Ziele sind eine möglichst kurze Fahrzeit, eine geringe Zahl von Fahrstufenwechseln und energiesparsame Fahrweise. Da das Fahren mit fest eingestellter Geschwindigkeit (Cruisen) nicht zu den Optionen der Fahrtauswahl gehört, kommt es hier zu Lösungen mit Ausrollen (Coasten). Das ergibt sägezahnartige Geschwindigkeitsdiagramme. Ein typisches Ergebnis ist im Bild unten rechts zu sehen.
Literaturhinweise
Ayala, Francisco J.: Mechanismen der Evolution. Spektrum der Wissenschaft (1979) 5, 8-18
Boltzmann, L.: Populäre Schriften. Ausgewählt von Engelbert Broda. Vieweg, Braunschweig 1979
Böszörményi, László; Gutknecht, Jürg;
Pomberger, Gustav: The School of Niklaus Wirth. „The Art of Simplicity“. dpunkt.verlag,
Academic Press, Heidelberg 2000
Carroll, Sean, B.: Evo Devo. Das neue Bild der Evolution. Berlin University Press 2008
Dawkins, Richard: Das egoistische Gen. Springer-Verlag, Berlin, Heidelberg 1978
D’Espagnat, Bernard: Quantentheorie und Realität. Spektrum der Wissenschaft (1980) 1, 68-81
Giesecke, Michael: Gutenberg, die neuen Medien und die Zukunft der Informationsgesellschaft. Spektrum der Wissenschaft (1998) 11, 148-153).
Holland, John H.: Genetische Algorithmen. Spektrum der Wissenschaft (1992) 9, 44-51
Hounshell, David A.: Der Wettlauf um das Telefon-Patent. Spektrum der Wissenschaft (1981) 3, 106-114
Michalewicz, Zbigniew; Fogel, David B.:
How to Solve It: Modern Heuristics. Springer-Verlag, Berlin, Heidelberg 2000
Michalewicz, Zbigniew; Michalewicz, Matthew: Puzzle-based Learning: An introduction to critical thinking, mathematics, and problem solving. 2008
Monod, Jacques: Zufall und Notwendigkeit. Philosophische Fragen der modernen Biologie. Piper, München, Zürich 1971
Nüsslein-Volhard, Christiane: Das Werden des Lebens. Wie Gene die Entwicklung steuern. C.H.Beck, München 2004
Rechenberg, Ingo: Evolutionsstrategie. Optimierung technischer System nach den Prinzipien der biologischen Evolution. Friedrich Frommann Verlag, Stuttgart-Bad Cannstatt 1973
Stebbins, G. Ledyard; Ayala, Francisco J.: Die Evolution des Darwinismus. Spektrum der Wissenschaft (1985) 9, 58-71
Zuse, Konrad: Der Computer – Mein Lebenswerk. Springer-Verlag, Berlin, Heidelberg 1984, 1990
© Timm Grams, 21. August 2009 (zuletzt aktualisiert am 12.11.09)
