Klug entscheiden bei Risiko |
|
ÜbersichtWir entscheiden Dinge häufig aus dem Bauch heraus und bereuen dann, nicht besser überlegt zu haben. Der Hypertext will helfen, zu klügeren Entscheidungen zu kommen. Er beginnt mit einer
Meine Veröffentlichungen zum Thema "menschliches Versagen" und Bedienfehler stellen die Notwendigkeit einer normativen Modellierung des Verhaltens von Piloten, Fahrern, Operateuren - kurz: Bedienern - heraus. Das kommentierte Literaturverzeichnis ist Quellennachweis und es bietet Anreize und Hinweise für das weitere Studium. Ergänzendes Material bietet die Sammlung der Denkfallen und Paradoxa. Hin und wieder werden Fehlentscheidungen auf Denkfallen zurückgeführt. In diesen Fällen wird auf das System der Denkfallen verwiesen. |
Entstehung der BegriffeAnfangs war alles SchicksalAllein Exaktheit geht von den Göttern der Griechen aus. Die Griechen haben kein Interesse an Experimenten und Naturgesetzen. Beweise zählen, sonst nichts. Das Leben ist unabänderliches Schicksal. Odysseus ist ein Held ohne Bewusstsein. Das Konzept des Willens ist eine späte Schöpfung des griechischen Denkens. Dann kam das KalkülIn der Renaissance entsteht der Wunsch, die Zukunft zu kontrollieren. Die Begriffe Wahrscheinlichkeit und Risiko erhalten ihr mathematisches Fundament. Nutzen und Risiken von Handlungsalternativen werden objektiviert. Sie lassen sich durch Zahlen erfassen und miteinander vergleichen. In Lloyd's Coffee House (eröffnet 1687) werden Risiken zur Handelsware. Das Versicherungswesen expandiert. Rationale Entscheidungen sind subjektivDer Begriff des objektiven Risikos ist als Basis für rationale Entscheidungen noch zu schwach. Er berücksichtigt nicht die betroffenen Personen und deren unterschiedlichen Einstellungen zum Risiko. Daniel Bernoulli ergänzt den Risikobegriff um die subjektive Komponente. Er führt die Nutzenfunktion ein. Sie trägt der Risikoaversion oder der Risikoakzeptanz eines Entscheiders und Risikoträgers Rechnung. Damit ist die Grundlage für ein normatives Modell der rationalen Entscheidung gelegt. Als bittere Erkenntnis bleibt, dass rationale Entscheidungen nicht objektivierbar sind. Widersprüche bleibenDie empirische Forschung belegt, dass es viele systematische Abweichungen von der Norm rationalen Verhaltens gibt. Eine lohnende Gegenstrategie ist das Studium der Merkmale von Situationen, in denen es zu Fehlentscheidungen kommt - das Aufdecken und systematische Erfassen von Denkfallen und fehlleitenden Heuristiken. Entscheidungsfindung ist zum Großteil Stückwerkstechnik. Bausteine dieser Stückwerkstechnik bieten die wegweisenden Arbeiten von Kahneman und Tversky. Fragwürdige Grundlagen der Moral"Was du nicht willst, das man dir tu', das füg auch keinem andern zu" ist angesichts der Subjektivität aller Risikowahrnehmung keine hilfreiche Verhaltensmaxime mehr. Mit der Goldenen Regel verlieren wir den letzten Rest an festem Grund. "Die Unsicherheit des reflektierenden Menschen ist zwangsläufig total" (Felix von Cube). |
Fehlentscheidungen - eine Fallsammlung
Fall 1: Ein Arbeitskollege erzählt, dass er jetzt nicht mehr in der Stadt, sondern mitten im Odenwald wohnt. Das Haus sei erschwinglich, die Luft rein, es gäbe viel Natur rundherum, man könne sich wohl fühlen. Ein Jahr später treffe ich ihn wieder. Ein erneuter Umzug steht an - zurück in die Stadt. Er meint: "Wir haben viele Freunde und freuen uns über jeden Besuch. Seit wir im Odenwald wohnen, fahren die nur noch an uns vorbei. Die Einsamkeit nervt."
Fall 2: Folgendes trug sich im Ärmelkanal zu: "Ein Frachter wollte Zeit sparen, fuhr einen falschen Fahrweg und kollidierte mit einem Öltanker, der explodierte, so dass noch 10 km entfernt in Folkestone Fensterscheiben zu Bruch gingen. Auch der Frachter ging auf Grund, aber da der Kanal ein relativ seichtes Gewässer ist, stellte er für die anderen Schiffe ein gefährliches Hindernis dar und wurde deshalb mit Warnbojen markiert [und nach weiteren Zwischenfällen durch zwei Feuerschiffe gesichert] ... Zwei Wochen später ignorierte ein Tanker unbekannter Identität eine Sperre aus Leuchtraketen und Blinklichtern der beiden Feuerschiffe, durchpflügte eine Reihe von Leuchtbojen und schaffte es zur Überraschung aller, unbeschädigt durchzukommen und in der Nacht zu verschwinden ... Mittlerweile waren an dieser Stelle 47 Menschen ums Leben gekommen. Nach Berichten der englischen Küstenbehörden hatten innerhalb von zwei Monaten 16 Schiffe die Warnzeichen ignoriert und ihren Weg durch das Unfallgebiet genommen - es war die schnellste Route" (Perrow, 1999).
Fall 3: Programmierpraktikum. Eine Gruppe stellt ihr Programm vor. Mir fällt auf, dass für eine Teilaufgabe nicht eine bereits früher gefundene gute Lösung übernommen worden ist, sondern eine schwächere. Ich frage: "Warum diese Variante?" - "Mit der anderen hat das Programm nicht funktioniert." - "Wie nicht funktioniert?" - "Nach dem Start gab es keinerlei Reaktion mehr. Der Computer musste neu gestartet werden." Ich bitte, das Programm neu zu übersetzen. Der Übersetzer liefert eine Flut von Warnungen. Aber er schließt die Übersetzung erfolgreich ab. "Solche Warnungen kommen öfter - auch bei anderen Programmen. Sie sind harmlos." Ich sage: "Wir akzeptieren keine Warnungen." Das Programm wird Schritt für Schritt verbessert. Die Warnungen verschwinden nach und nach. Übrig bleibt eine Warnung, die sich auf einen Programmierfehler mit schwer überschaubaren Auswirkungen zurückführen lässt. Der hat aber überhaupt nichts mit dem Teilprogramm zu tun. Nach Beseitigung des Fehlers läuft auch die ursprüngliche Variante einwandfrei.
Rezepte für kluge Entscheidungen
Bevor es an das Entscheiden geht, muss der Entscheider sich seine Entscheidungssituation vollkommen klar machen. Viele Fehlentscheidungen fallen, weil eben nicht klar ist, um was es geht, welche Ziele verfolgt werden und was die Konsequenzen des Tuns sind. Die Sammlung von Fehlentscheidungen enthält genug Beispiele für schlecht definierte und wenig verstandene Problemlagen. Wenn Sie meinen, vor einer wichtigen Entscheidung zu stehen, beantworten Sie die folgenden fünf Fragen, die Hammond, Keeney und Raiffa den Lesern des Buches Smart Choices vorlegen.
1. Was ist das Problem?
Machen Sie sich klar, was genau zu entscheiden ist. Das Ergebnis wird stark vom Blickwinkel beeinflusst. Übernehmen Sie nicht stillschweigend und ungeprüft irgendwelche Voraussetzungen. Stellen Sie Ihre Vorurteile in Frage. Meiden Sie Blickverengung und voreilige Hypothesenbildung. Versuchen Sie, das Problem zu verallgemeinern. Wollen Sie wirklich nur mehr Natur um sich herum oder geht es ihnen darum, das Wohnumfeld zu verbessern, ohne dabei ein anderes ihrer Bedürfnisse zu vernachlässigen?
2. Sind die Absichten wirklich klar?
Mit ihrer Entscheidung wollen Sie ja irgend etwas erreichen. Stellen Sie fest, welche Interessen, Werte, Besorgnisse, Ängste oder Wünsche besonders relevant für die Erreichung ihres Zieles sind.
3. Welche Alternativen bieten sich?
Wieder steht die Überwindung der Blickverengung im Vordergrund. Wenn Sie mögliche Handlungsalternativen unbedacht lassen oder leichthin von vornherein ausschließen, besteht die Gefahr, dass sie ungewollt gerade die beste Alternative unberücksichtigt lassen. Die Programmierer (Fall 3 der Fallsammlung) haben entschieden, es mit einem anderen Programmstück zu versuchen. Die Alternative, erst einmal eine genaue Fehleranalyse durchzuführen, haben sie verworfen. Das war verkehrt.
4. Was sind die Konsequenzen?
Haben Sie die Konsequenzen jeder Alternative gut genug durchdacht? Alternativen können verlockend sein und uns täuschen.
|
Tabelle der Konsequenzen |
|||
|
Ziele und Absichten |
Alternativen (Wohnungen) |
||
|
Odenwald |
Stadtrand |
Vorort |
|
|
Entfernungen (Arbeit, Schule, Einkauf) |
groß |
gering |
mittel |
|
Qualität der Schule |
mittel |
mittel |
gut |
|
soziale Kontakte |
gering |
gut |
gut |
|
Kosten |
gering |
mittel |
mittel |
Vielleicht hätte der Kollege aus Fall 1 sich eine Tabelle der Konsequenzen aller ihm offenstehenden Alternativen, gemessen an seinen Zielen und Absichten, angelegen sollen. Eine grobe und verkürzte Version dieser Tabelle ist rechts zu sehen.
Dann wäre ihm wohl rechtzeitig gekommen , dass die vielbeschäftigten Freunde, die auf einer der Autobahnen der Rheinebene hin und wieder vorbeikommen, wohl eher einen Zwischenstopp in der Großstadt als mitten im Odenwald einlegen. Das ländliche Leben wäre dann wohl weniger verlockend erschienen.
Wie schwer wir uns zuweilen damit tun, die Konsequenzen von Entscheidungen zu durchdenken, führt uns das Braess'sche Paradoxon vor Augen.
5. Was ist wichtig, was weniger?
Absichten und Ziele laufen einander oft zuwider. Beispielsweise lassen sich ruhige Wohnumgebung und vielfältige soziale Kontakte nur schwer miteinander vereinbaren. In solchen Fällen heißt es abwägen. Was ist mir wichtiger: die Ruhe oder die Anregung? Es empfiehlt sich, Prioritäten zu setzen, um die konkurrierenden Absichten in ein bekömmliches Gleichgewicht zu bringen. Es gibt sehr einfache und wirkungsvolle Methoden für die Herstellung einer Rangordnung der Alternativen:
- Zunächst kann man für jedes der Ziele eine separate Rangordnung der Alternativen einführen und Bewertungszahlen zuordnen.
- Dann streicht man die Alternativen, die in der Rangfolge bezüglich mehrerer wichtiger Ziele hinten liegen.
- Das paarweise Vergleichen von Alternativen erlaubt je Vergleichsvorgang die Konzentration auf die wenigen Ziele, in denen sich die jeweiligen Alternativen wesentlich unterscheiden. Da es nur um die beste Alternative geht, kann das K.-o.-Prinzip die Arbeit erleichtern: Ist eine Alternative einmal Verlierer im direkten Vergleich mit einer anderen, wird sie nicht weiter berücksichtigt.
- Eine weitere Möglichkeit ist es, für jede der Alternativen eine Gesamtpunktzahl zu ermitteln, die sich als Summe von (je nach Bedeutung eines Zieles) gewichteten Bewertungszahlen ergibt. Über die Rangfolge der Alternativen entscheiden deren Gesamtpunktzahlen.
Oft sieht man schon nach gründlicher Beantwortung der fünf Fragen die richtige Entscheidung. Für kompliziertere Problemlagen müssen leistungsfähigere - aber auch anspruchsvollere - Methoden her, beispielsweise die Risikoanalyse. Sie ist Gegenstand des folgenden Abschnitts.
Risiken quantifizieren und vergleichen
In seiner Diplomarbeit beschreibt Oliver Geisen folgende Situation: Der Rechner ist defekt. Vermutlich ist entweder die Festplatte oder die Speichererweiterung kaputt. Zwei Möglichkeiten stehen offen: Kauf einer neuen Festplatte oder Kauf einer neuen Speichererweiterung. Beide Reparaturversuche können daneben liegen und dazu führen, dass schließlich beide Teile gekauft werden müssen. Nach etwas Überlegung ("Welche Alternativen bieten sich?") taucht als dritte Möglichkeit auf, den Rechner zur Reparatur in einen vertrauenswürdigen Computerladen zu bringen. Diese Dienstleistung kostet zwar extra. Dafür beinhaltet sie eine Diagnose und die Reparatur beschränkt sich auf das absolut Notwendige.
Eine qualitative Abwägung der Konsequenzen der drei Alternativen bringt wenig: Sie lassen sich nicht in eine Rangordnung bringen (Was ist wichtig, was weniger?). Wir brauchen Zahlenwerte, am besten die Kosten einer jeden der Alternativen. Aber: Wir wissen ja gar nicht, ob die Festplatte oder ob die Speichererweiterung defekt ist. Also können wir auch nicht von vornherein sagen, welche Kosten schließlich auflaufen. Aber über die Wahrscheinlichkeiten lässt sich doch sicher etwas in Erfahrung bringen.
Also wird im Computerladen angerufen. Ein Studienkollege, der dort manchmal aushilft, ist am Telefon und gibt bereitwillig Auskunft. Er meint, dass er nahezu gleich häufig Festplatte und Speichererweiterung austauschen muss. Etwas häufiger - in etwa 60% der Fälle - sind es die Festplatten. Eine neue Festplatte kostet 200 Euro und ein neues Speichermodul 100 Euro. Für die Arbeit berechnet der Computerladen pauschal 50 Euro.
Jetzt schauen wir uns die erste der Alternativen - Kauf einer Festplatte -
genauer an. In 60% der Fälle ist dann die Sache für einen Preis von 200 Euro
abgetan. In 40% der Fälle sind 300 Euro zu bezahlen. Den Erwartungswert der
Kosten nennen wir das objektive Risiko der gewählten Alternative. Es
beträgt 60%·200 + 40%·300 Euro, also 240 Euro.
|
Alternative |
Risiko |
|
Festplatte kaufen |
240 |
|
Speichererweiterung kaufen |
220 |
|
Reparatur im Laden |
210 |
Ähnlich verfahren wir in den anderen beiden Fällen. Die Ergebnisse sind in nebenstehender Tabelle zusammengefaßt. Jetzt lässt sich in die Alternativen eine Rangordnung bringen. Das objektive Risiko spricht für die Reparatur im Computerladen. An zweiter Stelle käme die Speichererweiterung. Vom objektiven Risiko her am ungünstigsten stellt sich der Kauf einer Festplatte dar. Es scheint vernünftig zu sein, die Reparatur dem Computerladen zu überlassen.
Natürlich hätte der Kauf der Speichererweiterung ein Treffer sein können. Dann wäre man mit ganzen 100 Euro davongekommen. Aber das ist eben nicht sicher. Wenn man nach dem geringsten objektiven Risiko entscheidet, wird man auf Dauer am besten fahren. Jedenfalls dann, wenn es sich um überschaubare Geldbeträge und um alltägliche Kaufentscheidungen handelt. Dann werden sich mit der Zeit die ungünstigen und die günstigen Ergebnisse ausgleichen, und man zahlt auf lange Sicht gesehen tatsächlich am wenigsten.
Die Analyse komplizierter Entscheidungssituationen führt man am besten auf der Grundlage eines Entscheidungs-Ereignisbaums durch.
In der Praxis trifft das Errechnen von Risiken auf Hindernisse. Eine Schwierigkeit liegt darin, dass oft Größen mit unterschiedlichen Maßeinheiten und Skalen miteinander zu verrechnen sind. Eine andere betrifft unsere schwachen Fähigkeiten im Umgang mit Wahrscheinlichkeiten. Allzuoft liegen unsere Schätzungen daneben, wie das Drei-Türen-Problem, die Harvard-Medical-School-Studie und die Halbkreis-Aufgabe zeigen.
Rationale Entscheidungen müssen nicht objektiv sein
Jubiläum im Kasino
Ein Spielkasino bietet jedem Besucher die einmalige Chance, für einen Einsatz von 1000 Euro an einem Spiel teilzunehmen. Die Regeln des Spiels sind einfach: Hat der Spieler seinen Einsatz entrichtet, wird ein Würfel geworfen. Zeigt dieser eine Sechs, erhält der betreffende Spieler seinen Einsatz zurück und 6000 Euro oben drauf. Andernfalls hat er den Einsatz verloren.
Jedem Besucher sind rasch die Gewinnaussichten klar: Mit der Wahrscheinlichkeit von 1/6 sind 6000 Euro zu gewinnen und mit der Wahrscheinlichkeit 5/6 sind 1000 Euro verloren. Könnte man dieses Spiel beliebig oft wiederholen, ergäbe sich ein mittlerer Gewinn von etwa 167 Euro je Spiel. Für das Spielkasino ist das ein schlechtes Geschäft.
Was für das Spielkasino schlecht ist, müsste für die Besucher gut sein - aber sonderbar: Nur wenige der Besucher nehmen das Angebot an. Was wäre passiert, wenn die Bank einen Einsatz von nur 10 Euro verlangt und den Gewinn im selben Verhältnis reduziert hätte? Vermutlich hätten sehr viel mehr Besucher das Angebot angenommen. Dabei wäre das Spiel im Prinzip gleich geblieben. Die im Mittel zu erwartende Auszahlung je Spiel überstiege auch dann den Einsatz um fast 17 Prozent. Wie lässt sich dieses sonderbare Verhalten der Besucher erklären?
Anmerkung zum Maßstab und zur Terminologie: Bisher haben wir von Schäden, Kosten und Risiken gesprochen. Jetzt geht es um Gewinne. Man sollte sich vorab auf den Maßstab und eine bestimmte Sprechweise festlegen. In der "Nutzenterminologie" gibt es nur Gewinne. Der Einsatz ist dann ein Gewinn mit negativem Vorzeichen. Rein mathematisch gesehen kann man auf alle Ergebnisgrößen den Einsatz aufaddieren. Dadurch wird objektiv gesehen die Entscheidungssituation nicht geändert. Aber die unschönen negativen Zahlen sind weg. In der "Nutzenterminologie" gewinnt der Spielbankbesucher, der am Spiel nicht teilnimmt, 1000 Euro. Der Mitspieler erhält, falls er gewinnt, 7000 Euro. Genausogut kann man die "Schadensterminologie" zugrunde legen: Bei Teilnahme am Spiel entsteht ein Verlust in Höhe des Einsatzes und im Falle der Nichtteilnahme einer in Höhe des möglichen Gewinns. In der Betriebswirtschaft herrscht die "Nutzenterminologie" vor, in der Technik die "Schadensterminologie".
Risiko ist subjektiv
|
|
Die meisten Menschen haben irgendwelche Wünsche - manches steht weit oben auf der Wunschliste, anderes eher unten. Es hängt von den persönlichen Lebensumständen und vom Wertesystem jedes Einzelnen ab, welches Hochgefühl die Erfüllung eines Wunsches bewirkt.
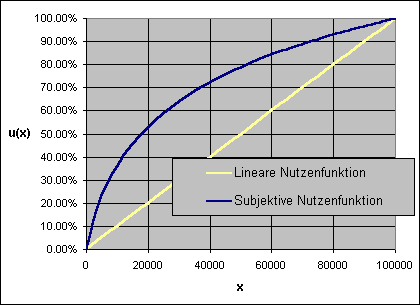
Horst Hemmerling hat für sich und seine Familie versuchsweise eine Rangordnung der Wünsche erstellt. Ganz oben steht der Erwerb einer Eigentumswohnung. Für hunderttausend Euro wäre dieser Wunsch erfüllbar. Horst misst den hunderttausend Euro einen subjektiven Nutzen von 100 % zu: hundertprozentiges Hochgefühl bei einem Lottogewinn von hunderttausend Euro. Aber auch die Hälfte davon wäre nicht übel. Nach Rücksprache mit der Familie stellt er fest: Die Eigentumswohnung wäre auch bei einem Gewinn von fünfzigtausend Euro noch erschwinglich. Durch den Schuldendienst müssten andere, weniger dringliche Wünsche zurückgestellt werden. Er kommt zur Überzeugung, dass das Hochgefühl nicht etwa mit nur 50 %, sondern mit etwa 80 % zu veranschlagen wäre. Ähnliche Verhältnisse wären bei einer weiteren Halbierung zu erwarten: Mit einem Gewinn von 25000 Euro läge - verglichen mit dem vollen Gewinn von 100000 Euro - sein Hochgefühl immer noch deutlich über 50 %. Horst ist Mathematiker und er findet nach einigem Hin- und Her eine Funktion, die sein Hochgefühl in Abhängigkeit vom Betrag wiedergibt. Er findet sogar eine recht einfache Formel für seine subjektive Nutzenfunktion (siehe Grafik).
Horst Hemmerling ist nicht gerade ein typischer Spielbankbesucher. Dennoch kommt er zum Jubiläum in das oben erwähnte Spielkasino. Er erfährt vom "vorteilhaften" Gewinnspiel und fragt sich: Warum sagt mir der Verstand, dass ich mitmachen soll und mein Gefühl ist dagegen? Das hat wohl etwas mit meiner subjektiven Nutzenfunktion zu tun. Vielleicht lässt sich damit meine Entscheidung sogar rational begründen? Also: Wenn ich nicht teilnehme, "gewinne" ich 1000 Euro, das ist der eingesparte Einsatz. Nehme ich teil, bekomme ich 7000 Euro mit einer Wahrscheinlichkeit von 1/6 oder gar nichts. Nun sagt mir meine persönliche Nutzenfunktion, dass 1000 Euro auf meiner Skala einen Nutzen von 6 % und 7000 Euro einen von ca. 30 % haben. Letzterer kommt nur mit einer Wahrscheinlichkeit von 1/6 zustande, so dass für mich der subjektive Nutzen des Spiels bei nur 5 % liegt. Das ist weniger als die 6 % bei Nichtteilnahme. Horst Hemmerling kommt zum Schluss, dass seine Entscheidung, das "vorteilhafte" Angebot nicht anzunehmen, sehr vernünftig ist!
Eine Formel für die subjektiven Nutzenfunktion
Horsts Überlegungen zur Nutzenfunktion im Detail: "Mein Hochgefühl hängt womöglich logarithmisch vom gewonnenen Betrag x ab. Bereits im 18. Jahrhundert hat ja Daniel Bernoulli einen solchen Ansatz gemacht. Die Funktion meines Hochgefühls lässt sich demnach mit irgendwelchen Konstanten c und x0 in der Form u(x) = c ln(x/x0) ausdrücken. Der Wert u(x) stellt für mich den subjektiven Nutzen des Betrags x dar. Das gilt zumindest für Beträge über 10000 Euro. Bei kleinen Beträgen bin ich mir nicht so sicher: Zwei Euro sind mir doch tatsächlich doppelt soviel wert wie ein Euro. Also korrigiere ich die Formel, so dass für Beträge über 10000 Euro näherungsweise das logarithmische und für Beträge unter 1000 Euro näherungsweise das lineare Nutzengesetz gilt. Mit dem Ansatz u(x) = c ln(1+x/x0) kann ich meine Empfindungen recht genau wiedergeben. Es handelt sich um eine konkave Funktion, also um eine Funktion, deren Steigung mit wachsendem x abnimmt. Der Ankerwert x0 muss in der Übergangszone zwischen den Gültigkeitsbereichen des linearen und des logarithmischen Nutzengesetzes liegen. Ein plausibler Wert ist 5000 Euro."
Das Sicherheitsäquivalent
Der Spielkasinobesucher steht vor einer Entscheidungssituation. Eine solche ist gekennzeichnet durch mehrere Entscheidungsalternativen. Im Fall des Würfelspiels sind es zwei: teilnehmen oder eben nicht. Jede solche Alternative ist mit einem gewissen subjektiven Nutzen verbunden. Da der Nutzen ein Zufallsergebnis sein kann, wird als Maß der Erwartungswert genommen, der subjektive Nutzenerwartungswert.
Für sich genommen sagt diese Größe allerdings wenig aus. Bei der Wahl der Nutzenfunktion kam es ja weniger auf die absoluten Werte als auf den Vergleich der Nutzenwerte verschiedener Alternativen an. Um zu einer anschaulichen Kennzahl für jede der Alternativen zu kommen fragen wir danach, welche sichere Auszahlung wohl denselben subjektiven Nutzen bietet wie die zufällige. Diese Auszahlung heißt Sicherheitsäquivalent.
Beispiel: Das Würfelspiel im Kasino hat für Horst Hemmerling einen subjektiven Nutzen von etwa 5%. Er ermittelt nun, welcher Geldbetrag für ihn genau diesen Nutzen hat. Er kommt auf ungefähr 800 Euro. Das Sicherheitsäquivalent des Spiels beträgt also circa 800 Euro (eine genauere Berechnung ergibt 785 Euro). Jetzt ist ganz klar: Der Einsatz von 1000 Euro wird durch die Gewinnaussicht nicht aufgewogen.
Risikoakzeptanz und Risikoaversion
Gleichzeitig risikoscheu und risikofreudig
Von risikoaversen Personen wird ein probabilistischer (also zufallsbestimmter) Nutzen tendenziell unterschätzt. Das heißt: das Sicherheitsäquivalent wird beim Übergang von einer linearen Nutzenfunktion zu einer konkaven zu niedrigeren Werten hin verschoben. Bei einem deterministischen Nutzen - einer fest vereinbarte Auszahlung zum Beispiel - gibt es diese Verschiebung nicht. Der risikoaverse Spieler hat demnach eine Tendenz zur Überbewertung der Gewissheit.
Diese Aussagen lassen sich mit dem Arbeitsblatt Utility.xls auf einfache Weise demonstrieren: Nehmen sie irgend eine zufällige Nutzenverteilung - beispielsweise die voreingestellte - und variieren Sie die Nutzenfunktion, indem Sie einmal den Ankerwert auf eine Million (nahezu lineare Nutzenfunktion) und ein andermal auf 5000 setzen. Dann führen Sie das Experiment mit einem deterministischen Nutzen durch. Dazu setzen Sie für irgendeinen x-Wert die Wahrscheinlichkeit auf 100% und für alle anderen auf 0%.
Der Durchschnittsbürger verhält sich bei Spielangeboten wohl ähnlich wie Horst Hemmerling und seine Freunde, dennoch scheut er das hohe Risiko eines Überholvorgangs auf der Landstraße nicht, obwohl der dadurch herausgeschundene Zeitgewinn meist das erhöhte Risiko nicht aufwiegt. Fall 2 aus der Fallsammlung ist ein besonders drastisches Beispiel für solches Verhalten. Psychologische Experimente zeigen, dass Personen, die bei Gewinnaussichten risikoavers sind, sich im Falle von drohendem Schaden eher risikofreudig zeigen.
Für diese Personen hat die subjektive Schadensfunktion im Grunde dieselbe Form wie die Nutzenfunktion. Folglich wird der deterministische Schaden (Verzicht aufs Überholen) gegenüber dem zufälligen (möglicher Unfall) überbewertet. Also auch bei der Beurteilung von möglichen Schäden gibt es diese Tendenz zur Überbewertung der Gewissheit. Diese Tendenz hat den Rang eines allgemeinen psychologischen Prinzips.
Aber es gibt auch Ausnahmen: Sogar die bei Gewinnaussichten eher risikoscheue Leute spielen zuweilen Lotto. Und der risikofreudige Autofahrer hat eine Reihe von Versicherungen abgeschlossen - teils sogar recht unsinnige.
Auf den Standpunkt kommt es an
Unsere Risikotoleranz wird aber auch von Situationsfaktoren bestimmt: Der Fahrer schätzt das Risiko beim Überholen durchaus anders ein als sein Beifahrer. Hersteller und Betreiber eines Kernkraftwerks werden mit den Bürgerinitiativen der betroffenen Bürgern nicht über die Risikobewertung einig. Die Risikowahrnehmung wird durch persönliche und gesellschaftliche Gegebenheiten bestimmt. Die Risikobewertung ist folglich auch abhängig vom Standpunkt dessen, der die Bewertung durchführt. Es kommt darauf an, ob er Entscheider oder Betroffener ist, ob er Einfluss auf das Risiko hat oder nicht, ob er Fachmann ist oder Laie. Untersuchungen haben ergeben, dass die Risikowahrnehmung wesentlich durch
- die Bekanntheit einer Gefahr,
- die Freiwilligkeit im Eingehen eines Risikos und
- die Beeinflussbarkeit des Risikos
bestimmt wird. Auch hierfür ist Fall 2 der Sammlung ein anschaulicher Beleg: Die Leute von Folkestone beurteilen die gewählte Fahrtroute sicher ganz anders als der Frachterkapitän.
Risiken verteilen
Horst Hemmerling trifft im Foyer des Spielkasinos seinen Freund Gerd Grohe. Sie sprechen über das Jubiläumsangebot des Hauses. "Ich nehme das Angebot nicht an" sagt Horst. "Meine Risikobereitschaft reicht nicht aus. Wie wärs's wenn wir uns zusammentun. Wir spielen beide mit und teilen uns den Gesamtgewinn." Gerd versteht sofort: "Meine Risikobereitschaft ist nicht viel anders als deine. Allein würde ich auch nicht spielen. Vielleicht bringt uns dein Vorschlag weiter. Denn das Spielkasino sollten wir nicht ungerupft lassen." Sie machen sich ein Bild von der Entscheidungssituation: Wenn beide mitmachen, könnten beide gewinnen: Mit der Wahrscheinlichkeit von (1/6)2 streicht jeder von ihnen 7000 Euro ein. Wahrscheinlicher ist der Fall, dass genau einer von ihnen gewinnt. Das passiert mit der Wahrscheinlichkeit 2·(1/6)·(5/6). Dann erhält jeder 3500 Euro. Ansonsten gibt es nichts. Sie berechnen das Sicherheitäquivalent. Sie kommen auf einen Wert von 937 Euro. Das ist im Vergleich zum Einsatz noch zu wenig. Aber eine Idee ist geboren: Gerd und Horst ziehen den gemeinsamen Bekannten Fred Förster hinzu. Für die drei erscheint die Partie jetzt in einem anderen Licht. Horst Hemmerling ermittelt sein Sicherheitsäquivalent unter der Bedingung, dass sich alle drei beteiligen und den Gewinn aufteilen. Er kommt auf 1003 Euro. Das ist ihm genug. Er spricht sich für Teilnahme aus. Die anderen sehen es genauso.
Das Beispiel der Drei Spieler im Kasino wird im Excel-Arbeitsblatt
- Utility.xls behandelt. Außerdem wird anhand dieses Beispiels in die Analyse von Entscheidungssituationen mittels
- Entscheidungs-Ereignisbäumen eingeführt.
Werkzeuge zur Entscheidungsfindung
Das Excel-Arbeitsblatt Utility.xls
|
Bezeichnung |
Symbol |
|
Ankerwert |
x0 |
|
Minimum des objektiven Nutzens x |
min |
|
Maximum des objektiven Nutzens x |
max |
Das Excel-Arbeitsblatt Utility.xls erlaubt die Analyse des Nutzens oder Schadens von Entscheidungsalternativen. Zugrunde gelegt ist die Nutzenfunktion u(x) = c ln(1+(x-min)/x0). Die Konstante c ist so bestimmt, dass sich für den Maximalwert von x ein subjektiver Nutzen von 100 Prozent ergibt.
Die Eingabezellen des Arbeitsblattes sind grün unterlegt. Über die Parameter gemäß nebenstehender Tabelle kann die subjektive Nutzenfunktion festgelegt werden. Gibt man darüberhinaus die Wahrscheinlichkeitsverteilung des Nutzens ein, liefert das Arbeitsblatt den Wert des subjektiven Nutzenerwartungswerts und das Sicherheitsäquivalent.
Im Arbeitsblatt sind als Beispiel die Werte für die "Drei Spieler im Kasino" eingetragen.
Die Methode der Entscheidungs-Ereignisbäume
Die Analyse kleinerer Entscheidungs-Ereignisbäume ist mit der Tabellenkalkulation gut möglich. Wie man das mit System machen kann, zeige ich im Aufsatz "Putting the Normative Decision Model into Practice" am Beispiel eines mehrstufigen Entscheidungsproblems. Für die Analyse von Ereignisbäumen werden von verschiedenen Firmen Werkzeuge angeboten. Hinweise sind auf der Seite Zuverlässigkeit und Sicherheit zu finden.
Entscheidung bei begrenzter Rationalität
Bisher ging es ausschließlich um rationale Entscheidungen. Wir setzten voraus, dass wir alle möglichen Entscheidungsalternativen kennen, dass alle möglichen Konsequenzen der Entscheidungen sowie die Eintrittswahrscheinlichkeiten erfasst sind und dass die subjektiven Präferenzen klar zu Tage liegen.
Tatsächlich aber treffen wir Entscheidungen im Allgemeinen unter den Bedingungen begrenzter Rationalität.
· Wesentliche Entscheidungsalternativen sind uns möglicherweise gar nicht bewusst.
· Wir haben nicht immer sämtliche Konsequenzen im Sinn.
· Oft können wir Nutzen und Schaden nicht ausreichend genau beziffern.
· Das statistische Material für die Abschätzung der Wahrscheinlichkeiten reicht nicht aus.
· Es fehlen Zeit und Rechenkapazität für die notwendigen Kalkulationen.
Bewusst und auch unbewusst setzen wir Faustregeln (Heuristiken) ein und kommen so meist ohne große Rechnerei zu brauchbaren Entscheidungen. Aber auch von Fehlentscheidungen können wir ein Lied singen. Auf meiner Internet-Seite DENKFALEN UND PARADLOXA finden Sie eine ganze Reihe von Beispielen für die „Abkürzungen des Denkens“ und die daraus folgenden Irrungen.
Um unserer Schwierigkeiten beim Abschätzen von Wahrscheinlichkeiten geht es im Paradoxon von Simpson, im Xenophobie-Beispiel und in der Harvard-Medical-School-Studie, im Halbkreis-Experiment und beim Paradoxon der Restlebensdauer. Aber auch für die anderen Auswirkungen der begrenzten Rationalität lassen sich dort Beispiele finden. Hier werde ich der Sammlung ein paar Beispiele hinzufügen.
Aber beginnen will ich damit, dass es durchaus Auswege aus peinlichen, weil zu eng gesehenen, Entscheidungslagen gibt, und dass wir solche Auswege auch tatsächlich finden können.
Der Sprung heraus aus dem System
Im 19. Jahrhundert erlebte Paris zahlreiche Unruhen. Der Kommandant einer Gardeabteilung hatte den Befehl, einen mit Demonstranten gefüllten Platz unter Schusswaffengebrauch zu räumen. Er gab den Befehl, die Waffen durchzuladen und anzulegen. Die Menge erstarrte vor Entsetzen. Da zog der Kommandant seinen Säbel und rief: „Mesdames et Messieurs, ich habe den Befehl, auf die Canaille zu schießen. Da ich vor mir aber eine große Anzahl ehrenwerter Bürger sehe, bitte ich sie, wegzugehen, damit ich unbehindert auf die Canaille feuern kann.“ Kurze Zeit darauf hatte sich der Platz geleert.
Watzlawick, Weakland und Fisch (1992, S 104) analysieren die hier zum Ausdruck kommende Blickfelderweiterung: „Der Offizier hat eine drohende Menge vor sich. In der für Veränderungen erster Ordnung typischen Weise lautet sein Befehl, Gewalt mit Gewalt, also mit ‚mehr desselben’ zu begegnen. Da seine Leute bewaffnet sind und die Menge nicht, bestehen kaum Zweifel, dass ‚mehr desselben’ Erfolg haben wird. Aber im weiteren Kontext wäre diese Lösung nicht nur keine Lösung, sondern sie würde die bestehende Unruhe noch weiter anfachen. Durch sein geschicktes Vorgehen bewirkt der Offizier eine Veränderung zweiter Ordnung; er hebt die Situation aus dem Rahmen heraus, der bis zu diesem Augenblick sowohl ihn wie auch die Demonstranten enthielt und erzielt damit eine für alle Beteiligten annehmbare Umdeutung der Situation.“
Die Qual der Wahl
|
Qualitäten |
Kandidaten |
||
|
A |
B |
C |
|
|
Lebenswandel |
- |
0 |
+ |
|
Erfahrungen |
0 |
+ |
- |
|
Vorstellungen |
+ |
- |
0 |
In einem Städtchen ist der Bürgermeister neu zu wählen. Drei Kandidaten stellen sich zur Wahl: Astor, Ballheim und Chuntz - wir wollen sie kurz A, B und C nennen. Wir versetzen uns in die Lage eines Wählers. Gut gerüstet mit dem Wissen aus dem Kurs "Klug entscheiden bei Risiko" erstellt unser Wähler eine Tabelle der möglichen Konsequenzen seiner Wahl. Für ihn sind es drei Qualitäten, die den Kandidaten auszeichnen sollten: ein untadeliger Lebenswandel, ein großer Erfahrungsschatz und die richtigen politischen Vorstellungen. C hat einen sehr guten Leumund, der Lebenswandel von B ist so lala und über A hört man nichts Gutes. Hinsichtlich der Erfahrungen ist B allen anderen überlegen, C ist ein weitgehend unbeschriebenes Blatt und A liegt in der Mitte zwischen beiden. Die politischen Vorstellungen von A gefallen unserem Wähler sehr gut, kaum hingegen die des B; von C hat er noch nichts besonders Aufregendes gehört. Die Tabelle ist erstellt. Unser Wähler will denjenigen wählen, der den anderen in wenigstens zwei der drei Kriterien überlegen ist. Er geht nach dem K.-o.-Prinzip vor: B schlägt A in puncto Lebenswandel und Erfahrungen. C schlägt B hinsichtlich des Lebenswandels und der politischen Vorstellungen. Also ist C der Beste - oder?
Unser Wähler ist vorsichtig und vergleicht zusätzlich A mit C. Verblüfft stellt er fest, dass A sowohl hinsichtlich der Erfahrungen als auch bezüglich der politischen Vorstellung C überlegen ist. C kann also doch nicht der Beste sein. Wer dann?
Die Situation ähnelt dem Wählerparadoxon, auf das der Marquis de Condorcet 1758 aufmerksam gemacht hat (Condorcet-Effekt). Über Wahlsysteme und deren innere Widersprüche informiert das Web-Angebot Wahlrecht.
Äquivalent oder nicht?
Wir betrachten zwei Spiele (Kahneman/Tversky, 1979).
Spiel 1: Bei diesem Spiel kann sich der Spieler vorab für eine von zwei Varianten entscheiden. Er kann sich für die Alternative 1 entscheiden, in der 3000 Israelische Pfund mit einer Wahrscheinlichkeit 25% zu gewinnen sind, oder für Alternative 2, bei der es 4000 Pfund mit einer Wahrscheinlichkeit von 20% gibt. Grafik dazu.
Spiel 2: Das Spiel ist zweistufig. In der ersten Stufe ist die Wahrscheinlichkeit, nichts zu gewinnen, gleich 75%. Mit der Wahrscheinlichkeit von 25% tritt der Spieler in die zweite Stufe ein. In der zweiten Stufe hat der Spieler zwei Möglichkeiten. Er kann sich dafür entscheiden, sofort 3000 Pfund zu kassieren (Alternative 1) oder aber ein weiteres Spiel mitmachen (Alternative 2). In diesem zweiten Spiel sind 4000 Pfund zu gewinnen. Der Gewinn tritt mit 80% Wahrscheinlichkeit ein. Ansonsten geht der Spieler leer aus. Der Spieler muss sich vor dem Spiel für eine Alternative entscheiden, also noch bevor das Resultat der ersten Stufe bekannt ist. Grafik dazu.
Widerspruch: Schaut man sich die beiden Spiele genauer an, stellt man fest, dass sie vollkommen gleichwertig sind: Die Alternative 1 hat in beiden Spielen eine Gewinnerwartung von 750 Pfund. Sogar die Wahrscheinlichkeitsverteilung des Gewinns ist identisch. Und bei Alternative 2 ist die Gewinnerwartung ebenfalls identisch verteilt mit einem Erwartungswert von 800 Pfund. Psychologische Experimente haben ergeben, dass im 1. Spiel die meisten Versuchspersonen (65%) die objektiv günstigere Alternative 2 wählen. Im Falle des 2. Spiels wird diese Alternative nur noch von einer Minderheit (22 %) gewählt.
Erklärungsversuch: Dieser Widerspruch lässt sich nicht mit einer irgendwie verlaufenden Nutzenfunktion erklären. In der sequentiellen Formulierung des zweiten Spiels hat die 3000 Pfund-Alternative einen scheinbaren Vorsprung an Gewissheit.
Urlaub auf Hawaii
Das Examen ist geschrieben. Es bietet sich die Chance, zu äußerts günstigem Preis einen Urlaub auf Hawaii zu buchen. Letzte Gelegenheit dazu bietet sich heute. Das Ergebnis des Examens wird aber erst morgen bekanntgegeben. Wie lautet die Entscheidung? Wird gebucht oder nicht?
Widerspruch: Auf die Frage "buchen oder nicht?" antworteten viele der Befragten mit nein, obwohl sie sich sowohl im Falle eines bestandenen Examens als auch im Falle des Scheiterns - jeweils wohl aus anderen Gründen - für den Urlaub entscheiden würden.
Erklärungsversuch: Der Widerspruch wird darauf zurückgeführt, dass wir uns dagegen sträuben, Disjunktionen zu durchdenken. Wir neigen dazu, im Verzweigungspunkt eines Entscheidungsbaumes zu verharren.
Der Einrahmungs-Effekt
Im Beispiel "Äquivalent oder nicht?" ist eine Denkfalle wirksam, die als Framing Trap oder Framing Effect bekannt ist: Entscheidungen und Einschätzungen hängen von der Darstellung des Problems oder der Aufgabe ab ("Glas ist halbvoll", "Glas ist halb leer"). Der Einrahmungs-Effekt macht sich bemerkbar, wenn ein und dieselbe Entscheidungssituation einmal in der "Nutzenterminologie" und ein andermal in der "Schadensterminologie" präsentiert wird. Die Autoren des Buches Smart Choices, Hammond, Keeney und Raiffa, stellten erfahrene Versicherungsleute vor die folgende Entscheidung:
Stellen Sie sich vor, sie sind Schadensregulierer einer Versicherungsgesellschaft. Gestern sind vor Alaska drei Lastschiffe gesunken, deren Ladung versichert ist. Sie haben die Aufgabe, den Verlust an Ladung so gering wie möglich zu halten. Der Wert der Ladung eines jeden der Schiffe beträgt 200 000 $. Die Bergungsgesellschaft bietet Ihnen zwei Möglichkeiten, die gleich viel kosten: Plan A führt zur Bergung der Ladung eines Schiffes. Bei Plan B gibt es eine Wahrscheinlichkeit von 1/3, dass die Ladung aller drei Schiffe geborgen wird. Mit der Wahrscheinlichkeit von 2/3 wird nichts gerettet. Welchen Plan würden Sie wählen?
In der Befragung befürworteten 71 % der Leute den "weniger riskanten" Plan A.
Einer anderen Gruppe von Personen wurden folgende Pläne zur Auswahl vorgelegt: Plan C führt zum Verlust von zwei der drei Ladungen mit einem Wert von insgesamt 400 000 $. Plan D führt mit der Wahrscheinlichkeit von 2/3 zum Verlust aller drei Ladungen mit einem Gesamtwert von 600 000 $, aber er bietet eine Chance von 1/3, gar nichts zu verlieren.
In den Antworten stimmten jetzt 80 % der Leute für den "riskanteren" Plan D. Dabei unterscheiden sich die Pläne A und C nicht. Dasselbe gilt für die Pläne B und D. Die widersprüchlichen Antworten machen deutlich, dass die meisten Leute risikoscheu sind, wenn es um Gewinne und Nutzen geht, aber risikofreudig, wenn es darum geht, Schäden oder Verluste zu vermeiden. Siehe: Gleichzeitig risikoscheu und risikofreudig.
Veröffentlichungen
Grams, T.: Grundlagen des
Qualitäts- und Risikomanagements. Zuverlässigkeit, Sicherheit, Bedienbarkeit.
Vieweg Praxiswissen, Braunschweig,
Wiesbaden 2001
Grams, T.: Denkfallen und Programmierfehler. Springer, Heidelberg 1990
Grams, T.: Technisches und "menschliches" Versagen - ein Abgrenzungsproblem. VDI/VDE-GMA Aussprachetag "Sicherheitstechnik und Automatisierung", Langen 10./11. April 1997. VDI Berichte 1336. VDI Verlag, Düsseldorf 1997
Grams, T.: Bedienfehler und ihre Ursachen.
- Teil 1. Automatisierungstechnische Praxis atp 40 (1998) 3, S. 53-56
- Teil 2. Automatisierungstechnische
Praxis atp 40 (1998) 4, S. 55-60
Grams, T.: Operator Errors and their Causes. In: Computer
Safety, Reliability and Security. Proceedings of the 17th International
Conference, SAFECOMP '98,
Grams, T.: Putting the Normative Decision Model into Practice.
In: Elzer, P. F.; Kluwe, R. H.; Boussoffara, B. (Eds): Human Error and System
Design and Management. Lecture Notes in Control and Information Sciences 253.
Springer, London 2000, S. 99-107
Diplomarbeit
Geisen, O.: Java-Anwendung zur Darstellung und Analyse komplexer Entscheidungssituationen. Diplomarbeit im Fachbereich Elektrotechnik der Fachhochschule Fulda, 18. Mai 2000.
Literatur
Populärwissenschaftliche Werke
Bernstein, P. L.: Against the Gods. The remarkable story of risk.
Wiley,
Cube, F. von: Gefährliche Sicherheit. Die Verhaltensbiologie des Risikos. Hirzel, Stuttgart 1995. "Motorradfahrer fühlen sich aufgrund ihrer Qualifikation sicher, sie empfinden das objektive Risiko, das ihnen durchaus bekannt ist, subjektiv nicht als solches. Einige Fahrer holen sich freilich noch eine zusätzliche Sicherheit: Sie glauben an einen 'Schutzengel'" (S. 41).
Grams, T. (Hrsg.): Risiko - Unser Umgang mit der Angst. Tagungsband des 7. Fuldaer Elektrotechnik-Kolloquiums, 18.10.2002. PDF-Datei (210 KB)
Hammond, J. S.; Keeney, R.
L.; Raiffa, H.: Smart Choices.
Wellmann, K.-H.; Thimm, U. (Hrsg.): Intelligenz zwischen Mensch und Maschine. Begleitbuch zum Neuen Funkkolleg "Die Zukunft des Denkens". LIT, Münster 1999. Enthält einen Auszug aus "Der Ursprung des Bewußtseins" von J. Jaynes: "Odysseus - ein Held ohne Bewußtsein?".
Einführungen, Überblicke, Sammelwerke
Bamberg, G.; Coenenberg, A.: Betriebswirtschaftliche Entscheidungslehre. Vahlen, München 1989. Entscheidungen bei Risiko. Bernoulli-Prinzip und Nutzenfunktion. Risikoaversion, Risikosympathie. Empirische Ermittlung des Bernoulli-Nutzens. Sicherheitsäquivalent. Mehrstufige Entscheidungen. Gremienentscheidungen: Wählerparadoxon (Condorcet-Effekt).
Bechmann, G. (Hrsg.): Risiko und Gesellschaft.
Grundlagen und Ergebnisse der interdisziplinären Risikoforschung.
Westdeutscher Verlag, Opladen 1993. "Stützung der Annahme ..., daß die
Freiwilligkeit ein Schlüsselfaktor für die Akzeptanz sei ... Facetten wie die
Bekanntheit, die Kontrollierbarkeit, die Gerechtigkeit der Verteilung und
insbesondere das Katastrophenpotential beeinflussen ebenfalls die
Akzeptanz" (Helmut Jungermann, Paul Slovic, S. 196). "Was die eigenen
Entscheidungen angeht, ist man oft extrem risikobereit: Man fährt Auto oder
sogar Motorrad, man klettert auf Berge, man heiratet. Bei Gefahren, die einem
von anderer Seite zugemutet werden, ist man dagegen hochempfindlich ...
Übersetzt in das Thema Moral heißt dieser 'double standard': Es gibt keine
sinnvolle Anwendung für die Maxime der Reziprozität ... Wenn noch gälte: 'Liebe
Deinen Nächsten wie Dich selbst', könnte dieser sich auf allerhand gefaßt
machen" (Niklas Luhmann, S. 330).
Renn, O.; Zwick, M. M.: Risiko- und Technikakzeptanz. Springer, Berlin, Heidelberg 1997. Herausgeber ist die Enquete-Kommission "Schutz des Menschen und der Umwelt" des 13. Deutschen Bundestages. Themen: Risiko- und Technikakzeptanz. Risiko- und Technikkommunikation.
Wissenschaftliche Werke
Elzer, P. F.; Kluwe, R. H.;
Boussoffara, B. (Eds): Human Error and System Design
and Management. Lecture Notes in Control and Information Sciences 253.
Springer, London 2000. "The available normative decision theory is a
solid base from which to build a theory of how humans actually decide"
(Thomas B. Sheridan, S. 6).
Kahneman, D.; Slovic, P.;
Tversky, A. (eds.): Judgment under uncertainty:
Heuristics and biases. Cambridge University Press, Cambridge CB2
1RP, 1982. Enthält den titelgleichen wegweisenden Aufsatz von Tversky und
Kahneman aus dem Jahre 1974.
Kahneman, D.; Tversky, A.: Prospect Theory: An Analysis of Decision under Risk.
Econometrica, 47 (March, 1979) 2, 263-291. "Outcomes which are obtained
with certainty are overweighted relative to uncertain outcomes. In the positive
domain, the certainty effect contributes to a risk averse preference for a sure
gain over a larger gain that is merely probable. In the negative domain, the
same effect leads to risk seeking preference for a loss that is merely probable
over a smaller loss that is certain. The same psychological principle - the
overweighting of certainty - favors risk aversion in the domain of gains and
risk seeking in the domain of losses" (S. 268-269).
Nisbett, R. E. (edt.): Rules for Reasoning. Erlbaum,
Perrow, C.:
Shafir, E.: Uncertainty and the difficulty of thinking through
disjunctions. Cognition 50 (1994) 1-3, 403-430). Enthält
"Urlaub auf Hawaii" und andere Beispiele zur Schwierigkeit,
Entscheidungsbäume konsequent zu durchdenken.
Watzlawick, Paul; Weakland, John
H.; Fisch, Richard: Lösungen. Zur Theorie und Praxis
menschlichen Wandels. Verlag Hans Huber, Bern, Göttingen, Toronto 1992. Unter
bestimmten Umständen (ist) das Entstehen von Problemen die unmittelbare Folge
falscher Lösungsversuche einer
bestehenden Schwierigkeit (S. 56). Lösungen zweiter Ordnung heben die zu
lösende Situation aus dem paradoxen, selbstrückbezüglichen Teufelskreis heraus,
in den sie die bisherigen Lösungsversuche geführt haben, und stellen sei in
einen neuen, weiteren Rahmen (S. 105).
Internet-Verbindungen
Entscheidungsanalyse: Web-Angebot des Dresdner Instituts für Arbeitsberatung und Arbeitsforschung
EADM:
European Association for Decision Making
SJDM:
Society for Jugment and Decision Making
Decision Analysis Society of INFORMS
Expert Choice: Tool zur Entscheidungshilfe
© Timm Grams, 08.09.00 (zuletzt aktualisiert: 14.02.07)