Spektakuläres aus der Wissenschaft
„Koreanische Wissenschaftler haben eine neue Anwendung für die Kunst des Handlesens entdeckt – angesichts der Finger ihrer männlichen Probanden vermochten die Forscher um Kim Tae Beom vom Gachon University Gil Hospital deren Penislänge einzuschätzen. Je kleiner der Quotient aus den Längen von Zeige- und Ringfinger der rechten Hand, desto stattlicher der Penis, berichten die Wissenschaftler…“ So steht es im Nachrichtenmagazin „Der Spiegel“ unter dem reißerischen Titel „Finger verrät Penislänge“, Ausgabe 27/2011, Seite 120.
Da haben wir wieder einmal eine jener vermeintlich spektakulären wissenschaftlichen Entdeckungen, die von den Medien so gerne an die große Glocke gehängt werden. Für Partygespräche mag so etwas gut sein. Aber was steckt dahinter? Ist es für den Hausgebrauch – im Swingerclub beispielsweise – von irgendwelchem Nutzen? Sehen wir doch einmal genauer nach.
Was wurde tatsächlich herausgefunden?
Der Spiegel gibt die qualitativen Aussagen des Originalartikels „Second to fourth digit ratio: a predictor of adult penile length“ korrekt wieder. Aber solche qualitativen Aussagen sind im Grunde belanglos.
Grundsätzlich liefern statistische Studien quantitative Ergebnisse, die etwas darüber aussagen, wie groß und wie deutlich der gefundene Effekt ist. Wenn wir verstehen wollen, was bei der Studie, über die hier berichtet wird, wirklich herauskam, müssen wir uns demnach mit Zahlen beschäftigen. Etwas Mathematik ist zum Verständnis unerlässlich. (Die Mathematik, von der hier die Rede ist, sollte zumindest zukünftig zur mathematischen Allgemeinbildung zählen.)
Es geht um den statistischen Zusammenhang zweier Größen. Aus der Stichprobe der 144 Männer wurden für die untersuchten Größen Schätzwerte für Mittelwert (Erwartungswert) und Standardabweichung ermittelt. Die folgende Tabelle zeigt diese Werte.
Den Zusammenhang zwischen den beiden Größen beschreibt der Korrelationskoeffizient. Die Studie ergab den Wert r = −0.216.
Ein kleines Experiment
Was sagen uns diese Zahlen über Größe und Deutlichkeit des Zusammenhangs? Um das zu klären, schiebe ich ein kleines Rechenexperiment ein, das sich mit einem ganz normalen Tabellenkalkulationsprogramm (beispielsweise Excel) durchführen lässt: Regression.xls.
Die Deutlichkeit des Zusammenhangs lässt sich daran ermessen, inwieweit sich das gefundene Ergebnis von einem reinen Zufallsfund abhebt. Wir gehen also erst einmal von der Hypothese aus, dass es keinen Zusammenhang zwischen den beiden untersuchten Größen gibt (Nullhypothese). Für unser kleines Experiment nehmen wir an, dass die Größen einer Normalverteilung unterliegen. Durch Mittelwert und Standardabweichung sind die den Größen zugeordneten Zufallsvariablen eindeutig bestimmt.
Ich erzeuge eine Stichprobe aus 144 Wertepaaren der uns interessierenden Größen mit dem Zufallsgenerator und trage diese in eine xy-Grafik ein — auf der x-Achse die Werte der Einflussgröße (Quotient der Fingerlängen, Digit ratio) und auf der y-Achse die jeweils zugehörigen Werte der Zielgröße (Penislänge, Penile length).
Die Regressionsgerade (linearer Trend) hat eine Steigung, die proportional zum ermittelten Korrelationskoeffizienten ist. Wohlgemerkt: Die Wertepaare sind jeweils voneinander statistisch unabhängig und der Korrelationskoeffizient ist nach den Regeln der Wahrscheinlichkeitsrechnung gleich null. Wegen der endlichen Stichprobengröße ergeben sich Zufallswerte, die meist ein wenig von null abweichen (vorgetäuschte Korrelation).
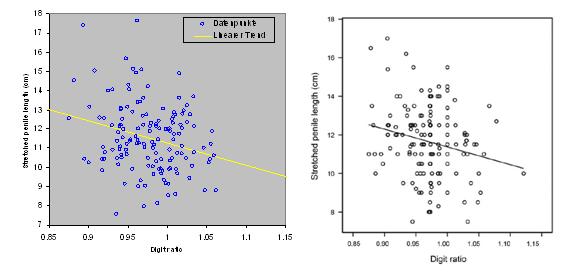
Nach ein paar Experimenten (etwa zehn bis zwanzig Neuberechnungen des Arbeitsblattes) erscheint eine Grafik, die derjenigen der Originalveröffentlichung verblüffend ähnlich sieht. Der Korrelationskoeffizient beträgt in dem von mir gefundenen Fall sogar -0.26. Das folgende Bild zeigt links mein Ergebnis und rechts das der Studie.
Offenbar lässt sich nicht ausschließen, dass es sich bei dem Ergebnis der Studie um einen reinen Zufallsfund handelt.
Die Autoren haben ihr Ergebnis als signifikant (nur ein anderes Wort für deutlich) eingestuft, sehen es also nicht als Zufallsfund an. Dabei legen sie, wie in solchen Studien üblich, ein Signifikanzniveau von 5% zugrunde. Das heißt: Unter zwanzig Zufallsergebnissen findet sich im Mittel eins, das in diesem Sinne signifikant ist. Oder so: Der Zufall produziert mit 5-prozentiger Wahrscheinlichkeit „signifikante“ Ergebnisse.
Als Faustregel kann gelten: Wenn das Quadrat des Korrelationskoeffizienten, das sogenannte Bestimmtheitsmaß, den Kehrwert des um eins verminderten Stichprobenumfangs um wenigstens den Faktor vier übersteigt, dann ist der Zusammenhang signifikant auf dem 5%-Niveau. Bei der hier vorliegenden Stichprobengröße von 144 und dem Korrelationskoeffizienten r = −0.216 ist die Bedingung erfüllt.
Die Faustregel sagt uns darüber hinaus, dass mit sehr großen Stichproben auch ziemlich kleine Korrelationen deutlich erkennbar sind. Ich komme noch darauf zurück.
Interpretation der Grafiken und der Zahlen
Selbst wenn Zweifel bleiben: Wir nehmen das gefundene Ergebnis als einen deutlichen Hinweis auf den Zusammenhang. Das fällt auch deshalb leicht, weil dem Bericht über die Studie zu entnehmen ist, dass es kein Fishing for Significance gegeben hat: Es wurden also nicht viele verschiedene Einflussgrößen (Länge der Nase, Schuhgröße, Größenverhältnisse aller möglichen Finger- und Zehenpaarungen, usw.) untersucht und aus der Menge der Befunde dann der mit dem deutlichsten Zusammenhang ausgewählt. Bei einem solchen Vorgehen wäre es nämlich nahezu unausweichlich, einen zufällig vorgetäuschten „signifikanten“ Zusammenhang zu finden.
Aber wie steht es um die Größe des Einflusses? Da sieht es tatsächlich ziemlich mager aus: Das Quadrat des Korrelationskoeffizienten, das Bestimmtheitsmaß also, ergibt für die Studie den Wert 4.7%.
Das Bestimmtheitsmaß ist gleich dem Anteil der Varianz der Zielgröße, der durch den linearen Trend erklärt wird. Hier sind das weniger als fünf Prozent. Die Grafiken geben beredtes Zeugnis, wie wenig eine Prognose auf Basis des Größenverhältnisses der Finger mit den tatsächlich stark schwankenden Werten zu tun hat.
Fazit
Ja, es kommt auf die Größe an. Auf die Größe des Zusammenhangs. Die Studie hat einen möglicherweise tatsächlich vorhandenen Effekt gezeigt. Aber er ist winzig und für Vorhersagen unbrauchbar. In der Tat: Size matters.