Ohne Zweifel haben polizeiliche Kriminalstatistiken (PKS) ihren Nutzen. Fragwürdig wird die Sache erst, wenn Politik und Öffentlichkeitsarbeit ins Spiel kommen: Dann wird ausgewählt, verdichtet und grafisch herausgeputzt, bis die gewünschte Nachricht passend untermauert ist. Und das geht ganz ohne Fälschung.
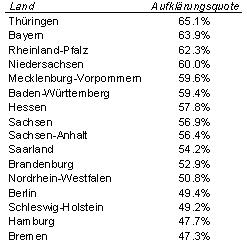
Der Manipulant weiß, dass sich das Publikum durch Rangfolgen leicht beeindrucken lässt. Das umfangreiche Zahlenwerk der PKS lässt sich beispielsweise zu einer Tabelle zusammenkochen. Wir erhalten eines der beliebten Rankings, hier einmal eine Sortierung der Bundesländer nach polizeilichem Aufklärungserfolg (BKA).
Solche Rankings befeuern die politische Diskussion. Sie genießen eine Wertschätzung, die ihnen genau genommen nicht zukommt. Es handelt sich meist um ziemlich sinnleere Zahlenspielereien. Ein Beispiel sind die heute so geschätzten Hochschulrankings. Aber darüber später, in einem eigenen Artikel. Hier will ich nur zeigen, wie man sich ein persönliches Ranking zusammenbasteln kann. Und dieses Ranking wird auch nicht sinnloser sein als das von interessierter Seite veröffentlichte.
Wir bleiben hier einmal bei den Kriminalstatistiken. Was bei den Kriminalitätsstatistiken funktioniert, geht auch mit beliebigen anderen Statistiken, soweit sie mehrere – womöglich gegeneinander konkurrierende – Institutionen betreffen und wenn die Bewertung in mehrere Kategorien zerfällt.
Aus Osthessen kommt diese Stellungnahme zur Kriminalstatistik 2010: „Bei einem deutlichen Straftatenrückgang von 4.4 Prozent … konnte das Polizeipräsidium Osthessen seine Rekordaufklärungsquote des Vorjahres von 63,4 Prozent noch einmal um 0,2 Prozentpunkte auf 63,6 Prozent steigern. Dies ist die beste Aufklärungsquote seit Bestehen des Polizeipräsidiums Osthessen, betont Polizeipräsident Alfons Georg Hoff anlässlich der Vorstellung der Polizeilichen Kriminalstatistik (PKS) 2010.“
Das Polizeipräsidium Nordhessen kommentiert ihre Kriminalstatistik 2010 folgendermaßen: „Neben dem kontinuierlichen Rückgang der erfassten Straftaten sinkt auch Jahr für Jahr die sogenannte Häufigkeitszahl… Gleichzeitig stieg gegenüber dem Vorjahr die Aufklärungsquote nochmals um 0,3 Prozentpunkte auf jetzt 58,2 Prozent.“ (Eckhard Sauer, Polizeipräsident)
Die Aufklärungsquoten des Jahres 2010 lassen sich der Kriminalstatistik entnehmen.
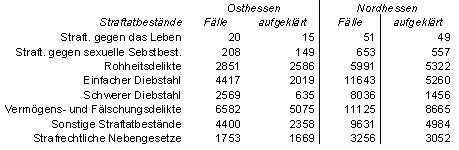
Bei kreativer Auslegung der Statistik könnte die nordhessische Polizei im direkten Vergleich mit den osthessischen Kollegen besser aussehen. Denn: In die Aufklärungsquote gehen alle Straftaten unterschiedslos ein. Aber ist es wirklich angemessen, einen einfachen Diebstahl genauso zu werten wie einen Mord?
Hätten die Nordhessen beispielsweise jeden Mord oder Tötungsversuch 1000-fach, die sexuellen Straftaten und die Rohheitsdelikte je 100-fach und alle anderen einfach gezählt, käme für sie eine Aufklärungsquote von etwa 87 Prozent heraus, und die läge leicht über der entsprechenden Aufklärungsquote der Osthessen.
Das Beispiel mag konstruiert erscheinen. Aber es illustriert die alltägliche Praxis im Rankinggeschäft. Denn die Rangfolgen hängen ganz entscheidend von der Auswahl und Gewichtung der Einflussgrößen und Kategorien ab. Ein Musterbeispiel dafür ist die fragwürdige Auswahl und Gewichtung von Daten im Zukunftsatlas des Prognos-Instituts, der die deutschen Regionen in eine Rangordnung bezüglich ihrer Zukunftsfähigkeit bringt.
Dass die Schwierigkeiten mit Reihenfolgeproblemen grundsätzlicher Natur sind, hat der Marquis de Condorcet bereits 1758 publik gemacht (Wählerparadoxon, Condorcet-Effekt). Ian Stewart bringt in seinem Buch „Professor Stewarts mathematisches Kuriositätenkabinett“ von 2010 eine dazu passende Denksportaufgabe. Ich sags mal so: Sie werden von Ihrem Freund zu einem Würfelspiel eingeladen. Er lässt Ihnen den Vortritt und bietet Ihnen an, einen von drei Würfeln auszuwählen. Er will sich dann einen von den übrigen nehmen. Die Auswahl ist nicht trivial, denn die Augenzahlen sind etwas sonderbar: Einer der Würfel hat zwei Dreien, zwei Vieren und zwei Achten, der zweite hat zwei Einsen, zwei Fünfen und zwei Neunen, und der dritte zwei Zweien, zwei Sechsen und zwei Siebenen. Welcher der Würfel bietet Ihnen die besten Chancen, eine höhere Punktzahl zu erwürfeln als Ihr Freund? Klugerweise nehmen Sie an, dass Ihr Freund aus den verbleibenden Würfeln den für ihn günstigsten auswählt.