Den Leuten, die einen Blick in die Zukunft wagen, verdanken wir wunderbare Visionen: Bücher und Filme breiten vor uns Phantasiewelten aus. Darin gibt es Roboter, die den Menschen an Kraft und Intelligenz überlegen sind. Angefangen hat es wohl 1950 mit den Kurzgeschichten „I, Robot“ von Isaac Asimov.
Noch bevor sein erster Computer funktionsfähig war, ahnte Konrad Zuse, „dass es eines Tages Rechenmaschinen geben würde, die den Schachweltmeister besiegen können“ (Der Computer – Mein Lebenswerk. 1984). Heute ist es Geschichte: Im Jahr 1996 gelang es dem Schachcomputer Deep Blue, den amtierenden Schachweltmeister Garri Kasparow zu schlagen.
Und das ist noch lange nicht alles. Die Nachricht dieses Jahres ist der Sieg des Supercomputers Watson in der US-Quizshow „Jeopardy“.
Es sieht danach aus, als würden die Phantasien Wirklichkeit. Zumindest gibt es gestandene Wissenschaftler und Unternehmer, die fest daran glauben. Sie haben sich in der Singularitätsbewegung (Singularity Movement) zusammengefunden und ziehen in letzter Zeit ziemlich viel Aufmerksamkeit auf sich. Die Wochenzeitung TIME widmet ihr in der Ausgabe vom 21. Februar 2011 einen großen Bericht.
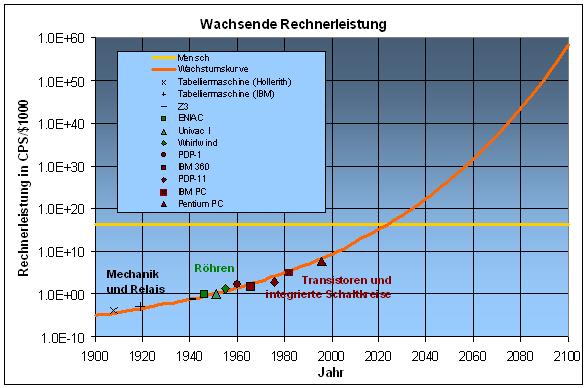
Auskunft über das Wesen der Bewegung erhalten wir von Ray Kurzweil, ihrem zurzeit wortmächtigsten und einflussreichsten Vertreter. Zentral in Kurzweils Argumentation ist eine Grafik; darin sind 49 Rechner und Computer des zwanzigsten Jahrhunderts nach ihren Erscheinungsjahren erfasst. Jede der Maschinen wird in der Grafik durch einen Punkt repräsentiert, dessen Lage durch die Anzahl der Instruktionen pro Sekunde festgelegt ist, die man für jeweils 1000 Dollar erhält. Kurzweil vergleicht diese Punktwolke mit dem Gesetz von Moore, das schon seit einigen Jahrzehnten als relativ stabile Aussage über das exponentielle Wachstum der Computerleistung gilt.
Kurzweil weist darauf hin, dass das Gesetz von Moore wohl für die integrierten Schaltungen gelte, aber dass es von der Mechanik über die Relaisschaltungen, die Röhren- und Transistortechnik bis hin zu den integrierten Schaltungen eine Reihe von Technologiewechseln gab und dass das Wachstum über alle diese Phasen hinweg sogar stärker als exponentiell sei.
Kurzweil veranschaulicht den Effekt der wachsenden Wachstumsrate („law of accelerating returns“) in einer Grafik. Durch die Punktwolke der logarithmisch über der Zeit aufgetragenen Rechnerleistungen legt er einen flotten aufwärts gerichteten Bogen. Er verlängert den Bogen weit über die Punktwolke hinaus und dehnt diesen kühnen Nike-Schwung auf das 21. Jahrhundert aus. Die folgende Grafik basiert auf Kurzweils Daten (Homo s@piens von 1999 und www.kurzweilai.net/the-law-of-accelerating-returns).
Darrell Huff (How to lie with statistics, 1954) nennt so etwas „Gee-Whizz Graphs“: grafisch aufgedonnerte Banalitäten.
Das Bild lässt nach Meinung der Singularitätsanhänger klar erkennen, ab wann der Computer den Menschen bezüglich Intelligenz überflügeln und dann an dessen Stelle die kulturelle Evolution vorantreiben werde. Es geschehe in etwa ab dem Zeitpunkt, zu dem die Wachstumskurve die Gerade „Mensch“ schneidet, also ab 2023. Danach werde es ziemlich bald zu einer Singularität kommen – zu einem Bruch in der Geschichte der Menschheit aufgrund des raschen und grundlegenden technischen Wandels.
Derartige punktgenaue Prognosen sind eigentlich eine Angelegenheit der Weltuntergangspropheten. Diesmal soll der Knall nach oben losgehen.
Kurzweils Daten habe ich nicht im Detail überprüft. Aber ich will doch kurz auf ein paar Dinge eingehen, die mir im Vorübergehen aufgefallen sind. Danach komme ich auf die Wachstumskurve zurück.
- Warum soll die Bitzählerei irgendetwas über die Intelligenz aussagen? Man weiß doch noch gar nicht, was Intelligenz überhaupt ist und wie man sie messen soll. Andererseits war bereits Zuses Z3 dem Menschen bezüglich Rechengeschwindigkeit und Genauigkeit weit überlegen. Und wer wissen will, wie weit die Wissenschaft der künstlichen Intelligenz nach Jahrzehnten größter Anstrengungen heute ist, der sollte sich diesen Artikel einmal maschinell ins Englische und dann wieder zurück ins Deutsche übersetzen lassen.
- Was die Kosten angeht, wird Zuses Z3 in eine Reihe mit dem IBM-PC gebracht. Aber der PC ist ein Massenprodukt und die Z3 war nie käuflich zu erwerben.
- Die Intelligenz des ENIAC wird höher eingestuft als die der Z3. Aber der ENIAC war, anders als die Z3, gar nicht frei programmierbar.
Nun zurück zur Wachstumskurve. Ich verrate Ihnen jetzt, wie Sie eigenhändig exponentielles Wachstum aus dem Nichts erzeugen können. Sie kennen sicherlich die Zahlenrätsel, bei denen man eine Folge von Zahlen geeignet fortsetzen soll. Die Aufgabe besteht darin, ein Bildungsgesetz für die Folge zu erkennen. Nehmen wir einmal die Folge 1, 3, 7, … Sie werden schnell erkannt haben, dass es sich um Zweierpotenzen minus eins handelt. Sie setzen diese Folge folgendermaßen fort: 1, 3, 7, 15, 31, 63, 127, 255, 511, 1023, …
Aber hoppla, es geht auch anders. Sie wissen, dass sich zu drei vorgegebenen Punkten immer ein Polynom zweiten Grades finden lässt, das diese Punkte genau trifft. Also konstruieren Sie sich ein solches Polynom. (Die unabhängige Variable durchläuft dabei die Platznummern der Zahlenfolge.) Sie erhalten jetzt die Folge 1, 3, 7, 13, 21, 31, 43, 57, 73, 91, …
Jetzt brauchen Sie nur noch die beiden Zahlenfolgen voneinander abzuziehen und können sich über dieses Resultat freuen: 0, 0, 0, 2, 10, 32, 84, 198, 438, 932, … Sie haben mit einer einfachen Funktion aus drei vorgebenen Nullen tatsächlich ein exponentielles Wachstum erzeugt. Und das können Sie noch weiter treiben. Sind Ihnen vier Nullen oder gar fünf oder sechs oder … gegeben: Stets finden Sie eine einfache Funktion, die nach diesen Anfangswerten exponentiell ins Unendliche strebt.
Ich hoffe, dieses Zahlenexperiment hat Ihr Vertrauen in kühne Prognosen etwas erschüttert.