Hoppla!
In einem Lehrbuch zum Thema Software-Verifikation finde ich den fett hervorgehobenen Satz: „Der Test von Hypothesen geht über die Falsifizierung ihres Komplements“. Dann wird gezeigt, dass bei einem Sachverhalt, der im Widerspruch zur Hypothese steht, der Test schlimmstenfalls mit einer geringen Wahrscheinlichkeit (von sagen wir 5%) bestanden wird. Aus dem Bestehen des Tests wird dann gefolgert, dass der angenommene Sachverhalt, die Alternativhypothese, unwahrscheinlich ist (5%) und die Hypothese entsprechend wahrscheinlich (95%).
Bei der Berechnung der Wahrscheinlichkeiten wurde die Alternativhypothese, die übrigens gar nicht das Komplement der Hypothese sein muss, als fest gegeben vorausgesetzt. Es geht also gar nicht um die Wahrscheinlichkeit der Alternativhypothese und schon gar nicht um die Wahrscheinlichkeiten von Hypothese und deren Komplement.
Irrtümer dieser Art sind selbst in der Fachwelt nicht selten. Wahrscheinlichkeiten treten unter verschiedenen Rahmenbedingungen in Erscheinung und sie sind dementsprechend auch verschieden definiert. Wer das nicht beherzigt, fällt herein.
Hier will ich Wahrscheinlichkeiten in die ihnen zukommenden Zusammenhänge stellen. Das soll helfen, Denkfallen der Statistik und Wahrscheinlichkeitsrechnung rechtzeitig zu entdecken und irrige Interpretationen zu entlarven.
Den letzten Anstoß zu diesem Hoppla!-Artikel gab das Buch „The Skeptics’ Guide to the Universe“ von Steven Novella (2018), in dem er sich u. a. auf die Arbeiten von Regina Nuzzo beruft. Novella beklagt, dass der p-Wert einer Studie oft als Wahrscheinlichkeit für das Nichtvorliegen des untersuchten Sachverhalts (z. B.: „das Medikament ist wirksam“) genommen wird, dass also die Hypothese über das Vorliegen des vermuteten und zu prüfenden Sachverhalts eine Wahrscheinlichkeit von 1-p haben muss. In klinischen Studien wird im Sinne eines schwachen Signifikanzniveaus oft ein Wert von p = 5% zugrunde gelegt, was für den zu prüfenden Sachverhalt eine Wahrscheinlichkeit von 95% nahelegen würde.
Solche Studien liefern nur Folgendes: Bei vorausgesetzter Nullhypothese besitzt das tatsächlich ermittelte Testergebnis zugunsten des zu prüfenden Sachverhalts eine nur geringe Wahrscheinlichkeit von p. Wir können die Nullhypothese also getrost verwerfen. Die Nullhypothese ist so gebildet, dass sie den zu testenden Sachverhalt, die zu prüfende Hypothese, ausschließt (Sachs, 1992, S. 185f.). Damit ist der zu prüfende Sachverhalt weiter im Rennen. Was wir aus dem Testergebnis nicht erfahren, ist die Wahrscheinlichkeit dafür, dass der zu testende Sachverhalt im Rahmen des Tests anwesend ist.
Beispiel: Psi-Test Würzburg 1-aus-10
Für die Konkretisierung der eben gemachten Aussagen wähle ich einen gut dokumentierten Test, nämlich den 1-aus-10-Test, den die Gesellschaft zur wissenschaftlichen Untersuchung von Parawissenschaften (GWUP) bisher 37mal in Würzburg durchgeführt hat. Ich habe die Daten von Soehnle (2014) um die seither durchgeführten Tests ergänzt.
Geltungsanspruch und Testbedingungen
Zu diesen Tests mit Aussicht auf ein Preisgeld können sich Personen melden, die sich für Psi-begabt halten: Wünschelrutengänger, Wahrsager usw.
Ein Beispiel: Im Jahr 2016 war unter den Kandidaten eine Homöopathin, die angab, Verunreinigung in Pflanzenerde erkennen zu können. Für den Test füllen die Versuchsleiter zehn Petrischalen mit Blumenerde. In einer davon ist – für die Kandidatin unsichtbar – kontaminierte Erde. Die Kandidatin muss nun ihre Fähigkeit nachweisen, indem sie die Schale mit kontaminierter Erde herausfindet. Das ist der Findevorgang. Dies wird dreizehn Mal gemacht. Der Stichprobenumfang je Test ist also gleich 13. Der Test ist bestanden, wenn der Kandidat wenigstens sieben Treffer vorzuweisen hat. Das ist das Testkriterium.
In allen anderen der insgesamt 37 von der GWUP durchgeführten 1-aus-10-Tests ging es vergleichbar zu.
Nullhypothese
Die Nullhypothese wird als Alternative zum Geltungsanspruch definiert und aus den allgemein akzeptierten Gesetzmäßigkeiten hergeleitet. Maßgabe ist also der Stand der Wissenschaft und nicht etwa eine übergeordnete Ontologie.
Die Nullhypothese im Falle des 1-aus-10-Tests besteht darin, dass bei sorgfältiger Versuchsdurchführung das Indifferenzprinzip gilt: Das Versteck wird bei jedem der dreizehn Findevorgänge rein zufällig mit einer Trefferwahrscheinlichkeit von 10% gefunden.
Interpretation des Tests
Das Bestehen und Nichtbestehen des Tests ist eine Sache des Zufalls. Es kann durchaus sein, dass ein paranormal Begabter fälschlich übersehen wird, weil er das Testkriterium zufälligerweise nicht erfüllt. Diesen Fall nennt man einen Fehler zweiter Art, anschaulich: „Übersehfehler“. Auf der anderen Seite steht die Möglichkeit, dass einem paranormal Unbegabten paranormale Fähigkeiten attestiert werden, weil er aus purem Zufall das Testkriterium erfüllt. Das ist ein Fehler erster Art, anschaulich: „Vortäuschungsfehler“.
Das Testkriterium muss sowohl die Interessen des Kandidaten an einer möglichst geringen Wahrscheinlichkeit für einen Fehler zweiter Art berücksichtigen, aber auch die Interessen der GWUP an einer möglichst geringen Wahrscheinlichkeit für einen Fehler erster Art.
Die Wahrscheinlichkeit für den Fehler erster Art („Vortäuschungsfehler“) wird in der mathematischen Statistik mit α bezeichnet, und die Wahrscheinlichkeit für einen Fehler zweiter Art („Übersehfehler“) mit β.
Wichtig ist also die Festlegung der Bedingungen für das Bestehen des Tests derart, dass sowohl der Fehler erster Art („Vortäuschungsfehler“) als auch der Fehler zweiter Art („Übersehfehler“) möglichst unwahrscheinlich werden. Wir suchen also nach Testkriterien mit möglichst kleinen oder zumindest ausbalancierten Werten für α und β. Die Wahrscheinlichkeit α ist das Signifikanzniveau des Tests und 1- β ist die Power des Tests.
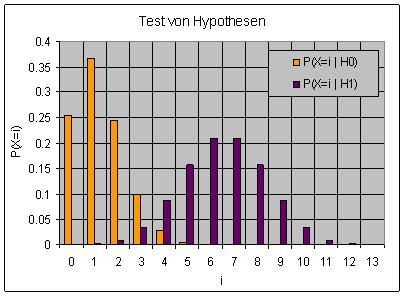
Wir nehmen zunächst einmal an, dass der Bewerber paranormal unbegabt ist (Nullhypothese H0). Die Trefferzahlen je Test mit jeweils 13 Findevorgängen folgen der (13, 10%)-Binomialverteilung.
Eine auf lange Sicht erzielte Trefferwahrscheinlichkeit von 50% spricht für paranormale Fähigkeiten (H1). Die Trefferzahlen eines derartig paranormal Begabten folgen der (13, 50%)-Binomialverteilung.
Die folgende Grafik stellt diese beiden Verteilungen dar. Die Zufallsvariable X ist gleich der Trefferzahl eines Tests und P(X=i | H0) bezeichnet die Wahrscheinlichkeit für i Treffer unter der Bedingung der Nullhypothese.
Bei sieben verlangten Treffern ist die Wahrscheinlichkeit eines Übersehfehlers mit 50% genau so groß wie die Power des Tests (hinsichtlich der willkürlich gewählten Hypothese H1). Die Wahrscheinlichkeit eines Vortäuschungsfehlers, das Signifikanzniveau des Tests, ist gleich 0.01 Prozent. Ein paranormal Begabter könnte sich benachteiligt fühlen.
Testergebnisse
Bisher wurde der 1-aus-10-Test der GWUP 37mal durchgeführt. Es gab je zehnmal einen Treffer oder zwei Treffer. Viermal waren drei Treffer und einmal vier Treffer zu verzeichnen. Die restlichen zwölf Tests blieben trefferlos. Diese Häufigkeiten sind mit der Nullhypothese sehr gut vereinbar. Das Testkriterium wurde in keinem Fall erfüllt.
Bei dreizehn Findevorgänge je Test ist der Gesamtumfang der Stichprobe N gleich 481. Die Gesamtzahl k der Treffer ist gleich 46. Die mittlere Trefferzahl je Findevorgang liegt demnach bei knapp 10%, was mit der Nullhypothese gut verträglich ist. Bei dreizehn Versuchen je Test kommt man auf eine „normale“ mittlere Trefferzahl von knapp 1.3. Wenn unter den Kandidaten Psi-Begabte waren, dann muss deren Erfolg durch total Unbegabte mehr als ausgeglichen worden sein.
Bayes-Interpretation des Psi-Tests
Wie sieht es mit den Wahrscheinlichkeiten von Hypothesen aus?
Spaßhalber führen wir den p-Begabten – einen Sonderfall des Psi-Begabten – ein. Der p-Begabte hat im 1-aus-10-Test die mittlere Trefferquote von p. Der 10%-Begabte ist ziemlich normal. Seine Trefferquote entspricht der von Hinz und Kunz, nichts Außergewöhnliches also; er ist die wandelnde Nullhypothese.
Tolerant, wie wir nun einmal sind, stellen wir uns vor, dass es p-Begabte aller Schattierungen geben möge. Sie sind die Elementarereignisse unseres Ereignisraums. Mangels Voreingenommenheit sind für uns alle Begabungen gleichermaßen möglich. Wir gehen vom Indifferenzprinzip aus und nehmen a priori die Zufallsvariable p als gleich verteilt auf dem Intervall von 0 bis 1 an.
Bei einem p größer als 10% sprechen wir von echter Psi-Begabung. Für Werte unterhalb von 10% hat man negativ Psi-Begabte vor sich: Auch bei höchster Anstrengung erzielen sie noch nicht einmal die Zufallstreffer. So einen holt man sich ins Haus, wenn man sicher gehen will, dass der Schatz nicht gefunden wird.
Die Gleichverteilungsannahme ist kaum haltbar. Die bisherigen Testergebnisse ermöglichen uns, etwas mehr über die tatsächliche Verteilung der Psi-Begabung zu erfahren.
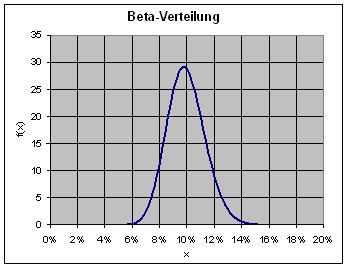
Wir gehen davon aus, dass die Begabungsverteilung durch die Beta-Verteilung mit den Parametern a und b beschrieben werden kann. Zumindest für die A-priori-Schätzung, die Gleichverteilung, ist das möglich. Diese ist nämlich durch die Betaverteilung mit den Werten a = b = 1 gegeben.
Die Bayes-Formel liefert als Lerneffekt aus den Tests eine Betaverteilung zu den Werten a = 1+k = 47 und b = 1+N–k = 436. Wie die Grafik zeigt, konzentriert sich die Psi-Begabung p auf Werte um 10%. Genau das ist nach dem Stand der Wissenschaft auch zu erwarten.
Caveat Emptor: Schlechtere Schätzung durch mehr Daten
Das Paradoxe an der Bayes-Schätzung ist, dass sie gerade für die Fälle nicht funktioniert, für die sie gedacht ist. Die Bayes-Schätzung kann unter Umständen mit jeder weiteren Beobachtung sogar schlechter werden anstatt besser.
Wir betrachten einen Produktionsprozess, der Lose mit unterschiedlichen Fehlerwahrscheinlichkeiten liefert. Diese Fehlerwahrscheinlichkeit p sei also für jedes Los die Realisierung einer Zufallsvariablen aus dem Intervall von 0 bis 1. Die Tests werden für verschiedene Lose durchgeführt.
Die Fehlerwahrscheinlichkeit p sei gleichverteilt, was der Beobachter aber nicht weiß. Er soll mittels Bayesschätzung genau diese Verteilung herausfinden.
Der Beobachter beginnt mit der Gleichverteilung, wie beim obigen Psi-Test. Dass seine Anfangsschätzung bereits die gesuchte Verteilung ist, weiß der Beobachter natürlich nicht.
Überraschung! Eine einfache Simulation zeigt, dass die Schätzung sich mit jedem weiteren Los von der Gleichverteilung wegbewegt. Auch in diesem Fall wird die Verteilungsdichte mit jedem weiteren Test und mit jeder weiteren Beobachtung immer schmaler. Die Verteilung von p wird sich schließlich auf eine kleine Umgebung des Wertes 50% konzentrieren. Jedenfalls hat die Schätzung immer weniger mit der eigentlich zu findenden Gleichverteilung zu tun. Ähnlich gelagerte Fälle zeigen: Mehr Daten führen zu schlechteren Folgerungen (Székely, 1990, S. 126).
Man könnte einwenden, dass man die Bayes-Schätzung nur anwenden darf, wenn der Parameter p eigentlich als konstant anzusehen ist, und dass die Annahme einer Verteilung für p nur unserem Unwissen zuzuschreiben ist, das wir mit jeder Schätzung weiter reduzieren wollen.
Ein derartiger Gewährleistungsausschluss ist jedoch eine Einschränkung, die sich nur von den erzielten Resultaten her und nicht etwa aus dem Verfahren begründen lässt. Dazu Bernhard Rüger (1999, S. 188): „Mit der Angabe einer Verteilung des Parameters ist hier keine Behauptung oder Annahme über die ‚Natur‘ des Parameters verbunden, etwa darüber, ob der Parameter vom Zufall abhängt (eine Zufallsgröße ist) oder eine deterministische Größe darstellt, ja nicht einmal darüber, ob der Parameter überhaupt verschiedene Werte annehmen, also ‚schwanken’ kann, oder einen eindeutig feststehenden, unbekannten Wert besitzt, ein Standpunkt, der innerhalb der Bayes-Inferenz vorherrscht.“
Genau genommen können wir über die Verteilung der p-Begabten bei Psi-Tests nichts erfahren, sollte es solche mit p ungleich 10% überhaupt geben.
Fazit
Testergebnisse lassen keine Rückschlüsse auf die Wahrscheinlichkeitsverteilung des Untersuchungsgegenstands zu. Auch die Bayes-Schätzung hilft nicht wesentlich weiter.
Ratsam ist, sich die einzelnen Psi-Tests anzusehen. Bei den Würzburger Psi-Tests konnte man jeweils mit gutem Grund die behauptete Psi-Fähigkeit verwerfen. Und das sind ziemlich viele Fälle. Das deutet daraufhin, dass wir bezüglich der parapsychologischen Begabung (Psi) die Nullhypothese nicht aufgeben müssen: Vermutlich sind wir ausnahmslos Psi-Unbegabte.
So eindeutig liegt die Sache bei den üblichen statistischen Studien leider nicht. Anders als bei den Psi-Ansprüchen ist die Beleglage pro oder kontra eines Geltungsanspruchs oft ziemlich dünn. Es bleibt die Empfehlung, statistische Studienergebnisse äußerst zurückhaltend zu interpretieren und den Zufall nicht voreilig auszuschließen.
Quellen
Fisz, Marek: Wahrscheinlichkeitsrechnung und mathematische Statistik. Berlin 1976
Novella, Steven: The Skeptics’ Guide to the Universe. 2018
Nuzzo, Regina: Der Fluch des p-Werts. Spektrum der Wissenschaft 9/2014, S. 52-56
Rüger, Bernhard: Test- und Schätztheorie. Band I: Grundlagen. München 1999
Sachs, Lothar: Angewandte Statistik. Anwendung statistischer Methoden. Berlin, Heidelberg 1992
Soehnle, Stefan: Der Psi-Test der GWUP 2004-2014. skeptiker 4/2014 S. 183-188
Székely, Gábor J.: Paradoxa. Klassische und neue Überraschungen aus Wahrscheinlichkeitsrechnung und mathematischer Statistik. Frankfurt am Main 1990
