Corona: Virendynamik im Heimcomputer

Das Corona-Virus hat uns im Griff. Der Griff mag sich, dank der verordneten und überwiegend beherzigten Hygienemaßnahme, etwas lockern. Der Preis dafür ist die massive Einschränkung der Freiheitsrechte durch die Auferlegung von räumlicher Distanzierung, Untersagung von Versammlungen und Großveranstaltungen, Schließung von Geschäften und so weiter.

All das sind „Maßnahmen zur Eindämmung der Ausbreitung des neuartigen Coronavirus SARS-CoV-2“, wie es im Amtsdeutsch heißt. Ab kommendem Montag kommt in Hessen die Maskenpflicht hinzu. So etwas haben wir bisher im Nachkriegsdeutschland weder im Westen noch im Osten erlebt.

Es wird noch eine ganze Weile dauern, wie wir gleich sehen werden. Und auch wenn wir die Sache irgendwann hinter uns bringen, wird irgendwann ein neues Virus auftauchen, und wir stehen vor denselben Fragen und Problemen wie zurzeit: Inwieweit sind die Zwangsmaßnahmen zu rechtfertigen? Unter welchen Bedingungen ist eine Lockerung der Zwangsmaßnahmen angezeigt?

Entscheidungen setzen eine sorgfältige Güterabwägung voraus. Das ist Angelegenheit der Fachleute – Virologen und Epidemiologen – und der Politik. Wir Normalbürger wollen aber schon wissen, „mit welcher Soße wir verspeist werden“. Wir wollen das Ungeheuer zumindest sehen, um einschätzen zu können, welchen Nutzen die Gegenmaßnahmen versprechen.

In den Medien erhält momentan die Dynamik der Virenausbreitung allergrößte Aufmerksamkeit. Jeder kennt inzwischen die Namen der bedeutenden Virologen und Epidemiologen Deutschlands. Sie sagen uns täglich, wie hoch die Reproduktionszahl ist, welche Zuwachsrate gerade gilt und mit welcher Verdoppelungszeit bei den Infektionen wir zu rechnen haben.

Müssen wir Epidemiologie studiert haben, um dieses Zahlenwerk zu verstehen und deren Konsequenzen abschätzen zu können? Nein, ein paar Grundkenntnisse der Populationsdynamik helfen bei der Einordnung und Orientierung und auch bei der Aufdeckung der einen oder anderen Fehleinschätzung, die uns über das Internet erreicht.

Die folgenden Gedanken entwickle ich entlang der Linie meines Kurses Umweltsimulation mit Tabellenkalkulation. Wenn Sie etwas Begeisterung für Mathematik und für die Arbeit mit dem Computer mitbringen, werden Sie Ihr Excel-Programm öffnen und diese Simulationen selbst durchführen wollen.

Die Kenngrößen

Fangen wir mit den Kenngrößen an. Ich will ein paar Annahmen vorausschicken, die in das Design der Kalkulationstabelle einfließen. Zugrunde gelegt wird eine Population des Umfangs K; Ich wähle für die Grafiken K = 80 Mio., das ist in etwa die Anzahl der Einwohner Deutschland. Das ist sozusagen die Kapazität des Virusbehälters. Jeder Erkrankte wird nach fünf Tagen infektiös. Nach weiteren neun Tagen ist er gesund. Der tragische Todesfall bleibt unberücksichtigt. So herzlos es erscheinen mag: In der Dynamik des Virensystems spielt die Todesrate nur eine untergeordnete Rolle; und das hat ja nun auch wieder sein Gutes. (Achtung: Krank nenne ich hier alle, die aktuell infiziert sind, ob sie Symptome zeigen oder nicht. In den Krankenstatistiken erscheinen nur diejenigen, die  Symptome zeigen.)

Beim Ausbruch der Krankheit, also wenn kaum einer infiziert ist, steckt jeder Infizierte eine gewisse Anzahl von Mitbürgern an. Das ist die Basisreproduktionszahl R₀. Man spricht beim Corona-Virus von Werten so um die drei. Je mehr Leute immun sind, umso weniger Opfer findet das Virus. Die Reproduktionszahl R ändert sich also mit der Zeit. Anfangs ist R = R₀.

Eine weitere Kenngröße ist die relative Infektionsrate  r. Sie sagt uns, welchen Anteil die Zahl der Neuinfizierten eines Tages an der Gesamtzahl der momentan Infektiösen hat. Da voraussetzungsgemäß jeder Erkrankte neun Tage lang infektiös ist, ist die Zuwachsrate ein Neuntel der Reproduktionszahl, also: r = R/9. Bei einer Reproduktionszahl von R = 1,8 ist die relative Infektionsrate r also gleich 20%.

Die Infektionsrate ist anfänglich gleich r₀ = R₀/9. Mit zunehmender Zahl N von Leuten, die sich bereits infiziert haben und zum Teil auch wieder gesund sind, reduziert sich die Zahl derer, die überhaupt noch infiziert werden können, sie ist gleich K–N. Dementsprechend setzen wir die aktuell wirksame Infektionsrate auf r = r₀∙(K–N)/K.

Die Kalkulationstabelle

In der Tabelle (Arbeitsblatt „Dynamik“) steht jede Zeile für einen Tag. Sie hat sechs Spalten. In der ersten werden die Tage durchnummeriert (Variable i), in der zweiten Spalte steht die Zahl der an dem jeweiligen Tag neu Infizierten. Für den Tag null ist diese Zahl vorgebbar. Dann kommt die Spalte mit der Zahl X_i derer, die an diesem Tag infiziert sind, gefolgt von der Gesamtzahl N_i der bisher insgesamt Infizierten. In den letzten beiden Spalten stehen die jeweilige Reproduktionszahl R_i und die Infektionsrate r_i.

Die Spalte der neu Infizierten ist die eigentlich interessante. Für den Tag null (i = 0) wird ein Anfangswert eingetragen, beispielsweise der Wert eins für nur einen anfangs Infizierten. In jeder anderen Zeile i steht die Anzahl der zum Zeitpunkt i-1 infektiösen Personen, das ist die Summe aller Neuinfizierten der Tage von i-14 bis i-6, soweit diese vorhanden, multipliziert mit der für den Vortag gültigen Infektionsrate r_i-1.  Damit hat man die Anzahl der am Tag i neu Infizierten.

Die Formeln der anderen Spalten sind einfach: X_i enthält die Zahl der momentan infizierten Personen; diese ist gleich der Summe aller in den letzten vierzehn Tagen neu infizierten Personen. N_i enthält die Summe sämtlicher Personen, die bisher infiziert waren oder infiziert sind. Die aktuell wirksame Infektionsrate ergibt sich aus der obigen Formel. Die Reproduktionszahl ist das Neunfache dieses Wertes.

Ergebnisse

Das erste Bild ist Ergebnis eines Simulationslaufs mit der Basisreproduktionszahl 4,5.  Es fängt harmlos an. Ab dem fünfzigsten Tag ist das exponentielle Wachstum nicht zu übersehen. Der Kurve lassen sich jetzt auch die Zeiten bis zur jeweiligen Verdopplung der Infizierten entnehmen. Am hundertsten Tag etwa erreicht die Zahl der Infizierten den Höchstwert. Die Zahl der aktuell Infizierten stagniert und geht dann zurück. Dementsprechend sinkt die Reproduktionszahl auf Werte unter eins und nähert sich dem Wert null. Die Bevölkerung ist nahezu komplett durchseucht. Fast jeder war einmal infiziert.

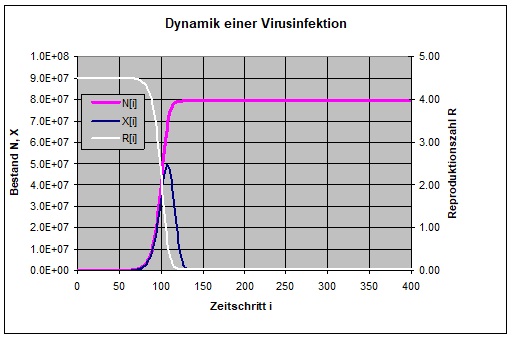
Bei so einem Verlauf wird das Gesundheitssystem kurzzeitig stark belastet: Zur Hochzeit der Pandemie ist mehr als die Hälfte der Bevölkerung krank.

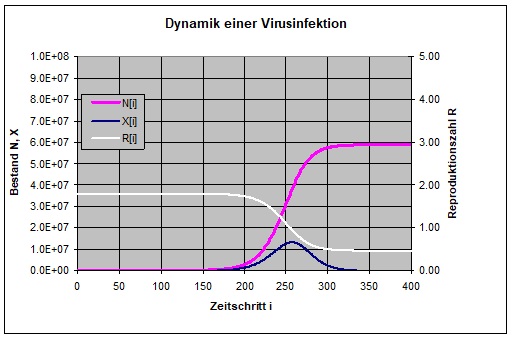
Im folgenden Bild wird deutlich, was eine Verringerung der Basisreproduktionszahl durch strengere Eindämmungsmaßnahmen bewirkt. Die Simulation wurde mit dem Wert 1,8 durchgeführt.  Die Spitzenbelastung ist jetzt gegenüber dem ersten Simulationslauf um fast den Faktor  fünf reduziert. Die Belastung ist insgesamt zwar geringer, aber es dauert wesentlich länger, bis die Pandemie überwunden ist. Bemerkenswert ist, dass die Reproduktionszahl gar nicht auf null absinken muss, um die Pandemie zu überwinden. Hier liegt sie schließlich knapp über 50%. Die Durchseuchung der Gesellschaft ist nicht vollständig; sie  liegt schließlich bei 74%.

Zum Schluss

Der österreichische Bundeskanzler Sebastian Kurz sagte auf einer Pressekonferenz: „Der Replikationsfaktor muss unter 1 sinken und mittelfristig in Richtung 0 verlaufen.“ Ulrich Berger widerspricht in seinem Ökonomieblog auf derStandard.de („Epidemiologie im Bundeskanzleramt mit drei Fragezeichen“, 1.4.2020): „In Wuhan etwa wurde laut dem Expertenpapier durch starke Abschottung sogar eine Reproduktionszahl von 0,32 erreicht. Ein R₀ nahe bei 0, wie es Sebastian Kurz im Sinn zu haben schien, wäre dagegen eine gefährliche Drohung. Es würde nämlich eine extreme weitere Verschärfung der bisherigen Maßnahmen erfordern, deutlich über jene in Wuhan hinaus, bis hin zur fast völligen Isolation aller Einwohner des Landes. Zum Glück ist das nicht notwendig.“

Mittels Tabellenkalkulation haben wir den Hintergrund von Ulrich Bergers Widerspruch ausgeleuchtet. Damit sind wir nicht zu Experten für Epidemiologie geworden. Wir haben nur das gemacht, was dem Bürger zusteht: einmal genauer hinsehen auf das, was die Politiker und Fachleute so treiben.

Und noch etwas: Um die obigen Schreckensszenarien zu vermeiden, versuchen wir zurzeit die Basisreproduktionsrate unter den Wert eins zu drücken. Die Phase exponentiellen Wachstums wird so vermieden, aber auch die der Herdenimmunintät; Ziel ist, den Krankenstand so zu senken, dass Einzelfallverfolgung wieder möglich wird. Mit derart lokal begrenzten Eindämmungsmaßnahmen ließe sich die Zeit bis zu einer dann hoffentlich möglichen Corona-Impfaktion leidlich überbrücken. Mai Thi hat dazu mehr zu sagen.