Proben mit Stich: Wie „farbtreu“ sind Umfrageergebnisse?

Undefinierte Grundgesamtheit und verzerrte Stichproben

Leserbeteiligung fördert die Auflage. Und am einfachsten gelingt das mit TED-Umfragen. TED steht für Teledialog und wurde erstmals in Fernsehshows zur Einbindung der Zuschauer genutzt. Inzwischen grassiert dieser Umfragebazillus. Neulich wurde ich von meiner Tageszeitung aufgefordert, meine Meinung darüber abzugeben, ob Autos mit Zündsperren für Alkoholsünder (Alkolocks) ausgestattet werden sollen oder nicht. Der Abstimmungsakt erfordert nur, je nach Antwort eine entsprechende Telefonnummer zu wählen.

Inzwischen kenne ich das Ergebnis dieser Telefonumfrage: 65,9 % sind für die Zündsperren, 34,1 % sind dagegen (Fuldaer Zeitung vom 23.4.2011).

Hoppla! Von wem ist hier überhaupt die Rede? Von den Osthessen, von den Fuldaern, von den Lesern der Zeitung? Nein: hier ist nur die Rede von denen, die an der Telefonumfrage teilgenommen haben. Und wer diese Leute sind, kann niemand sagen, auch die Redaktion nicht. Ich weiß jetzt nur, dass von denen, die angerufen haben, 65,9 % für die Zündsperren sind und der Rest dagegen. Die Teilnehmer an der Umfrage rekrutieren sich selbst: Das Interesse an einer bestimmten Antwort erzeugt den Drang zur Teilnahme. Und ich weiß nicht, ob eher der Zündsperren-Befürworter oder aber dessen Gegner genügend Blutdruck entwickelt, den man braucht, um zum Telefonhörer zu greifen. Es bleibt die ernüchternde Erkenntnis, dass die Zeitung eine vollkommen wertlose Nachricht geboten hat.

Ergebnis einer Online-Umfrage

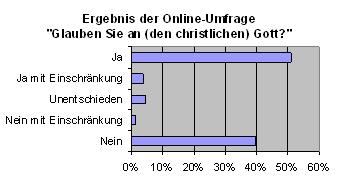
Auch Web-Seitenanbieter versuchen mit ähnlich gearteten Umfragen ihr Angebot interessanter zu machen. Auf einer Atheisten-Seite wird um Abstimmung gebeten zur Frage: „Glauben Sie an (den christlichen) Gott?“ Diese Abstimmung läuft schon seit einigen Jahren und hat inzwischen 21704 Teilnehmer gefunden. Ich habe das Ergebnis in der nebenstehenden Grafik komprimiert dargestellt (Stand: 21.4.2011).

Hier haben wir dasselbe Problem wie bei den Alkolocks: Der unkritische Leser sieht in dieser Grafik ein Abbild der Glaubensneigung der Bevölkerung – was immer er unter „Bevölkerung“ verstehen mag. Der Nachdenkliche schränkt den Kreis auf die Besucher der Atheisten-Seite ein. Aber auch das ist eine noch viel zu kühne Verallgemeinerung: Die Statistik sagt nur etwas über die Teilnehmer an der Abstimmung aus. Und über diesen Personenkreis wissen wir so gut wie nichts.

An der Abstimmung können normale Besucher der Seite teilgenommen haben. Aber es kann auch sein, dass irgendwelche religiösen oder atheistischen Zirkel eine Abstimmungsaktion organisiert haben. Wer weiß?

Aber eins ist doch interessant: Die Gleichgültigen sind zusammen mit den Wachsweichen klar in der Minderheit. Um sich zur Teilnahme aufraffen zu können, braucht man schon etwas Enthusiasmus. Der ist bei den Gläubigen offenbar vorhanden, und die wahren Atheisten stehen ihnen kaum nach. Das Ergebnis der Abstimmung läuft auf eine Tautologie hinaus: Gläubige glauben, Ungläubige nicht. Das ist aber auch schon alles.

Die hier beschriebenen Umfragen müssen scheitern, weil sie gegen grundlegende Voraussetzungen des statistischen Schließens verstoßen. Die erste Voraussetzung besagt, dass die Grundgesamtheit – also die Population, über die etwas ausgesagt werden soll – klar definiert sein muss. Und die zweite Forderung ist, dass das Ziehen einer Stichprobe aus dieser Grundgesamtheit nach dem Zufallsprinzip zu erfolgen hat. Die Stichprobe soll ja für die Grundgesamtheit repräsentativ sein. Selbstrekrutierte Stichproben erfüllen diese Forderungen ganz gewiss nicht. Sie sind fast notgedrungen verzerrt.

Auch seriös angelegte Umfragen mit gut definierter Grundgesamtheit und gut geplanter Stichprobenbildung können das Problem der verzerrten Stichprobe nicht ganz vermeiden. Ein Hauptgrund sind die Fälle von Antwortverweigerung (Non-response). In den Nachrichten aus dem Statistischen Bundesamt (METHODEN – VERFAHREN – ENTWICKLUNGEN, Ausgabe 2/2004) wird berichtet, dass bei Auswahlverfahren für Telefonstichproben mit einer Antwortverweigerungen von „über 50% bei Erstbefragungen und rund 10% bei Folgebefragungen“ gerechnet werden muss. Die Antwortverweigerung bildet ein großes Einfallstor für Verzerrungen, das sich kaum schließen lässt.

Da wir gerade bei Glaubensfragen sind: Auch der Religionsmonitor der Bertelsmann-Stiftung muss sich mit dem Problem der Antwortverweigerung herumschlagen. Und bei solchen weltanschaulichen Fragen könnte das besonders hart werden.

Ein Beispiel aus der Konsumforschung

Am 1. September 1999 berichtete die Fuldaer Zeitung über ein Gutachten zur Konsumforschung: „Interessant … ist …, dass über die Hälfte der Passanten täglich oder mehrmals pro Woche Fuldas Innenstadt aufsuchen. 25,8 Prozent kommen einmal pro Woche oder mindestens 14-täglich. Demnach kann davon ausgegangen werden, dass die Innenstadt ein umfangreiches Angebot für die Kunden bereithält.“

Offenbar ist beabsichtigt, die Tatsache, dass immerhin 50 Prozent der angetroffenen Passanten täglich und nur 25 Prozent wöchentlich kommen, als Zeichen der Attraktivität Fuldas hinzustellen. Wie lässt sich das begründen?

Zuerst ist nach der Grundgesamtheit zu fragen, die es zu beurteilen gilt. Aber darüber sagt das Gutachten nichts aus: Befragt wird nur, wer da ist. Jemand, der sehr selten oder gar nicht nach Fulda kommt, wird durch die Stichprobe nicht vertreten.

Also verzichten wir darauf, die Grundgesamtheit zu präzisieren und fragen nur, in welchem Verhältnis die Anzahl der Vielbesucher (täglich) zur Anzahl der Wenigbesucher (wöchentlich) steht. In der Stichprobe beträgt dieses Verhältnis etwa 50/25, also 2:1. Aber dieses Verhältnis interessiert uns eigentlich nicht. Wir wollen wissen, wie dieses Verhältnis in der imaginären Grundgesamtheit (Menschen des Landkreises oder der Region) ist.

Jeder befragte Besucher vertritt eine Anzahl von Personen der Grundgesamtheit. Die Wenigbesucher mögen sich auf die sechs Arbeitstage einer Woche gleichmäßig verteilen. Jeder befragte Wenigbesucher vertritt also sechsmal mehr Personen der Grundgesamtheit als jeder Vielbesucher. Wenn man das Verhältnis der Viel- zu den Wenigbesuchern auf die Grundgesamtheit umrechnet, kommt der Faktor sechs ins Spiel: Aus dem Verhältnis 2:1 wird das Verhältnis 2:6 oder 1:3. Also: Die Zahl der Wenigbesucher übertrifft die der Vielbesucher um das Dreifache.

In diesem Fall haben wir — mittels einer gewagten Annahme — aus einer selbstrekrutierten Stichprobe tatsächlich etwas über die Grundgesamtheit erfahren. Das ist zwar nicht viel, aber immerhin.

Ich habe großes Vertrauen in die interpretatorischen Fähigkeiten der Konsumforscher. Auch mit diesen Zahlen hätten sie die von ihnen gewünschte Aussage gewiss problemlos untermauern können.

Erhöht Ausweichen die Kollisionsgefahr?

Sogar angesehene Unfallforscher sind vor den Tücken verzerrter Stichproben nicht gefeit. Ein zentraler Abschnitt des berühmten Buches „Normale Katastrophen“ von Charles Perrow (1987) enthält diesen Text: „Die meisten Schiffskollisionen, von denen ich geeignete Unfallberichte ausfindig machen konnte, ereigneten sich zwischen Schiffen, die sich zunächst nicht auf Kollisionskurs befanden, sondern erst zusammenstießen, nachdem mindestens einer der Kapitäne das andere Schiff entdeckt und daraufhin seinen Kurs geändert hatte… Was um alles in der Welt bringt die Kapitäne riesiger Schiffe dazu, Kursänderungen in letzter Minute anzuordnen, die dann überhaupt erst eine Kollision verursachen?“

Perrow folgert aus den Daten, dass Ausweichen die Kollisionsgefahr erhöht. Dabei zieht er nur die Fälle in Betracht, in denen es schief gelaufen ist. Die Lage lässt sich aber nur dann richtig beurteilen, wenn der Blick über die verzerrte Stichprobe hinausgeht — hin zu einer passend definierten Grundgesamtheit. Was nämlich nicht in seiner Rechnung erscheint, sind die Beinahekollisionen, bei denen die Ausweichmanöver erfolgreich waren oder ohne Nachteil unterblieben sind.

Versuchen Sie doch einmal, durch Blickfelderweiterung zu einer besseren Interpretation der Daten zu kommen. Meinen Versuch finden Sie im Aufsatz „Denkfallen — Klug irren will gelernt sein“.