Im ersten Teil von „Denksport am Rande des Wahnsinns“ ging es um Mathematik in der Schule, speziell um die vollständige Induktion und um Optimierungsaufgaben. Im zweiten Teil suche ich nach Antworten auf die Frage, was es mit dem Grundstoff der Mathematik, mit den Zahlen, auf sich hat.
Die Welt der Zahlen
Die größte Zahl
Der Name der größten Zahl stammt von einem Kind. Sein Onkel, ein Mathematiker, hatte die Zahl an die Tafel geschrieben und das Kind meinte, dass das wie ein Googol aussehe. Unter Beteiligung von etwas Legasthenie wurde daraus später der Name der heute beliebtesten Suchmaschine im Internet. Wen die ganze Geschichte interessiert, der möge diese Suchmaschine bemühen oder in „Eine kleine Geschichte der Unendlichkeit“ von Brian Clegg nachsehen (2015, S. 57).
Im Alltagsleben kommt man immer mit deutlich kleineren Zahlen aus. Dem Googol kommt mit Fug und Recht das Prädikat zu, die größte Zahl zu sein. Und wie groß ist nun ein solches Googol? Jedenfalls ist es größer als die Anzahl der Atome im Universum. Ein Googol ist eine Eins gefolgt von einhundert Nullen: 10.000.000.000.000.000.000.000.000.000.000.000.
000.000.000.000.000.000.000.000.000.000.000.
000.000.000.000.000.000.000.000.000.000.000
Linien bestehen aus Punkten, oder?
Jede Strecke besteht aus Punkten. Soweit herrscht Einvernehmen. Aber: Wie viele sind es? Jetzt ist es mit der Einigkeit vorbei. Nähern wir uns der Angelegenheit ganz vorsichtig, indem wir mit dem Vergleichen beginnen,
Wir sprechen beim Umfang oder bei der Größe von Mengen besser von Mächtigkeit, wenigstens sobald wir den Bereich der endlichen Mengen verlassen. Zwei Mengen haben dieselbe Mächtigkeit, wenn es eine Eins-zu-eins-Abbildung zwischen ihren Elementen gibt. Haben die Mengen nur endlich viele Elemente, dann ist die Mächtigkeit gleich der Anzahl dieser Elemente. Die Menge {A, B, C} hat die Mächtigkeit 3, genauso die Menge aus einem Apfel, einer Birne und einer Zitrone. Nimmt man zu einer solchen endlichen Menge ein weiteres Element hinzu, erhöht sich deren Mächtigkeit um eins.
Nehmen wir die Menge der natürlichen Zahlen, dann kann man ein weiteres Element hinzufügen und es entsteht eine Menge derselben Mächtigkeit: Nach wie vor lassen sich alle Elemente abzählen, zum Beispiel so: 1 ist die Nummer des hinzugefügten Elements, 2 die Nummer für die 1, 3 die Nummer für die 2 usw. Es gibt also eine Eins-zu-eins-Abbildung zwischen der Menge der natürlichen Zahlen und der neu gebildeten Menge mit einem zusätzlichen Element.
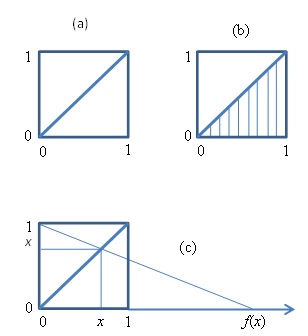Wir vergleichen zwei Strecken. Nehmen wir eine Seite des Einheitsquadrats und vergleichen diese mit der Diagonalen, Bild (a). Es gibt eine Eins-zu-eins-Abbildung von allen Punkten der einen Strecke zu denen der anderen, wie in Bild (b) angedeutet. Die Punktmengen der Strecken haben folglich dieselbe Mächtigkeit, obwohl die Strecken offensichtlich ungleich lang sind (Lietzmann, 1962, S. 120). Der Wahnsinn schimmert auf.
Bild (c) zeigt, dass die Menge der Punkte von 0 bis 1 dieselbe Mächtigkeit hat, wie die Menge der Punkte von 0 bis unendlich. Eine Funktion, die jedem Zahlenwert des Intervalls von 0 bis 1 umkehrbar eindeutig einen Wert des positiven Zahlenstrahls zuordnet, ist f(x) = x/(1-x).
Die Punkte zeigen hier ihre unheimliche Seite. Sie sind unendlich klein, sie entziehen sich der Anschauung; wir nennen sie Infinitesimale. Es ist kein Wunder, dass man sie über Jahrhunderte hinweg möglichst ignorierte und schließlich sogar verbot, sich mit ihnen in der Lehre zu befassen.
Das Infinitesimale, das Unteilbare, das Atom hat die Ausdehnung null. Und aus solchen Atomen lässt sich kein Gegenstand der realen Welt zusammensetzen. Der Traum von der Harmonie der Welt, die Vorstellung, dass alles Zahl sei, ist damit geplatzt. Das Unteilbare und mit ihm der Atomismus mussten aus der Wissenschaft verbannt werden.
Genaugenommen spricht man vom Infinitesimalen erst dann, wenn das unendlich Kleine als Grenzelement einer handhabbaren endlichen Näherung erscheint. In der Anfangszeit genügten diese Näherungen nicht den Anforderung der mathematischen Strenge. Der Bannspruch war also nicht ganz grundlos.
Die Geometrie hingegen kommt mit dem Unteilbaren zurecht. Ihr Erfolg beruht darauf, dass sie auf Definitionen für ihre elementaren Objekte wie Punkt und Gerade verzichtet. Stattdessen zeigt sie nur, was man mit ihnen alles anstellen kann (Denkfalle Realität). Bei diesem Stand des Wissens scheint die Geometrie für die Welterklärung besser geeignet zu sein als die Welt der Zahlen.
Die Ächtung der Infinitesimalen dauerte bis in die Neuzeit an. Gegen Ende der Renaissance-Zeit kam unter dem Einfluss der Jesuiten die Entwicklung der Mathematik in Italien, bis dahin vorangetrieben durch Galileo Galilei, Bonaventura Cavalieri und Evangelista Torricelli, zum Erliegen (Alexander, 2014, S. 17 ff.). Die Weiterentwicklung verlagerte sich nach Norden: Isaac Newton und Gottfried Wilhelm Leibniz vollendeten das Programm des Unteilbaren und stellten die Lehre mit Beginn des Barock auf eine gesunde Basis. Sie schufen mit einer Verzögerung von einem halben Jahrhundert aus den Vorarbeiten der Italiener die Infinitesimalrechnung.
Ohne Infinitesimalrechnung hätten wir keine Theorie des Elektromagnetismus und keine der Hydrodynamik. Effiziente Turbinen und Motoren, Rundfunk, Telefonie, Flugzeuge oder Automobile wären außer Sichtweite. Es gäbe keine schlanken Brückenkonstruktionen und keine kühnen Hochhäuser mit ihren Aufzügen. Andersherum gesehen: Unser ganzes modernes Leben ist durchdrungen von dieser neuen Mathematik.
Wie wär’s mit ein wenig Denksport, der uns den alltäglichen Wahnsinn ein wenig vertraut macht. Beweisen Sie den folgenden
Satz 1: Die Vereinigung zweier abzählbarer Mengen ist abzählbar.
Rationale Zahlen
Wir gehen jetzt noch einen Schritt weiter und bilden die Vereinigung von abzählbar vielen abzählbaren Mengen A, B, C, …, wobei A = {A1, A2, A3, …}, B = {B1, B2, B3, …}, C = {C1, C2, C3, …} und so weiter. Ich ordne die Elemente der Vereinigungsmenge dreiecksförmig an, so dass sich durch zeilenweises Durchnummerieren der Elemente eine Abzählung aller Elemente der Vereinigungsmenge ergibt:
A1
B1 A2
C1 B2 A3
D1 C2 B3 A4
…
Hintereinander geschrieben: A1 B1 A2 C1 B2 A3 D1 C2 B3 A4 …
Daraus folgt der
Satz 2: Die Vereinigung einer abzählbaren Menge von abzählbaren Mengen ist abzählbar.
Der Beweis zum folgenden Satz 3 ist nach diesen Vorbereitungen eine ziemlich leichte Denksportaufgabe.
Satz 3: Die Menge der rationalen Zahlen, das sind die Brüche ganzer Zahlen, ist abzählbar.
Wen interessiert, wie man systematisch alle rationalen Zahlen erzeugen kann, und zwar ohne dass sie mehrfach auftreten, wie beispielsweise 1/2, 2/4, 3/6, usw., dem empfehle ich den Aufsatz „Rationale Zahlen“ von Christoph Pöppe (2021).
In jedem noch so kleinen Fitzelchen der Zahlengerade finden wir unendlich viele rationale Zahlen. Die Menge von dermaßen dicht liegenden rationalen Zahlen soll genau so mächtig sein, wie die natürlichen Zahlen, die auf der Zahlengeraden locker verteilt sind? Ja, so ist es. Finden wir uns damit ab!
Mächtig, aber nicht groß
Auch kleinste Streckenschnipsel haben dieselbe Mächtigkeit wie eine unendlich ausgedehnte Gerade. Davon konnten wir uns überzeugen. Also: Mächtig ist nicht gleichbedeutend mit groß.
Da die rationalen Zahlen auf der Zahlengeraden dicht liegen, sollte sich damit jede Strecke ausmessen lassen. Die rationalen Zahlen sind offenbar alles, was man zum Messen braucht. Die Ernüchterung folgt, wenn man versucht, der Diagonale des Einheitsquadrats eine Länge zuzumessen, Bild (a). Wir werden sehen, dass diese Länge keine rationale Zahl sein kann.
Wir führen einen indirekten Beweis und gehen vom Gegenteil aus, nämlich dass die Länge der Diagonale gleich m/n ist, mit zwei natürlichen Zahlen m und n. Wir dürfen gefahrlos voraussetzen, dass wenigstens eine der Zahlen ungerade ist.
Nach dem Satz des Pythagoras müsste (m/n)2 = 2 sein. Zur Herleitung des Widerspruchs können Sie den folgenden Satz verwenden. Der Beweis bietet sich als kleine Denksportaufgabe an.
Satz 4: Das Quadrat einer Zahl ist genau dann ungerade, wenn die Zahl selbst ungerade ist.
Der Rest des Widerspruchsbeweises ist nun kein Hexenwerk mehr.
Unendlich und darüber hinaus
Um auch das Wurzelziehen und weitere Operationen im Zahlenbereich einschränkungslos durchführen zu können, müssen wir ihn erweitern. Wir nehmen die unendlichen Dezimalbrüche dazu, das sind Darstellungen sämtlicher reellen Zahlen.
Zwei Sonderfälle gibt es: die rationalen Zahlen, deren Nenner eine Zehnerpotenz ist: 1, 10, 100 usw. Das sind die abbrechenden Dezimalbrüche. Sie machen komischerweise, wenn wir abzählen wollen, die meisten Schwierigkeiten, denn sie erlauben zwei Darstellungen: einmal als abbrechenden Dezimalbruch wie beispielsweise 5,38, aber auch als unendlichen Dezimalbruch, der entsteht, wenn man die letzte Stelle um eins erniedrigt und dann lauter Neunen anhängt, am Beispiel: 5,379999… Und dann gibt es noch die Dezimalzahlen für die Brüche. Die erkennt man daran, dass sie in eine periodische Folge übergehen: 13/11 = 1.18181818…
Eine der Grundtatsachen der Mengenlehre ist, dass die reellen Zahlen tatsächlich nicht abzählbar sind, ihre Mächtigkeit geht über die der natürlichen Zahlen und die der rationalen Zahlen deutlich hinaus. Eine offene Frage der Mathematik ist, ob es eine Teilmenge der reellen Zahlen gibt, deren Mächtigkeit größer als die der Menge der natürlichen und kleiner als die der Menge der reellen Zahlen ist. Davon war im Hoppla!-Blog bereits die Rede: Wie real ist unendlich?
Wieviel Mathematik steckt in der Welt?
Unser Wissen über die Welt ist in Theorien enthalten, von denen wir annehmen, dass sie immer und überall gelten. Sie beinhalten Regelmäßigkeiten, die wir in den Erscheinungen beobachten können. Sie sind überwiegend in der Sprache der Mathematik verfasst. Musterbeispiel ist das newtonsche Gesetz: Kraft gleich Masse mal Beschleunigung – in mathematiküblicher Kurzform: F = m×a.
Bereits Galileo Galilei soll gesagt haben, dass die Naturgesetze in der Sprache der Mathematik verfasst worden seien. Diesen Gedanken greift Eugene Wigner auf, wenn er über die unbegreifliche Effektivität der Mathematik in den Naturwissenschaften sinniert (1960).
Realisten und Naturalisten liegen genau auf dieser Linie. Sie sprechen davon, dass es nur eine Welt gebe, „dass also das Objekt unserer Erkenntnis, die Welt, einmalig und eindeutig bestimmt sei“. Sie setzen ferner voraus, „dass wir diese Welt erkennen können“. (Vollmer, 2003, S. 15)
Wenn Gerhard Vollmer schreibt „Die Forschung konvergiert, weil es reale Strukturen gibt, die wir entdecken können und tatsächlich allmählich entdecken“ (S. 43), dann kommt er der Vorstellung sehr nahe, dass die Forscher dabei sind, das Buch der Natur Seite für Seite zu entziffern – Irrtümer inbegriffen. Da ihre Sprache die der Mathematik ist, heißt das: sie nehmen an, dass das Buch der Natur in der Sprache der Mathematik verfasst ist, und dass sie beim Entziffern immer mehr dieser Mathematik zu begreifen lernen. Das ist idealistisches Denken wie einst bei Platon.
Warum aber kommen dann so viele Mathematik-Analphabeten gut durchs Leben? Einfach weil Mathematik in den meisten Lebensbereichen so gut wie keine Rolle spielt: Rechtswesen und Kunst kommen weitgehend ohne mathematische Theorien aus. Eine der wichtigsten Fragen, nämlich die nach der Natur des Ich, verweigert sich beharrlich einer wissenschaftlichen Lösung. Die ausgiebige Diskussion zum Thema Das fünfte Welträtsel: Bewusstsein, die im Scilog-Blog Menschen-Bilder ihre Fortsetzung fand, zeugt davon. Da hilft auch die höhere Mathematik nicht weiter.
Richard Hamming schreibt, dass wir im Grunde immer nur das sehen, wonach wir suchen (1980). Haben wir die mathematischen Instrumente, dann suche wir nach Anwendungen dafür; und siehe da: ein neues Wissenschaftsfeld entsteht. Es ist keineswegs unbegreiflich, wenn die Mathematik dort gut funktioniert. Davon sind wir gebannt und halten es für die gesamte Welt.
Das am schwersten wiegende Argument gegen so etwas wie das Welt-Mathematikbuch scheint mir zu sein, dass das Unendlich, das der Mathematik ihren Glanz verschafft, in der wirklichen Wirklichkeit keinen Platz hat. Wenn wir meinen, dem Unendlich zu begegnen, dann hat das immer einen Anflug von Wahnsinn. Jedenfalls verursacht es Unbehagen und man wäre es gern wieder los.
Das leichte Schwindelgefühl beim virtuellen Unendlich zwischen den Spiegeln lässt sich noch gut aushalten. Aber die Betrachtung des Ich, das sich selbst betrachtet wie es sich selbst betrachtet: Das geht denn doch zu weit. Der Philosoph fürchtet derartige infinite Regresse. Sie sagen ihm, dass er dabei ist, verbotenes Terrain zu betreten.
Von der Unendlichkeit von Zeit und Raum und vom unendlich Kleinen handeln die ersten beiden Antinomien des Immanuel Kant. Er zeigt, dass sich solche Antinomien nicht mittels Vernunft auflösen lassen und dass man besser die Finger davon lässt.
Das Unendlich hat in der Philosophie nicht den besten Ruf, wie man sieht. Wenn es um das Bewusstsein geht, scheint der beste Weg aus der Bredouille zu sein, das Ich ganz zu eliminieren. Aber dieses Thema hatten wir schon im Artikel Wie real ist unendlich?
Literatur
Vollmer, Gerhard: Wieso können wir die Welt erkennen? Hirzel, Stuttgart 2003
Wigner, Eugene: The Unreasonable Effectiveness of Mathematics in the Natural Sciences. Communications in Pure and Applied Mathematics, Vol. 13, No. I (February 1960).
Hamming, Richard W.: The Unreasonable Effectiveness of Mathematics. The American Mathematical Monthly, Vol. 87, No. 2 (February 1980), pp. 81-90.
Lietzmann, Walther: Wo steckt der Fehler? Mathematische Trugschlüsse und Warnzeichen. Teubner, Stuttgart 1935/1962
Clegg, Brian: Eine kleine Geschichte der Unendlichkeit. Rowohlt, Reinbek 2015
Pöppe, Christoph: Mathematische Unterhaltungen. Rationale Zahlen. Spektrum der Wissenschaft 5/2021, S. 82-86
Alexander, Amir: Infinitesimal. How a Dangerous Mathematical Theory Shaped the Modern World. Scientific American, New York 2014
Ich finde ihren Artikel sehr gelungen!
Ein anderes schönes (praktisches) Beispiel sind hier z.B. Polarkoordinaten. Ich kann einen Kreis mit Radius R in unendlich viele Segmente mit unendlich kleinen Teilwinkel unterteilen. Die unendlich kleine Bogenlänge jedes Segmentes ist um R größer als der Teilwinkel. Wie in Ihrem Beispiel steckt zwischen Winkel und Bogenlänge eine Abbildungsfunktion.
Hier ist es anschlaulich, dass ein unendlich kleiner Winkel was anderes ist, als die dazugehörige unendlich kleine Bogenlänge. (Allein schon durch die Einheiten)
Weiter kommt man bei vielen physikalischen Fragestellungen durch einen Grenzwertprozess zur Infinitisimalrechnung. Das macht das Verständnis meiner Meinung nach häufig einfacher.
btw, ich habe eigentlich irgendwo im Artikel mit Hilberts Hotel gerechnet :-)
An Hilberts Hotel habe ich gedacht und auch daran, dass der Rätselfreund selber drauf kommt. Wie geschehen :-)
Dass die Jesuiten die Entwicklung der italienischen Mathematik bremsten, war mir nicht präsent. Dank für diesen Hinweis.
Mir ist aufgefallen, dass die Binärbrüche 0,011111… mit wachsender Zahl der hinzugefügten Einsen nach 0,1 (=1/2) konvergieren. Die obige Eigenschaft gilt also nicht nur im Dezimalsystem.
Schöne Grüße
Wo Schatten ist, da ist auch Licht. Die Jesuiten galten im Fach Mathematik als Lehrmeister Europas. Die Kalenderreform von 1582 war ihr Werk. Es ist sicher auch diesem guten Ruf zuzuschreiben, dass ihre Ablehnung des Infinitesimalen so schwerwiegende Folgen hatte.
Tja, wirklich ärgerlich. Die Mathematik stellt Hilfsmittel bereit, weil sie praktisch dazu gezwungen wird. Man will die Diagonale im Quadrat durch Zahlen ausdrücken, und das Verhältnis von Kreisumfang zu -durchmesser, man will den Treffpunkt von Achilles und der Schildkröte berechnen können, und die Lösungen von Newtons Differenzialgleichungen natürlich auch. Und dann entwickeln die Hilfsmittel ihr Eigenleben, türmen Unendlichkeiten auf Unendlichkeiten, erklären die rationalen Zahlen für einen vernachlässigbaren Anteil aller reellen Zahlen, und am Ende kommt so etwas wie das Banach-Tarski-Paradox, auf das man – ehrlich gesagt – prima hätte verzichten können.
Soll man deswegen die Hilfsmittel wegschmeißen? Bloß nicht!! Siehe oben. Gibt es bessere Hilfsmittel, die dasselbe leisten? Sieht nicht so aus. Also werden wir mit dem Unendlichen und dem ganzen zugehörigen, mühsam in Grenzen gehaltenen Ärger leben müssen.
Naturalisten „nehmen an, dass das Buch der Natur in der Sprache der Mathematik verfasst ist, und dass sie beim Entziffern immer mehr dieser Mathematik zu begreifen lernen. Das ist idealistisches Denken wie einst bei Platon.“
Hierbei handelt es sich um das sog. Anwendungsproblem der Mathematik in den empirischen Wissenschaften, das Vollmer im oben zitierten Buch auf den Seiten 122-143 behandelt. Dort ist allerdings nicht vom „Buch der Natur“ oder von platonischen Ideen die Rede, sondern z.B. von Mathematik als Strukturwissenschaft, Isomorphie und der (meta)mathematischen Modelltheorie. Das Kapitel lässt sich nicht in 2-3 Sätzen zusammenfassen, da es recht komprimiert geschrieben ist.
Mein Hinweis auf Platon passt schon. Das zentrale Missverständnis der Naturalisten ist jedoch, dass sie das Wahrgenommene für die Welt halten. Wahrnehmung ist erwartungsgetrieben: „Wir sehen nur, was wir glauben.“ (Klüger irren, 2020, S. 8)
„Wir sehen nur, was wir glauben.“
Ich lese das als Tautologie: „Ich sehe, was ich sehe.“ Dem kann ich zustimmen.
Wortspiele sind scheint’s nicht jedermanns Sache, lieber Manfred.
„Wir glauben zu sehen“, lässt sich kurz als „Wir sehen“ schreiben. „Ich sehe etwas, glaube aber nicht, dass ich etwas sehe“, ist selbstwidersprüchlich.
Wenn mit „sehen“ „einsehen“ gemeint ist und mit „glauben“ „als wahr annehmen“, dann entsteht die Tautologie „Wir glauben, was wir glauben.“
Wenn mit „sehen“ die Funktion des Sehsinns gemeint ist und mit „glauben“ „als real annehmen“, dann ist der Satz „Wir sehen nur, was wir glauben.“ nicht notwendig wahr, denn ich kann den Pumuckl sehen, aber gleichzeitig nicht an seine reale Existenz glauben. Der Satz ist immer dann falsch, wenn wir etwas Überraschendes oder auch nur Neues sehen. Glaube ist keine notwendige Vorbedingung für eine Sinneswahrnehmung.
Der Zusammenhang zwischen Sehen und Glauben scheint nicht so einfach zu sein, er ist vielmehr erläuterungsbedürftig.
Die Bedeutung des Gesagten ist nun einmal kontextabhängig. Das macht Sprache schön und interessant. „Analogien sind Treibstoff und Feuer des Denkens“ (Douglas Hofstadter, Emmanuel Sander, 2013).
Alles was du schreibst ist irgendwie wahr, aber es geht an der Sache vorbei. Ich schreibe von erwartungsgetriebener Wahrnehmung. Was wir erwarten ist hier all das, was in unserem Gehirnkästchen irgendwie schon vorbereitet ist, was wir also sowieso schon „glauben“, um überhaupt wahrnehmen zu können.