Fraktale allerorten: Wissenschaft mit Schmackes

Ein Lob dem  Marktschreier

Der schwarze Schwan von Nassim Nicholas Taleb beschäftigt mich noch immer. Ich mag dieses Buch („The Black Swan“, 2007). Ich mag es, obwohl viel dummes Zeug drin steht und obwohl es vor Übertreibungen und Beschimpfungen strotzt. Vielleicht mag ich es gerade deshalb. Die Marktschreierei und der blühende Blödsinn sind so offensichtlich, dass sie schlimmstenfalls zu einem leicht erhöhten Blutdruck führen und sich aufmerksamkeitssteigernd, also dann doch durchaus positiv auswirken. Schon in meinem Blog-Artikel „Mensch ärgere dich“ sprach ich davon. Hier lege ich noch eins drauf.

Ich will auf Talebs Kernthema eingehen, nämlich auf die fraktalen Verteilungen, mit denen wir es seiner Meinung nach auf den meisten Gebieten unseres Lebens zu tun haben. Taleb entdeckt sie bei der Verteilung der Vermögen oder der Einkommen der Bürger eines Landes, bei den Verkaufszahlen von Büchern, bei Unfall- und Kriegsfolgen, im Zusammenhang mit terroristischen Attacken, in Börsennotierungen und bei vielen weiteren Erscheinungen.

Hinter all der Marktschreierei steckt einiges an nützlicher Mathematik. In Talebs populärwissenschaftlicher Darstellung mathematischer Zusammenhänge habe ich keine Fehler entdeckt. Die gesteigerte Aufmerksamkeit beim Lesen weitete meinen Blick und förderte das Nachdenken über Tragweite und Grenzen mathematischer Modellbildung.

Wiederbelebung eines aus der Mode gekommenen Themas

Im Grunde geht es in Talebs Buch um eine Klasse von Kurven, die seiner Meinung nach geeignet sind, alle der oben genannten Phänomene und noch viel mehr angemessen zu beschreiben.

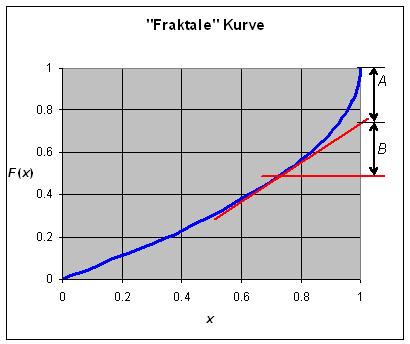Diese Kurven zeichnen sich durch eine Art Selbstähnlichkeit aus, sie sind in diesem Sinne fraktal. Die nebenstehende Grafik zeigt eine solche Kurve. Ihr Definitionsbereich liegt in Intervall von 0 bis 1 und ihr Wertebereich ebenso. Die Kurve wächst ausgehend vom Ursprung monoton bis zum Wert 1. Die Tangente an die Kurve und die waagrechte Linie durch den Berührungspunkt schneiden aus der rechten Begrenzungslinie die Abschnitte A und B aus (s. Grafik).  Die Kurve ist nun dadurch charakterisiert, dass das Verhältnis B/(A+B) für alle Punkte der Kurve dasselbe ist. Ich führe dafür die Konstante Epsilon ein: ε = B/(A+B).

Was ist an dieser Kurve fraktal? Wenn man die Grafik „herunterbricht“, indem man unten oder links von der Grafik etwas weglässt, dann bleibt die ε-Eigenschaft der Kurve erhalten. Insofern sind alle Teile der Kurve „selbstähnlich“. Allerdings ist das eine ziemlich triviale Art der Selbstähnlichkeit; denn sie ist einfach eine Folge der Tatsache, dass für die formbestimmende ε-Eigenschaft nur die rechte obere Ecke eine Rolle spielt, und dass uns diese Ecke beim „Herunterbrechen“ als Orientierungspunkt erhalten bleibt.

Mit der etwas weit hergeholten Terminologie gelingt Taleb der Anschluss an die „Chaostheorie“. Und diese Theorie löst bei Taleb ein wahres Feuerwerk der Begeisterung aus: Der Schöpfer der „Apfelmännchen“, Benoît Mandelbrod („The Fractal Geometry of Nature“, 1982), ist für ihn „einer der einflussreichsten Mathematiker in der Geschichte“, wohingegen Leute, deren Augen sich dieser Welt nicht geöffnet haben, für ihn Scharlatane sind, die nichts besseres zu tun wüssten, als ihre Studenten einer Gehirnwäsche mittels gaußscher Glockenkurve und ähnlicher Betrügereien zu unterziehen.

Das Gebiet des Chaos und der Fraktale ist an Marktschreiern nicht gerade arm. Dennoch ist es seit seiner Blütezeit in den Achtzigerjahren des letzten Jahrhunderts etwas aus der Mode gekommen. Es hat den verkündeten Anspruch nicht einlösen können, Erklärungen für alles Mögliche zu liefern. Übrig geblieben ist eine hübsche Spielerei, die jedenfalls schön anzusehen ist, die aber lediglich oberflächliche Computersimulationen für komplexe Erscheinungsformen des belebten und unbelebten Universums bieten kann.

Anwendung Lorenzkurve

Sehen wir vom marktschreierischen Chaos-Marketing einmal ab, so bleibt uns doch eine klar umrissene Klasse von Funktionen. Und wir erhalten von Taleb Hinweise darauf, inwieweit diese Kurven sich zur Beschreibung und Modellierung von Phänomenen eignen könnten, die mit dem üblichen Standardinstrumentarium kaum zu erfassen sind. Die Wertschätzung, die Taleb den „fraktalen“ Verteilungen entgegenbringt, hat nämlich einen tieferen Grund: Diese Verteilungen lassen Ausreißer zu —  „schwarze Schwäne“ in Talebs Sinn. Beispielsweise verfügte im Jahr 2009 die Hälfte der deutschen Haushalte über ein monatliches Nettoeinkommen von höchstens 1311 Euro (Wochenbericht des DIW Berlin Nr. 24/2010). Daneben gibt es Leute mit einem monatlichen  Einkommen von mehreren Millionen Euro. Die Superreichen sind zwar äußerst selten, aber eben keineswegs ausgeschlossen. Mit einer unterstellten Normalverteilung der Einkommen ist das jedenfalls nicht vereinbar, mit der fraktalen Verteilung schon.

Neu ist das alles nicht. Die Lektüre von Talebs Buch hat mich an einen Aufsatz von F. J. Radermacher zum Thema „Globalisierung“ (Informatik-Spektrum 6/2002) erinnert, in dem er die Klasse fraktaler Funktionen für die Charakterisierung der Ungleichverteilung von Einkommen in den Staaten dieser Erde verwendet. Sein Ausgangspunkt ist die Armutsdefinition der Europäischen Union. Nach dieser Definition gelten Menschen als arm, wenn sie über weniger als das halbe Durchschnittseinkommen verfügen.

Nun setzt Radermacher eine fraktale Einkommensverteilung voraus: Es mögen in einem bestimmten Land der Ärmste nur über einen Bruchteil ε des Durchschnittseinkommens verfügen. Lässt man nun alle Menschen weg, die über weniger als ein bestimmtes Einkommen verfügen, dann gilt für die übrigbleibende Population der Reicheren dasselbe: Der Ärmste unter ihnen verfügt über einen Bruchteil ε des Durchschnittseinkommens dieses reicheren Teils der Bevölkerung.

Für die Beschreibung der Einkommensverteilung einer Volkswirtschaft eignet sich die Lorenzkurve: Für jede nichtnegative Zahl x kleiner als eins teilen wir die Bevölkerung Ärmere und Reichere auf derart, dass die Ärmeren insgesamt einen Bruchteil x der Gesamtbevölkerung ausmachen. Der Anteil dieser Bevölkerungsschicht am Gesamteinkommen wird mit F(x) bezeichnet. In der grafischen Darstellung ergibt sich daraus die Lorenzkurve. Eine fraktale Einkommensverteilung führt zu einer fraktalen Lorenzkurve der oben gezeigte Art. Die Konstante ε nennt Radermacher Equity-Faktor.

Der Zusammenhang zwischen der fraktalen Einkommensverteilung und der fraktalen Lorenzkurve wird klar, wenn man bedenkt, dass die Steigung der Lorenzkurve proportional zum Einkommen der durch den x-Wert repräsentierten Bevölkerungsschicht ist und dass der Proportionalitätsfaktor der Anteil dieses Einkommens bezogen auf das mittlere Einkommen derjenigen ist, deren Einkommen wenigstens genauso groß ist.

Aber eins ist gewiss: Die Anpassung einer fraktalen Kurve an eine Einkommensstatistik ist kein zwingender Prozess mit eindeutigem Ergebnis: Je nach Anpassungsverfahren ergeben sich für dieselben Daten im Allgemeinen verschiedene Equity-Faktoren und damit auch verschiedene Lorenzkurven. Ob es gerechtfertigt ist, überhaupt eine fraktale Kurve anzusetzen oder ob man besser einen anderen Ansatz wählt, muss Gegenstand einer genauen Prüfung sein. Jedenfalls ist es nicht gerechtfertigt, die Selbstähnlichkeit als naturgegeben hinzunehmen. Chaos-Klamauk hilft da nicht weiter. Die fraktalen Kurven bilden nur einen von vielen möglichen Beschreibungsansätzen.

In der Studie „Lorenzkurven, Equity-Faktoren und schwarze Schwäne“ habe ich die mathematischen Hintergründe des „Schwarzen Schwans“ und des Equity-Ansatzes etwas ausführlicher dargestellt.

Emotionen in der Wissenschaft

Emotionen haben in der Welt der Wissenschaft einen schlechten Ruf. Aber sie können dem wissenschaftlichen Diskurs auch gut tun. Mit Verve vorgetragene Überzeugungen haben große Chancen, Gehör zu finden. Und manche wissenschaftliche Aussage bleibt im kollektiven Gedächtnis haften, weil im Streit auch einmal Unhaltbares, Skurriles, Kurioses oder Polemik im Spiel war. Ein paar Beispiele:

1. Der Streit um die Bedeutung der Fraktale findet in Talebs Buch „The Black Swan“ einen späten Nachhall. Die Sache hatte sich eigentlich schon anfangs der Neunzigerjahre erledigt, unter anderem mit dem Aufsatz „Chaos, Fraktale und das Bild der Mathematik in der Öffentlichkeit“ von Klaus Steffen (DMV Mitteilungen 1/1994, S. 25-40).
2. In der Ausstellung „WeltWissen – 300 Jahre Wissenschaften in Berlin“, die 2010 im Martin-Gropius-Bau in Berlin im Jahr 2010 stattfand, gab es im Raum zum Thema „Streit“ eine Tafel mit diesem Text: „»Der ist wohl die Puderquaste in den Nachttopf gefallen.« So die einzig überlieferte Reaktion im Publikum auf einen Vortrag der Medizinerin Rahel Hirsch 1907 vor der Gesellschaft der Ärzte der Charité. In ihren Ausführungen hatte sie – entgegen der herrschenden Lehrmeinung – nachgewiesen, dass größere, feste Partikel durch die Schleimhaut des Dünndarms gelangen und als Fremdkörper über den Harnweg ausgeschieden werden können.“
3. In der Unterhaltungsmathematik gab es vor vielen Jahren ein Leserbriefscharmützel zum Drei-Türen-Problem. Nachdem Marilyn vos Savant in ihrer Kolumne die korrekte Lösung vorgestellt hatte, wurde sie mit Spott überschüttet: „Unsere Fakultät hat herzlich über Sie gelacht“, „Vielleicht haben Frauen eine andere Sicht auf mathematische Probleme als Männer“, „Sie haben Unsinn verzapft“, „Darf ich den Vorschlag machen, dass Sie zunächst einmal in ein Standard-Lehrbuch über Wahrscheinlichkeitsrechnung schauen, bevor Sie das nächste Mal versuchen, ein derartiges Problem zu lösen?“, „Wieviele entrüstete Mathematiker braucht es, bis Sie endlich Ihre Meinung ändern?“ Marilyn vos Savant konterte trocken: „Lösungen mathematischer Probleme werden nicht durch Abstimmung entschieden.“ (Spektrum der Wissenschaft 11/1991, S. 12-16)

Der Drei-Türen-Streit mit seinen Entgleisungen hat für die mathematische Breitenbildung vermutlich mehr gebracht als alle didaktisch einwandfreien Bemühungen auf diesem Gebiet.