Risiko ist nicht objektivierbar

Sichtweisen auf das Risiko

Im Artikel Faktenjongleure und Statistikzauberer habe ich die von Hans Rosling propagierte optimistische Weltsicht aufs Korn genommen, insbesondere sein plattes Risikokalkül. Rosling unterscheidet das wahrgenommene vom realen Risiko und empfiehlt ausschließlich letzteres zum Maßstab von Entscheidungen zu machen. Es ist das sogenannte objektive Risiko, und das ist definiert als Schadenserwartungswert im rein mathematischen Sinn. Im einfachsten Fall ist dieses objektive Risiko gegeben durch die Formel Risiko = Schadenshöhe × Eintrittswahrscheinlichkeit.

Unter Maßgabe des objektiven Risikos ließe sich alles, was uns irgendwie ängstigt, richtig einordnen und wir brauchten uns nicht mehr allzu sehr vor Terrorismus, Pflanzengiften, Radioaktivität usw. zu fürchten (Rosling, 2018, S. 101-123). Die „faktenbasierte Weltsicht“ ist demnach alles, was wir benötigen, um die Welt, so wie sie ist, gut zu finden.

Diese Sicht der Dinge hat den Vorteil, dass sie das Individuum mit seinen subjektiven Gefahreneinschätzungen und seinen Launen aus den Überlegungen heraushält. Der Begriff des objektiven Risikos ist ein ideales Vehikel einer für jedermann verbindlichen Weltsicht. Der Neue Skeptiker – im Artikel Hochstapelei im Namen der Wissenschaft war von ihm die Rede – präferiert das objektive Risiko, denn so lassen sich nach seiner Auffassung Handlungsanweisung rein wissenschaftlich gewinnen. Es entsteht eine Wissenschaft der Moral (Shermer, 2015).

Florian Aigner schreibt am 28.4.2019 in seiner Futurezone-Kolumne zum Thema „Wissenschaftlich korrekte Panik“ ganz im Sinne des Neuen Skeptizismus: „Es wird immer schwierig sein, die Grenze zwischen gerade noch harmlosen und gerade schon gefährlichen Dingen zu ziehen. Aber wir sollten die Gefahren um uns wenigstens in die richtige Reihenfolge bringen und unsere Energie den größeren Gefahren widmen, anstatt uns vor Kleinigkeiten zu fürchten.“

Wenn von „richtiger Reihenfolge“ die Rede ist, dann lese ich das so: Es gibt eine richtige und von allen rational entscheidenden Menschen zu akzeptierende Reihenfolge der Gefahren.

Diese Prämisse ist unhaltbar, ebenso die Lehre vom objektiven Risiko als verbindliche Maßgabe der Gefahrenbewertung. Gerade der Skeptiker sollte wissen, dass menschliches Verhalten durch einfache mathematische Beschreibungen nicht zu erfassen ist. Das System Mensch und seine gesellschaftliche Einbindung sind dafür viel zu komplex.

Für Entscheidungen bei Risiko, denen sich der Einzelne gegenüber sieht, ist das reale oder objektive Risiko ein nur unzureichender Maßstab. Diese Unzulänglichkeit herauszustellen, dafür genügt mir im Folgenden ein ziemlich einfaches mathematisches Modell.

Die Neuen Skeptiker schießen über das Ziel hinaus. Aber in einem Punkt liegen sie wohl richtig: Unsere Ängste sind oft weit übertrieben und manch wirklich Bedrohliches nehmen wir nonchalant hin. Da ist ein Blick auf die Statistik ratsam, auf die Fakten. Dieser Blick verhilft uns dann zwar nicht zu einer allgemeinverbindlichen und von jedermann zu akzeptierenden Weltsicht, aber er hilft uns, unseren persönlichen „Angstmaßstab“ zu justieren.

Aber was sind die Fakten? Auch wer den „klassischen Gatekeepern“ (Pörksen) misstraut und den Internetforen allemal, kann sich einen Eindruck verschaffen. Er geht zu den Datenquellen und wendet ein wenig Dreisatzrechnung an.

Beispiel: Impfgegner kontra Impfpflicht

Im Falle des Hin und Her zur Masernschutzimpfung kann jedermann die Daten des Robert Koch Instituts (RKI) heranziehen. (Sollte er auch dieser Quelle misstrauen, ist er ziemlich verloren und es bleibt ihm letztlich nur Kaffeesatzleserei.)

Die Impfquote bei Schuleingangsuntersuchen liegt seit Jahrzehnten bei 90% (Epidemiologisches Bulletin, 4. Januar 2018 / Nr. 1). Von den 80 Mio. Einwohnern Deutschlands sind demnach etwa 72 Mio. gegen Masern geimpft. Die Impfung findet nur einmal in einem im Mittel 80 Jahre langen Leben statt. So kommt man – grob gerechnet – auf etwa 900 Tausend Masernschutzimpfungen je Jahr; es können aber auch gerade einmal 700 Tausend sein.

Die Zahl der anerkannten Impfschäden sinkt kontinuierlich (Meyer u. a., 2002). Im Jahr 1999 waren es 21. Über einen größeren Beobachtungszeitraum (1972-1999) gemittelt, gehen 1,1% der anerkannten Impfschäden auf die Impfungen gegen Masern und die Kombinationsimpfungen gegen Mumps, Masern und Röteln  zurück.  Sogar derartig grobe Abschätzungen lassen darauf schließen, dass einer Million Masernimpfungen schlimmstenfalls ein anerkannter Impfschaden zuzurechnen ist.

Andererseits weiß man um die Gefahren, die dem nicht Geimpften drohen: „Nach Angaben der WHO liegt in entwickelten Ländern die Letalität der Masern zwischen 0,05% und 0,1%.“ (https://www.rki.de/DE/Content/InfAZ/M/Masern/Masern.html)

Soweit sind das Daten. Inwieweit sie Fakten abbilden, kann dem einen oder anderen zweifelhaft erscheinen. Wer sie  anerkennt, muss diese Fakten noch irgendwie in seine Weltsicht einpassen. Und da fangen die eigentlichen Schwierigkeiten an. Unter anderen gibt es

• grundsätzlich Misstrauische, die überall Verschwörungen vermuten,
• Anhänger der Naturmedizin, die Impfung als unnatürlich verurteilen und ablehnen,
• gewisse Gottgläubige, die es ablehnen, mit Massenimpfungen Gott ins Handwerk zu pfuschen,
• diejenigen, die sich auf anekdotische Evidenz verlassen (,„Meine Tochter ist nicht geimpft worden und jedes Mal, wenn wir alle krank werden, ist sie die einzige, die nichts hat“),
• Leute, die den einfachen Regeln des Volkswissens vertrauen („Das Immunsystem funktioniert nur durch Kennenlernen“).

Die Zitate sind aus den Kommentaren zum ZEIT-Artikel von Schade u. a. (2015).

Der Skeptiker tritt gegen diese irrationalen Weltsichten an. Das ist aber nur ein Teil seiner faktenbasierten Mission. Selbst wenn er alle irrationalen Elemente eliminieren könnte, wäre er noch lange nicht beim objektiven Risiko als Grundlage aller rationalen Entscheidungen angekommen. Bereits unser Beispiel von der Impfgegnerschaft zeigt ein paar Hindernisse, die dem entgegenstehen.

Aufgrund der Impfrate von 90% sind die Masern in Deutschland sehr selten. Die Nichtgeimpften sind durch die Geimpften weitgehend geschützt. Das verringert die Wahrscheinlichkeit für Erkrankung der Ungeimpften. Impfverweigerung kann also durchaus eine rationale persönliche Entscheidung sein.

Die Erhöhung der Impfrate lässt sich über das erwartbare zukünftige Gemeinwohl rechtfertigen: Ausrottung der Masern. Mit dem Vorwurf der Trittbrettfahrerei wäre ich dennoch vorsichtig. Jedenfalls betreten wir hier das Feld der Moral und der Wertvorstellungen, und da reicht die objektive Risikobewertung nicht hin.

Subjektive Wertmaßstäbe sind rational

Ohne sichere Datenbasis sind Risikoerwägungen ziemlich sinnlos. Aber sie allein reicht nicht für ein Urteil. Die Situation des Entscheiders, sein Denkrahmen spielt eine große Rolle. Risiko ist unabweisbar subjektiv. Das lässt sich mit einer einfachen Modellvorstellung leicht einsehen.

Die meisten Menschen haben irgendwelche Wünsche. Manches steht ganz oben auf der Wunschliste, anderes eher unten. Es hängt von den persönlichen Lebensumständen und vom Wertesystem jedes Einzelnen ab, welches Hochgefühl die Erfüllung eines Wunsches bewirkt. Ich entwickle die Gedanken dazu an der fiktiven Gestalt „Horst“.

Horst hat eine Rangordnung seiner Wünsche erstellt. Ganz oben steht der Erwerb einer Eigentumswohnung. Bei einem „warmen Regen“ von 100 000 € wäre dieser Wunsch erfüllbar. Horst misst den hunderttausend Euro einen subjektiven Nutzen von 100 % zu: hundertprozentiges Hochgefühl bei einem Lottogewinn von hunderttausend Euro.

Aber auch die Hälfte davon wäre nicht übel. Nach Rücksprache mit der Familie stellt er fest: Die Eigentumswohnung wäre auch bei einem Gewinn von 50 000 € noch erschwinglich. Durch den Schuldendienst müssten andere, weniger dringliche Wünsche zurückgestellt werden. Er kommt zur Überzeugung, dass das Hochgefühl nicht etwa mit nur 50 %, sondern mit etwa 80 % zu veranschlagen wäre. Mit einem Gewinn von 25000 € läge –  verglichen mit dem vollen Gewinn von 100000 € – sein Hochgefühl immer noch deutlich über 50 %.

Horst ist Mathematiker; nach einigem Hin- und Her findet er eine Funktion, die sein Hochgefühl in Abhängigkeit vom Betrag wiedergibt, seine subjektive Nutzenfunktion.

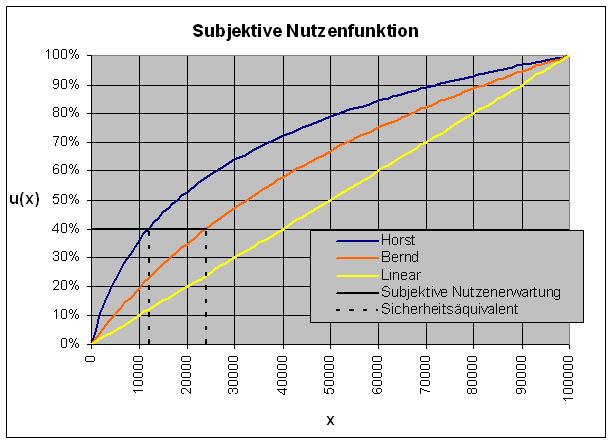
Horst sagt sich: Mein Hochgefühl hängt womöglich logarithmisch vom gewonnenen Betrag x ab. Bereits im 18. Jahrhundert hat Daniel Bernoulli einen solchen Ansatz gemacht. Die Nutzenfunktion u(x) stellt den subjektiven Nutzen in Abhängigkeit vom Betrags x dar. Zumindest für größere fünfstellige Beträge passt der Logarithmus. Bei kleinen Beträgen bin ich mir nicht so sicher: Zwei Euro sind mir doch tatsächlich doppelt so viel wert wie ein Euro. Also korrigiere ich die Formel, so dass für höhere Beträge näherungsweise das logarithmische und für kleinere näherungsweise das lineare Nutzengesetz gilt. Mit dem Ansatz u(x) = c∙ln(1+x/x₀) kann ich meine Empfindungen recht genau wiedergeben. Es handelt sich um eine Funktion mit von links nach rechts abnehmender Steigung. Der Ankerwert x₀ muss in der Übergangszone zwischen den Gültigkeitsbereichen des linearen und des logarithmischen Nutzengesetzes liegen. Ein plausibler Wert angesichts meiner Präferenzen ist 5000 €.“

Die sich so ergebende Kurve für Horst ist in der Grafik wiedergegeben. Die Nutzenfunktion ist linear, solange sich die Beträge im Rahmen des normalen Budgets halten.

Nehmen wir an, Horst bekommt die Gelegenheit, an der Börse oder sonst wo, auf einen Gewinn von 100 000 € zu wetten, bei einer Gewinnchance von 40%. Wieviel wäre ihm eine solche Wette wert?

Seine Nutzenkurve zeigt 40%-prozentigen Nutzen bei 12 000 €. Das ist das Sicherheitsäquivalent der Wette. Höchstens diesen Betrag wird Horst für die Teilnahme an der Wette bereitwillig einsetzen. Horsts Nachbar Bernd ist wohlhabender; sein Ankerwert liegt bei 30 000 €. Dementsprechend höher ist sein Sicherheitsäquivalent: 24 000 €. Je größer der Ankerwert, desto mehr nähert sich die Nutzenfunktion der linearen Nutzenfunktion an. Zur Rangfolge der Alternativen: Horst würde 20 000 € der Wette vorziehen. Für Bernd gilt die umgekehrte Rangfolge; er wettet lieber und setzt dafür die 20 000 € aufs Spiel.

Die Kurven oberhalb der linearen stehen für Risikoaversion: Der Spatz in der Hand ist mir lieber als die Taube auf dem Dach.

Für die subjektive Schadensfunktion übernehmen wir die Form der Nutzenfunktion. Ein deterministische Schaden, beispielsweise der Zeitverlust durch Verzicht aufs Überholen, wird gegenüber dem zufälligen Schaden eines möglichen Unfalls überbewertet. In der Schadensbetrachtung sind wir also risikofreudig.

Sowohl bei der Beurteilung von möglichen Schäden als auch beim Nutzenkalkül gibt es bei den hier gewählten Nutzen- und Schadensfunktionen eine Tendenz zur Überbewertung der Gewissheit. Diese Tendenz hat den Rang eines allgemeinen psychologischen Prinzips: Ein fester Nutzen wird gegenüber dem zufälligen präferiert, und ein zufälliger Schaden erscheint uns gegenüber festen Kosten eher erträglich – immer bei gleichem objektivem Risiko.

Es gibt Ausnahmen: Sogar die bei Gewinnaussichten eher risikoscheuen Leute spielen zuweilen Lotto. Und der risikofreudige Autofahrer hat eine Reihe von Versicherungen abgeschlossen, die objektiv gesehen jedenfalls ein Verlustgeschäft sind.

Der subjektive Nutzen und Schaden lässt sich also noch nicht einmal für eine Person in eine einfache Formel fassen. Es kommt auf den Denkrahmen an, innerhalb dessen eine Entscheidung fallen muss. Dieses Framing verstärkt den Zweifel an einer machbaren objektiven Risikobewertung weiter. Wer mehr darüber wissen will, sollte sich den Werken von Daniel Kahneman und Richard Thaler zuwenden.

Quellen

Kahneman, Daniel: Thinking Fast and Slow. 2011

Kahneman, Daniel; Tversky, Amos: Prospect Theory: An Analysis of Decision under Risk. Econometrica, Vol. 47, 2/1979, 263–291

Meyer/Rasch/Keller-Stanislawski/Schnitzler (RKI): Anerkannte Impfschäden in der Bundesrepublik Deutschland 1990–1999. Bundesgesundheitsbl – Gesundheitsforsch – Gesundheitsschutz, 2002 45:364–370

Pörksen, Bernhard: Die große Gereiztheit. 2018

Rosling, Hans: Factfulness. Ten reasons we’re wrong about the world – and why things are better than you think. 2018

Shermer, Michael: The Moral Arc. How science makes us better people. 2015

Thaler, Richard H.; Sunstein, Cass, R.: Nudge. 2008

Links

http://www2.hs-fulda.de/~grams/DecisionsUnderRisk/Risk.html

Von Blickle, Paul; Schadwinkel, Alina (24.2.2015): Masern sind viel gefährlicher als die Impfung.
https://www.zeit.de/wissen/gesundheit/2015-02/masern-impfung-risiko-nebenwirkung