Schöne Mathematik

Ein neuer Zweig der Mathematik entsteht

Kürzlich entdeckte ich ein populärwissenschaftliches Buch über die Anfänge der Wahrscheinlichkeitsrechnung. Es ist vom auch hierzulande beliebten britischen Autor Keith Devlin und trägt den Titel „Pascal, Fermat und die Berechnung des Glücks“ (englische Ausgabe 2008, deutsch 2009). Für Leute, die ihre mathematische Allgemeinbildung pflegen wollen, eignet es sich gut als Urlaubslektüre.

Im Zentrum des Buches steht ein Briefwechsel aus dem Jahre 1654 zwischen Blaise Pascal (ja, der mit dem „Pascalschen Dreieck“) und Pierre de Fermat (Entdecker des großen und des kleinen Fermatschen Satzes). Dieser Briefwechsel gab den Anstoß zur Entwicklung eines neuen Zweiges der Mathematik: der Wahrscheinlichkeitsrechnung. Die Wahrscheinlichkeitsrechnung ist also ein Kind der Neuzeit und sie hat sich zu einem sehr umfangreichen Zweig der Mathematik mit weitreichenden praktischen Anwendungen herausgebildet: Ohne die darauf aufbauende Risikoanalyse ist der moderne Verkehr mit Großflugzeugen, Hochgeschwindigkeitsbahnen und dichtem Straßenverkehr nicht vorstellbar, ebenso wenig das heutige Banken- und Versicherungswesen und auch nicht eine zeitgemäße Qualitätssicherung.

Gegenstand der brieflichen Auseinandersetzung zwischen Pascal (Paris) und Fermat (Toulouse) ist die Frage, wie der Einsatz unter den Beteiligten wohl aufzuteilen sei, wenn ein Spiel vorzeitig abgebrochen wird (Problem des abgebrochenen Spiels). Das umwerfende daran ist, dass hier wohl erstmals Mathematik betrieben wird, die sich nicht mit der Betrachtung des Vorhandenen und Gegenwärtigen begnügt, sondern die in die Zukunft hinausgreift: Es geht um Geschehnisse, die noch gar nicht eingetreten sind und die – da das Spiel ja nicht fortgesetzt werden soll – wohl auch nicht eintreten werden.

Machen wir das Problem konkret: Zwei Freunde, Albert und Bertrand, spielen gern und gleich gut Schach. Sie vereinbaren ein Spiel mit mehreren Partien und einem Einsatz von – sagen wir – fünfzig Euro für jeden. Gewonnen hat derjenige, der zuerst sechs der Schachpartien gewonnen hat. Die Runden ziehen sich in die Länge. Als Albert vier Runden und Bertrand drei Runden gewonnen hat, lenkt sie die gerade beginnende Fußballweltmeisterschaft vom Spiel ab. Sie fragen sich, wie sie bei Spielabbruch den Einsatz gerecht untereinander aufteilen sollen. Einfach halbe-halbe machen, das sieht auch Bertrand ein, ist ungerecht. Albert ist näher am Sieg als Bertrand: Er hätte nur noch zwei Spiele gewinnen müssen, und sein Freund immerhin noch drei. Aber wie lassen sich die Gewinnaussichten quantifizieren und in eine gerechte Aufteilung umsetzen?

Das ist im Wesentlichen die Frage, um die es Pascal und Fermat ging und für die beide ihre Lösungen austauschten. Ihre Lösungsansätze waren sehr verschieden, und sie führten zu denselben Ergebnissen: „La vérité soit la même à Toulouse qu’à Paris“. Und mit ihren Lösungsmethoden haben sie nichts Geringeres geschaffen als die moderne Wahrscheinlichkeitsrechnung. Getroffen haben sich die beiden nie.

Meinungsverschiedenheiten über Eleganz und Schönheit

Bevor ich die Lösungen skizziere, will ich sagen, worüber ich in dem Buch gestolpert bin. Devlin schreibt auf Seite 71, dass er auf eine detaillierte Beschreibung von Pascals Ansatz verzichte, „weil Fermats Lösung einfach weitaus eleganter ist“.

Oh ja, dem Mathematiker genügt es, wenn er einen allgemein gangbaren Lösungsweg vorfindet und wenn er für ein kleines und überschaubares Beispiel auch zu einem Ergebnis kommt. Auch eine schöne Summenformel mit Exponentialausdrücken und Binomialkoeffizienten findet er entzückend. Und in dieser Hinsicht ist Fermats Ansatz wohl mustergültig.

Leider geben die Briefe keine detaillierte Beschreibung der Lösungsverfahren: Pascals erster Brief ist verloren gegangen und auch Fermats Methode ist nirgends im Detail beschrieben. In beiden Fällen sind wir auf die Reflexionen Pascals angewiesen, die er hauptsächlich in seinem Brief vom 24. August 1654 anstellt.

Ich will zunächst beschreiben, welchen Lösungsweg Fermat wohl beschritten hat. (Es geht ums Grundsätzliche. Sollte Fermat es anders gemacht haben, dann nur unwesentlich.) Dabei bewege ich mich der besseren Verständlichkeit halber in unserem heutigen Begriffsgebäude. Man bedenke, dass sogar der Begriff „Wahrscheinlichkeit“ („probabilité“) in den damaligen Werken nicht in der heute gängigen Bedeutung vorkommt.

Nehmen wir einmal an, dass Albert noch zwei (a = 2) und Bertrand noch drei (b = 3) gewonnene Runden zum Sieg fehlen.

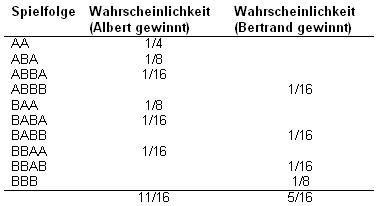
Eine Runde, die an Albert geht, bezeichnen wir mit A und eine für Bertrand mit B. Eine Folge bis zum Spielende könnte dann so aussehen: BABB. In dem Fall hat B das Spiel gewonnen. Nun listen wir alle möglichen Spielverläufe in lexikalischer Folge auf und schreiben dahinter die Wahrscheinlichkeit, mit der diese Folge vorkommt. (Voraussetzungsgemäß gewinnt jeder der Freunde eine Runde mit der Wahrscheinlichkeit 1/2).

Beispiel für Fermats Methode

Dieser Lösungsweg lässt sich verallgemeinern und es ergibt sich die oben bereits angekündigte schöne Formel für die Wahrscheinlichkeit eines Sieges für Albert. Diese Wahrscheinlichkeit sei mit e(a, b) bezeichnet. In unserem Beispiel haben wir den konkreten Wert e(2, 3)=11/16 errechnet. (Ich verzichte auf die Wiedergabe der allgemeinen Formel. Sie ist für das Folgende unwesentlich.)

Die Schönheit liegt im Auge des Betrachters, so heißt es. Und der Betrachter (Keith Devlin) ist in diesem Falle ein Mathematiker.

Mir jedenfalls, und ich sehe die Sache auch mit den Augen des Informatikers und Ingenieurs, hat Pascals Lösung, die Ausgangspunkt des Briefwechsels war, besser gefallen. Sie werden sehen, dass Pascals Methode die Werte e(a, b) mit geringerem Rechenaufwand liefert als Fermats Vorgehen, jedenfalls dann, wenn man sich für mehrere dieser Werte interessiert. (Dass für Pascal auch die praktische Anwendung der Mathematik hohen Rang hatte, sieht man an seiner bahnbrechenden Erfindung auf dem Gebiet der mechanischen Rechenmaschinen, an der Pascaline. Wer diese verstehen will, sollte bei Gelegenheit einmal mit dem Modell, das im Heinz Nixdorf MuseumsForum in Paderborn steht, experimentieren.)

Pascal bietet uns ein leicht zu verstehendes und praktisches Rechenverfahren an. Dessen Prinzip ist für die heutige Informatik grundlegend. Auch mit Pascals Ansatz lässt sich die oben erwähnte „schöne Formel“ gewinnen. Aber dazu sind mathematische Methoden notwendig, die Pascal noch nicht zur Verfügung standen.

Pascals allgemeine Methode

Mögen Albert noch a und Bertrand noch b gewonnene Runden bis zum Sieg fehlen. Das Ursprungsproblem lautet, die Wahrscheinlichkeit e(a, b) für einen Sieg Alberts zu bestimmen. Die Idee Pascals ist nun, die Werte a und b tatsächlich als variabel anzusehen. Er bettet das Problem sozusagen in eine allgemeinere Problemstellung ein und fragt nach einer Beziehung zwischen den zunächst noch unbekannten Werten e(a, b) für die verschiedenen a und b. Genau so war er ja bereits mit den Binomialkoeffizienten verfahren und ist auf das nach ihm benannte Dreieck gekommen.

Beim Spielstand (a, b) gewinnt Albert, wie stets, die nächste Runde mit der Wahrscheinlichkeit 1/2. Die Wahrscheinlichkeit, dass Albert die Runde und auch noch das gesamte Spiel gewinnt, ist demnach gleich e(a-1, b)/2, Die Wahrscheinlichkeit, dass Albert verliert und dennoch das gesamte Spiel gewinnt, ist gleich e(a, b-1)/2. Die Wahrscheinlichkeit, dass er beim Spielstand (a, b) das gesamte Spiel gewinnt, ist also gleich

e(a, b) = e(a-1, b)/2 + e(a, b-1)/2.

Damit haben wir die gesuchte Beziehung zwischen den Lösungsansätzen. Jetzt können wir die Lösungswerte berechnen, indem wir uns, ausgehend von den leicht zu ermittelnden Werten, Schritt für Schritt zu allen uns interessierenden Werten durchhangeln.

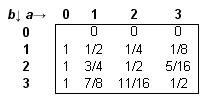
Offenbar gilt e(a, 0) = 0 für alle a: Bertrand hat bereits gesiegt. Außerdem ist e(0, b) = 1: Albert ist der Sieger. Über die Beziehung zwischen den Lösungsansätzen können wir nacheinander eine Tabelle für e(a, b) auffüllen:

Beispiel für Pascals Methode

Neben anderen haben wir wieder den Wert e(2, 3)=11/16 gefunden.

Pascals Ansatz erlaubt problemlos vielfältige Verallgemeinerungen. Also: Ich finde ihn wirklich schön.

Probieren Sie die Sache doch einmal aus: Nehmen wir einmal an, die zwei Freunde unterscheiden sich in der Spielstärke: Von je fünf Runden entscheidet im Mittel Albert drei für sich, während im Schnitt zwei an Bertrand gehen. Sie vereinbaren, dass derjenige von ihnen gewonnen hat, der sechs Runden für sich entschieden hat. In welchem Verhältnis sollten die Einsatzanteile der Freunde stehen, so dass beide eine Gewinnerwartung haben, die ihrem jeweiligen Einsatzanteil entspricht?

Antworten auf einige der noch offenen Fragen bietet das Excel-Arbeitsblatt AbgebrochenesSpiel.xls.

Anmerkung zu meinen Quellen: Neben Devlins Buch habe ich für diesen Artikel noch Aufzeichnungen von Paul-Louis Hennequin von der Universität Blaise Pascal in Clermont-Ferrand aus dem Jahre 2005 zu Rate gezogen: „Calculer des probabilités avec Blaise Pascal“. Die entscheidende Passage des Briefes Pascals an Fermat vom 29. Juli 1654 habe ich in der Schrift „Die Entwicklung des Wahrscheinlichkeitsbegriffs von 1654 bis 1718“ von Daniel Brönnimann, 24. September 2001, gefunden. Darin beschreibt Pascal seine Methode ganz einfach und klar. (Beide Schriften sind im Internet verfügbar.) Peter L. Bernstein schreibt in seinem Buch „Against the Gods“ (1996): „Fermat turned to pure algebra. Pascal was more innovative: he used a geometric format to illuminate the underlying algebraic structure“ (S. 63 f.).