Die Formel zur Berechnung der Impfeffektivität wurde im Hoppla!-Blog schon von oben und unten, von links und rechts betrachtet. Unbehaglich war mir nicht so sehr bei der Formel, sondern bei den in sie einfließenden Daten. Ich fragte mich,
- wie die Impfquote und die Hospitalisierungsdaten zusammenpassen,
- wie die nur teilweise Geimpften zu behandeln sind und
- wie die Genesenen darin unterzubringen sind.
Einige der Unschärfen des Datenmaterials werden vom Robert Koch-Institut angesprochen. Nun ergibt sich die Gelegenheit, noch einmal genauer hinzuschauen. Ein Kollege machte mich auf den Artikel Deep-Dive Impfeffektivität. Eine kritische Datenanalyse der RKI-Berechnungen/Teil 1: Die Methode von Simon Hegelich aufmerksam (Political Data Science, 19.12.2021).
Die im Artikel vorgebrachte Kritik am RKI-Monitoring ist ziemlich herb: „Entweder, die Daten sind verlässlich, oder die Erkenntnisse, die daraus abgeleitet werden, sind es auch nicht. Die hier beschriebenen Unwägbarkeiten sind eben nicht rein theoretisch, sondern wirken sich notwendig auf die Analyse aus. Wissenschaftlich wäre es, das eigene Unwissen zu akzeptieren und transparent zu kommunizieren, nicht aber, auf Basis falscher Daten Entscheidungen zu treffen.“
Ich will mir jetzt die wesentlichen Kritikpunkte vornehmen und eine Einschätzung abgeben, ob sie so schwerwiegend sind, wie behauptet.
Der Artikel beginnt mit einer kritischen Betrachtung der Formel für die Impfwirksamkeit. Hier ist sie noch einmal: 1-(1/q-1)/(1/d-1). Hierin ist q die Impfquote und d der Anteil der Geimpften an den Erkrankten (Durchbruchquote). Hegelich schreibt: „Sobald […] der Anteil der Geimpften an den Erkrankten sehr niedrig ist ODER die Impfquote sehr hoch ist, kann die Funktion nur Werte produzieren, die nahe 1 sind (also für eine sehr hohe Impfeffektivität sprechen).“ Diese Einschätzung kann ich nicht nachvollziehen. Die Werte der Formel hängen nie von einer der Quoten allein ab, sie werden nur dann deutlich größer als null, wenn die Durchbruchquote wesentlich geringer ist als die Impfquote.
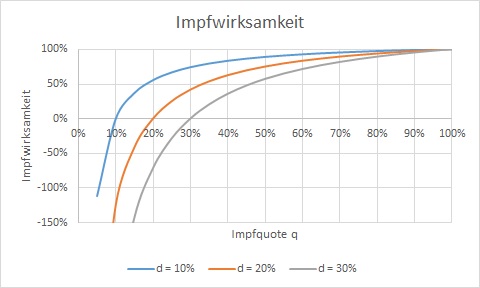
Für auffällig hält Hegelich, „dass die Effektivität (beim Endpunkt ‚Symptomatisch‘) bei den über 60-Jährigen in den letzten Wochen rapide gestiegen ist, von 63% auf 80%.“ Er meint, dass die Effektivität der Impfung nachlässt, gelte inzwischen als Common Sense und begründe derzeit vor allem die Notwendigkeit der Booster Impfungen. Wie aber sei es zu erklären, dass die Impfung plötzlich 17% an Effektivität gewinnt?
Ich habe mich auf die Hospitalisierten konzentriert. Dort ist dieser Effekt nur bei den Jungen aufgetreten. In diesem Fall ist die Datenbasis zu schwach für starke Aussagen. Genau das wird vom RKI auch angemerkt.
Das RKI rechnet in die Formel nur die vollständig Geimpften und die Ungeimpfte ein. Die einmal Geimpften werden nicht mitgerechnet. Hegelich merkt an: „Das Verhältnis der Geimpften zu Ungeimpft + Geimpft muss notwendig höher sein, als die Impfquote, die die Geimpften in der Altersgruppe zur Bevölkerung ins Verhältnis setzt.“ Aber genau das wird vom RKI berücksichtigt: „Für die Berechnung der Impfquoten wurden – wie bei den Impfdurchbrüchen – nur die vollständig Geimpften und Ungeimpften berücksichtigt.“
Hegelich kritisiert, dass bei der Errechnung der Impfquote der arithmetische Mittelwert verwendet wird, und nicht etwa das geometrische Mittel: „Bei den Zahlen 1 und 9 wäre das arithmetische Mittel 4.5, das geometrische 3. Sowohl der niedrige Wert 1 wie auch der hohe Wert 9 sind vom Mittelwert 3 um Faktor 3 entfernt. Wird aber das arithmetische Mittel genommen, dann wird die Impfquote systematisch überschätzt.“
Nehmen wir Zahlen, die der Situation eher angemessen sind: 70% und 80%. In dem Fall ist der arithmetische Mittelwert gleich 75% und der geometrische gleich 74,8. Die Wahl der Mittelwertbildung spielt also keine entscheidende Rolle.
Ein weiterer Kritikpunkt betrifft die Genesenen. Sie werden weder bei den Geimpften noch bei den Ungeimpften erfasst. Hegelich schreibt: „Wenn überproportional Genesene bei den Ungeimpften sind, dann wäre die Impfung wesentlich effektiver als sie erscheint. Man würde dann den Effekt der Impfung im Vergleich zu einer teilweise erlangten natürlichen Immunisierung messen, nicht aber die Wirksamkeit der Impfung. Umgekehrt: Wenn unter den Geimpften mehr Genesene sind, dann ist das, was wie der Effekt der Impfung aussieht in Wirklichkeit zum Teil ein Effekt der natürlichen Immunisierung.“
Auch dieser Effekt scheint mir eher marginal zu sein: Die Genesenen machen 6,5 Mio. von 83 Mio. aus. Das sind knapp 8%. Die beschriebene Unschärfe reduziert sich um eben diesen Faktor.
Der zweite Teil des Aufsatzes verspricht Aufhellung der Datenlage. Ich bin gespannt.

Spaß macht mir, Umständlichkeiten, eigene und die anderer, aufzudecken und zu bereinigen. Ich komme noch einmal auf die Formel für die Impfwirksamkeit zurück. Die Impfwirkskamkeit ist gleich 1-x/y = 1-(1/q-1)/(1/d-1).
Hegelich schreibt: „Sobald […] der Anteil der Geimpften an den Erkrankten sehr niedrig ist ODER die Impfquote sehr hoch ist, kann die Funktion nur Werte produzieren, die nahe 1 sind (also für eine sehr hohe Impfeffektivität sprechen).“
Wir gewinnen Klarheit über die Zusammenhänge, indem wir die Impfwirksamkeit bzw. das nach Impfung verbleibende relative Risiko als konstant betrachten: x/y = (1/q-1)/(1/d-1) = const. Als erstes fällt auf, dass bei konstanter Impfwirksamkeit entweder beide Größen (Impfquote q und Durchbruchquote d) gemeinsam gegen null gehen oder aber gemeinsam gegen eins. Interessant ist eigentlich nur der Proportionalitätsfaktor zwischen beiden Größen, der sich im Grenzfall einstellt.
Der Proportionalitätsfaktor ist leicht zu finden: Wir schreiben Zähler und Nenner der Formel für das relative Risiko jeweils als Bruch und machen aus dem sich ergebenden Doppelbruch einen einfachen Bruch: x/y = ((1-q)d)/((1-d)q). Für q und d gegen null ist x/y = d/q. Gehen q und d gegen eins, folgt x/y = (1-q) /(1-d). Die so definierten Geraden habe ich in die folgende Grafik für den Fall der 80-prozentigen Impfwirksamkeit (x/y = 20%) gestrichelt eingezeichnet.
Ich bin auch über diese Aussage von Hegelich gestolpert.
Die Funktion für die Impfwirksamkeit liefert in dem Fall 0/0 und mit L’Hospital sieht man, dass für q→1 die Wirksamkeit von der Ableitung der Funktion d = f(q) abhängt. Also genau der Funktion in ihrem Plot.
Die Impfwirksamkeit entspricht dem Kehrwert der Steigung dieser Funktionen für q → 1.
Je steiler der Anstieg, desto geringer ist x/y.
(ACHTUNG: VARIABLENBEZEICHNER MIT GEÄNDERTER BEDEUTUNG)
Zu der Aussage von Hegelich. Definiere:
Impfdurchbruchquotiernt PVC:=a
Impfquotiernt PPV:=b
Impfwirksamkeit w:
w = 1- (a/(1-a)) * (1-b)/b
Zitat Hegelich:
„Sobald […] der Anteil der Geimpften an den Erkrankten sehr niedrig ist ODER die Impfquote sehr hoch ist, kann die Funktion nur Werte produzieren, die nahe 1 sind (also für eine sehr hohe Impfeffektivität sprechen).“
Ich sehe dieses Problem nicht:
Wenn a und b exakte Werte haben (nicht fehlerbhehaftet sind), dann kann w exakt berechnet werden.
Allerdings habe ich mir Folgendes überlegt:
Wenn a bzw. b fehlerbehaftet („unscharf“) sind (d.h. innerhalb eines bestimmten Intervalls liegen), dann ist w ebenfalls fehlerbehaftet („unscharf“).
a ist z.B. unscharf, weil bei den Personen mit unbekanntem Impfstatus eine unbekannte Anzahl zu den geimpften Personen mit Impfdurchbruch gehören.
Genauso ist b unscharf (laut RKI).
Interessant ist das a-b-Gebiet mit hoher Steigung (egal in welcher Richtung), denn dort haben kleine Unschärfen von a bzw. b eine große Unschärfe von w zur Folge.
Ich betrachte nur mal die Steigung in a bzw. b Richtung:
dw/da = -(1-b)/b * (1/(1-a)^2))
dw/db = (a/(1-a)) * (1/b^2))
Dann gilt:
lim a–>1 dw/da = -unendlich
lim b–>0 dw/db = unendlich
Wenn also a in der Nähe von 1 liegt oder b in der Nähe von 0, dann wird w sehr unscharf.
(ACHTUNG: VARIABLENBEZEICHNER MIT GEÄNDERTER BEDEUTUNG)
Meine Ausführungen im meinem letzten Kommentar sind vielleicht nicht so interessant, da für eine hohe Impfwirksamkeit a in der Nähe von 0 und b in der Nähe von 1 liegen muss.
Darauf gehe ich im Folgenden ein:
Definiere:
Impfdurchbruchquotiernt PVC :=a
Impfquotiernt PPV :=b
Impfwirksamkeit w:
w = 1- (a/(1-a)) * (1-b)/b
x = P(E|U) = Quotient erkrankter Ungeimpfter
y = P(E|G) = Quotient erkrankter Geimpfter
Dann gilt:
w = 1 – y/x
also:
1-y/x = 1- (a/(1-a)) * (1-b)/b
y/x = (a/(1-a)) * (1-b)/b
r := x/y = (1-a)/a * b/(1-b)
Zitat Hegelich:
„Sobald […] der Anteil der Geimpften an den Erkrankten sehr niedrig ist ODER die Impfquote sehr hoch ist, kann die Funktion nur Werte produzieren, die nahe 1 sind (also für eine sehr hohe Impfeffektivität sprechen).“
Wenn man jetzt unter Impfeffektivität r das Verhältnis x/y versteht (also das Verhältnis als Ungeimpfter im Vergleich zu einem Geimpften zu erkranken), dann macht die Aussage von Hegelich für mich Sinn:
Wenn a bzw. b fehlerbehaftet („unscharf“) sind (d.h. innerhalb eines bestimmten unbekannten Intervalls liegen), dann ist r ebenfalls fehlerbehaftet („unscharf“).
a ist z.B. unscharf, weil bei den Personen mit unbekanntem Impfstatus eine unbekannte Anzahl zu den geimpften Personen mit Impfdurchbruch gehören.
Genauso ist b unscharf (laut RKI).
Interessant ist das a-b-Gebiet mit hoher Steigung (egal in welcher Richtung), denn dort haben kleine Unschärfen von a bzw. b eine große Unschärfe von r zur Folge.
Ich betrachte nur mal die Steigung in a bzw. b Richtung:
dr/da = -1/a^2 * (b/(1-b))
dr/db = 1/(1-b)^2 * (1-a)/a
Dann gilt:
lim a–>0 dr/da = -unendlich
lim b–>1 dr/db = unendlich
Wenn also a in der Nähe von 0 liegt oder b in der Nähe von 1, dann wird r sehr unscharf (kleine Ursache, große Wirkung).
Und genau das ist das Ziel der Impfmittelhersteller:
a —> 0 und b —> 1
mfg
Carl-Heinz Barner
Empfindlichkeitsanalyse
Die Impfwirksamkeit hängt von vielen Faktoren ab, beispielsweise vom Impfzeitpunkt und den geimpften Bevölkerungsgruppen.
Impf- und Durchbruchquote liefern in einem weiten Wertebereich ein stabiles Maß für die Impfwirksamkeit – immer bezogen auf die gerade herrschenden sonstigen Bedingungen.
Das spricht dafür, bei der Analyse der Formel, die Impfwirksamkeit als konstant anzunehmen.
Wenn wir aber die Empfindlichkeit der Impfwirksamkeit gegenüber den unvermeidlichen Schwankungen und Fehlern des Datenmaterials untersuchen wollen, sollten wir, wie Barner offenbar vorschlägt, die Impfwirksamkeit 1-x/y in Abhängikeit von der Impfquote q (Barners b) und der Durchbruchquote d (Barners a) separat betrachten.
Die angesprochenen Grenzübergänge a–>1 bei konstantem b und b–>0 bei konstantem a sind jedoch, abgesehen von den trivialen Grenzfällen a=b=1 und a=b=0, im Grunde undurchführbar: Es ist nicht anzunehmen, dass der Anteil der Geimpften im Krankenhaus größer ist als im Bevölkerungsdurchschnitt. Daraus folgt a<=b, in meiner Notation: d<=q.
Die Formel für die Impfwirksamkeit scheint doch ziemlich robust zu sein, anders als befürchtet. Auch der Folgeartikel von Simon Hegelich gibt Entwarnung:
https://politicaldatascience.blogspot.com/2021/12/impfeffektivitat-teil-2-rekonstruktion.html?m=1
Hier scheint sich ein Fehler eingeschlichen zu haben: x und y tauschen unbemerkt die Rollen. Untersucht wird von Barner der Kehrwert des relativen Risikos und nicht das relative Risiko.
>
>Hier scheint sich ein Fehler eingeschlichen zu haben:
>x und y tauschen unbemerkt die Rollen.
>Untersucht wird der Kehrwert des relativen Risikos und nicht das relative Risiko.
>
Das kann man doch auch untersuchen:
r = Verhältnis als Ungeimpfter im Vergleich zu einem Geimpften zu erkranken.
Und da zeigt sich, dass r empfindlich ist für:
a Nähe 0 und b Nähe 1
mfg
Barner
Freilich, Herr Barner, Sie betrachten den Kehrwert des relativen Risikos. Dieser ist genau dort empfindlich, wo das relative Risiko unempfindlich ist. Um das relative Risiko aber geht es, nicht etwa um dessen Kehrwert!
Das ist Ansichtssache:
Ein Ungeimpfter kann sich z.B. dafür interssieren, um ein Wievielfaches sein Erkrankungsrisiko größer ist als die eines Geimpften.
Beim Faktor r = 10 kann er sich schon so seine Gedanken machen…
mfg
Barner
Aus gutem Grund ist es üblich, die Zielgröße (den Impfeffekt) auf die Basisgröße zu beziehen und nicht umgekehrt. Genau das passiert beim relativen Risiko.
Im Artikel Schlank in 14 Tagen ist zu sehen, was man mit falsch gewählten Bezugsgrößen anrichten kann.
>
> Aus gutem Grund ist es üblich, die Zielgröße (den Impfeffekt) auf die Basisgröße zu
>beziehen und nicht umgekehrt. Genau das passiert beim relativen Risiko.
>
Was die Basisisgröße ist, ist m.M. nach Ansichtssache.
Beispiel:
Preis einer Ware nach Preiserhöhung.
D1) Verhältnis alter Preis / neuer Preis oder
D2) Verhältnis neuer Preis / alter Preis.
Was legt man als Basis fest?
Kommt auf den Standpunkt an, finde ich.
Egal wie man es macht:
Weder Definition D1 noch D2 sind kontraintuitiv, also möglich.
mfg
Barner
Ja möglich ist vieles. Aber es ist üblich, von einer Preiserhöhung um 10% zu sprechen; kaum einer sagt, dass es gestern 9% billiger war.
Der Unterschied zwischen Empfindlichkeitsbetrachtungen von Größen f und deren Kehrwert 1/f verflüchtigt sich, wenn man von der Empfindlichkeit (Ableitung f‘ bezüglich des Parameters) zur relativen Empfindlichkeit f’/f übergeht. Im Falle des Kehrwerts liefert die Formel dann
(1/f)’/(1/f) = (-f’/f^2)/(1/f) = -f’/f. Das ist, vom Vorzeichen abgesehen, derselbe Zahlenwert.
>
>Die Formel für die Impfwirksamkeit scheint doch ziemlich robust zu sein,
>anders als befürchtet.
>
Ja, das will ich im Folgenden begründen:
Behauptung:
„Kleine“ Änderungen der Durchbruchquote und der Impfquote haben „kleine Änderungen“ der Impfwirksamkeit w zur Folge, kurz gesagt:
w ist „gutmütig“ und unempfindlich.
Genauer:
Setze:
d := Durchbruchquote
q := Impfquote
w := Impfwirksamkeit
Es sei 0 <= delta_d <= 1 und 0 <= delta_q <= 1
Dann gilt für 2 beliebige Werte (d1,q1) und (d2,q2)
aus dem Intervall [0, delta_d] x [1- delta_q, 1]
w(d1,q1) – w(d2,q2) | <= delta_d/(1- delta_d) * delta_q / (1- delta_q)
Bemerkung:
Betrachte z.B. das Intervall [0; 0,3] x [0,7 ; 1]
Dann gilt für diese Differenz d:
d <= 0,3/0,7 * 0,3/0,7 ungefähr 0,184
Beweis:
Betrachte die Funktion:
w(d,q) = 1- d/(1-d) * (1-q) /q im Intervall [0, delta_d] x [1- delta_q, 1]
wobei gilt:
0 <= d < 1
0 < q <= 1
0 <= delta_d <= 1
0 <= delta_q <= 1
Wir suchen eine obere und eine untere Schranke für w:
1)
max w(d,q) = 1 (für z.B. d=0 und q =1)
2) Es gibt aber auch eine untere Schranke für w:
Da gilt:
a) 0 <= d <= delta_d
b) 1-delta_q <= q, also: <= 1-q <= delta_q
c) d = -delta_d, also 1–d >= 1-delta_d
d) q >= 1-delta_q
folgt daraus:
w(d,q) = 1- d/(1-d) * (1-q)/q >= 1 – delta_d/(1- delta_d) * delta_q / (1- delta_q)
Damit gilt für 2 beliebige Werte (d1,q1) und (d2,q2) aus dem
obigen Intervall [0, delta_d] x [1- delta_q, 1]
| w(d1,q1) – w(d2,q2)| <= 1- (1 – delta_d/(1- delta_d) * delta_q / (1- delta_q) )
<= delta_d/(1- delta_d) * delta_q / (1- delta_q)
mfg
Barner
Einverstanden. Aber es geht einfacher, denk ich:
Es ist
x/y = (1/q-1)/(1/d-1)
= 1/(1/(1-q)-1)*1/(1/d-1).
Sind sowohl d als auch 1-q nach oben durch Δ beschränkt, dann ist das relative Risiko x/y durch 1/(1/Δ-1)^2 nach oben beschränkt. Mit Δ = 0,3 ergibt das die Schranke 0,1836734694…
Wegen 0 <= x/y <= 0,1836734694 sind auch die Absolutwerte der Differenzen derartig begrenzter relativen Risiken durch die obere Schranke begrenzt. Diese Aussage überträgt sich auf die Impfwirksamkeit 1-x/y. Was das aber mit Robustheit zu tun hat, ist mir nicht klar. Ich werde noch einen Kommentar zu Empfindlichkeitsanalyse liefern.
>
>Aus gutem Grund ist es üblich, die Zielgröße (den Impfeffekt) auf die Basisgröße zu
>beziehen und nicht umgekehrt. Genau das passiert beim relativen Risiko.
>Im Artikel Schlank in 14 Tagen ist zu sehen, was man mit falsch gewählten
>Bezugsgrößen anrichten kann.
>
Im Institut für Statistik der LMU hat es Prof. Göran Kauermann genauso gemacht:
Um ein Wievielfaches ist das Erkrankungsrisiko eines Ungeimpften größer ist als die eines Geimpften.
Siehe Seite 2 unten und Seite 3 oben:
https://www.covid19.statistik.uni-muenchen.de/pdfs/codag-bericht-23.pdf
mfg
Barner
Die Empfindlichkeitsanalyse des relativen Risikos r = (1/q-1)/(1/d-1) bezüglich des Impfquotienten q führt auf ein besonders einfaches Ergebnis: Die relative Empfindlichkeit ist gleich
r’/r = -1/(q(1-q));
sie ist unabhängig von der Durchbruchquote d.
Die Empfindlichkeit des relativen Risikos für Fehler im Datenmaterial für q ist nur an den Rändern des Intervall [0, 1] sehr groß. Im praktisch interessanten Wertebereich führen moderate Datenfehler zu moderaten Fehlern in der Einschätzung der Impfwirksamkeit.
Dasselbe Ergebnis erhalten wir, abgesehen vom Vorzeichen, auch für die Durchbruchquote d. Die relative Empfindlichkeit bezüglich d ist gleich 1/(d(1-d)); sie ist unabhängig von p.
Nehmen wir die Daten des Hoppla!-Artikels Corona-Impfung: Risikoreduktion relativ und absolut.
Mit der Impfquote q=60% und einer Durchbruchquote von d=6% ist das relative Risiko für Hospitalisierung etwa gleich 4%. Die relative Empfindlichkeit bezüglich q ist gleich -4 und bezüglich d gleich 18 (gerundet). Eine um 1% geringere Impfquote (also 59% statt 60%) und eine um 1% höhere Durchbruchquote (7% statt 6%) führen also auf ein um etwa 22% höheres relatives Risiko, also auf etwa 5% statt auf 4%. Die Impfwirksamkeit ist dann etwa 95% statt 96%.
1)
Zitat:
„Die Empfindlichkeit des relativen Risikos gegenüber Fehlern im Datenmaterial für q ist nur an den Rändern des Intervall [0, 1] sehr groß.
Im praktisch interessanten Wertebereich führen moderate Datenfehler zu moderaten Fehlern in der Einschätzung der Impfwirksamkeit.“
Da bin ich anderer Meinung:
Zum interessanten Wertebereich gehören vor allem grosse Werte von q in der Nähe von 1 und kleine Werte von d in der Nähe von 0.
Denn das bedeutet eine hohe Impfwirksamkeit, die vor allem von Politikern und den Produzenten der Impfstoffe angestrebt wird, um die Impfstoffe besser vertreiben zu können.
2)
>
>Freilich, Herr Barner, Sie betrachten den Kehrwert des relativen Risikos.
>Dieser ist genau dort empfindlich,
>wo das relative Risiko unempfindlich ist. Um das relative Risiko
>aber geht es, nicht etwa um dessen Kehrwert!
>
…
>
>Aus gutem Grund ist es üblich, die Zielgröße (den Impfeffekt)
>auf die Basisgröße zu beziehen und nicht umgekehrt.
>Genau das passiert beim relativen Risiko.
>Im Artikel Schlank in 14 Tagen ist zu sehen, was man mit
>falsch gewählten Bezugsgrößen anrichten kann.
>
Für Prof Kauermann, einem Statistiker aus der LMU ist auch der Kehrwert des relativen Risikos wichtig (Seite 2 unten)
https://www.covid19.statistik.uni-muenchen.de/pdfs/codag-bericht-23.pdf
Für diesen Kehrwert ist aber für kleine d in der Nähe von 0 und große q in der Nähe von 1 die Empfindlichkeit bzw. relative Empfindlichkeit sehr groß:
Sowohl die Gesamtfehlergrenze als auch die relative Fehlergrenze nach den Definitionen in
https://de.wikipedia.org/wiki/Fehlerfortpflanzung
gehen gegen unendlich.
D.h. kleine Ursache (Unschärfe) große Wirkung.
mfg
Barner
Hallo allerseits,
1)
Meine Fragen (und Antworten) an Politiker, Experten, usw. zur Impfeffektivität und dem Corona-Komplex befinden sich unter:
https://umaterialien.de/corona/
2)
Prof. Hegelich von der LMU hat einen weiteren Artikel zur Corona-Diskussion verfasst:
https://politicaldatascience.blogspot.com/2021/12/impfeffktivitat-teil-3-die-impfung-hat.html
Leider kann ich die gerechneten, fiktiven Beispiele nicht ganz nachvollziehen.
Wie geht es euch ?
mfg
Barner
Die Berechnungen des Simon Hegelich sind nachvollziehbar, soweit ich das gesehen habe. Das Problem ist, dass er aus den möglichen Kombinationen von Altersgruppen, Impfstatus und Behandlung (Hospitalisierung ja/nein, intensiv ja/nein) diejenigen auswählt, die seine Argumentation stützen. Rosinenpickerei nennt man so etwas in Skeptikerkreisen.
Ein geschlossenes Bild bietet dahingegen die flächendeckende Darstellung der Wochenberichte des Robert-Koch-Instituts.
(Warum Hegelich Fiktives einflicht, versteh ich nicht. Der Wochenbericht ist doch konkret genug.)
1)
>
>Die Berechnungen des Simon Hegelich sind nachvollziehbar,
>soweit ich das gesehen habe.
>
Mir sind sie nicht nachvollziehbar:
M.M. nach gibt es Schreibfehler:
a) Schreibfehler:
Falsch:
PPV = 59112588 / (83155031 – 61608213) = 0.73
Richtig:
PPV = 59112588 / (59112588 + 83155031 – 61608213) = 0.73
b) Schreibfehler:
Falsch:
PPV = 31615849 / (83155031 – 61608213) = 0.59
Richtig:
PPV = 31615849 / (31615849 + 83155031 – 61608213) = 0.59
2)
Zitat:
———————-
Das RKI hat im Wochenbericht vom 30.12.2021 folgende Zahlen zu Omikron veröffentlicht:
Es wurden 6.788 Fälle von Omikron mit Angabe zu Symptomen übermittelt.
4.020 davon waren Vollständig geimpft,
1097 waren ungeimpft.
1.137 waren geboostert.
Über die verbliebenen 2.582 gibt es keine Information zum Impfstatus.
———————-
Im Wochenbericht vom 30.12.2021:
https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Situationsberichte/Wochenbericht/Wochenbericht_2021-12-30.pdf?__blob=publicationFile
habe ich in Tabelle 3 nur die folgende Zahl entdeckt:
Omikron Anzahl Gesamt = 5587
Woher stammen die anderen Zahlen von ihm?
3)
>
>Das Problem ist, dass er aus den möglichen Kombinationen von
>Altersgruppen, Impfstatus und Behandlung (Hospitalisierung
>ja/nein, intensiv ja/nein) diejenigen auswählt,
>die seine Argumentation stützen. Rosinenpickerei nennt man
>so etwas in Skeptikerkreisen.
>
a)Warum darf man so was nicht machen (d.h. konkret bestimmte Fälle untersuchen)?
b) Hegelich bezieht sich aber nur auf die Omikronvariante, die zu dem Zeitpunkt
Wochenbericht vom 30.12.2021 sehr schwach verbreitet war.
Deswegen ist das Ergebnis m.M. nach aussageschwach.
Würde er dieses Ergebnis heute liefern (wo die Omikronvariante dominierend wäre),
wäre es aussagestärker.
4)
Hegelich schreibt:
>
>Dafür müsste das RKI nur veröffentlichen,
>wie viele von den 124 Hospitalisierten geimpft waren.
>
Warum steht diese Info (Anzahl der Geimpften unter den Hospitalsierten) nicht im wöchentlichen Covid-19-Lagebericht vom 30.12.21:
https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Situationsberichte/Wochenbericht/Wochenbericht_2021-12-30.pdf?__blob=publicationFile
Im wöchentlichen Covid-19-Lagebericht vom 3.2.22 wird diese Info dagegen mitgeteilt:
https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Situationsberichte/Wochenbericht/Wochenbericht_2022-02-03.pdf?__blob=publicationFile
Warum ?
Die Berechnungen des Simon Hegelich sind für Sie nicht nachvollziehbar, auch wegen der Schreibfehler. Das sehe ich ein. Hegelichs Zahlenwerk im Detail nachzurechnen, fand ich nicht so prickelnd. Mir ging es darum festzustellen, dass seine Schlussfolgerungen nicht im Widerspruch zum aktuellen Zahlenwerk des Robert Koch-Instituts stehen.
Ich habe in Hegelichs Argumentation Rosinenpickerei gesehen, für Sie war es ein Aufzeigen von Schwachstellen. Der Sicht könnte ich mich anschließen, schriebe Hegelich nicht verallgemeinernd: „Wie ich im ersten Teil dargestellt habe, ist die Farrington-Formel bei hoher Impfquote eigentlich ungeeignet. Hinzu kommt, dass die gesamte Datenlage mehr als fragwürdig ist.“
Dem halte ich entgegen: Die Formel kann nichts dafür, die Gefahr droht vom Anwender (frei nach Robert Lembke). Besondere Aufmerksamkeit verdient tatsächlich die Datenbasis: Erfassungsmängel schlagen sich im Ergebnis nieder. Dass die Formel an den Gültigkeitsgrenzen (Impfquote gegen 100%) Ungenauigkeiten des Datenmaterials übermäßig verstärken könnte, wie Hegelich meint, dafür spricht nichts. Das habe ich im Kommentar zum Hoppla!-Artikel „Impfwirksamkeit: Statistiken richtig interpretieren“ versucht zu zeigen:
https://www2.hs-fulda.de/~grams/hoppla/wordpress/?p=2008#comment-7600
Viel interessanter als die Werte an den Gültigkeitsgrenzen der Formel sind die Fälle, in denen die Impfquote und die Durchbruchquote nahezu gleich groß sind. Dann kann es aufgrund von Schwankungen im Datenmaterial nicht nur zu sehr kleinen Werten der Impfwirksamkeit
kommen, sondern sogar zu negativen.
Gerade jetzt, wo die Omikron Variante des Coronavirus Oberhand gewinnt, beobachten wir eine abnehmende Impfwirksamkeit. Da aber gleichzeitig die Inzidenzen stark abnehmen, wird die Impfung auch nicht mehr so dringend gebraucht.
Ich entnehme ein passendes Zahlenbeispiel dem
wöchentlichen Lagebericht des RKI zur Coronavirus Krankheit (COVID 19) vom 10.02.2022:
Für die 12- bis 17- Jährigen haben wir derzeit eine Grundimmunisierung mit der Quote q = 53%. Die Durchbruchquote bei den hospitalisierten Coronafällen beträgt d = 30%. Daraus ergibt sich die ziemlich geringe Impfwirksamkeit von nur 62%. Da in dieser Gruppe im betrachteten Zeitraum nur insgesamt 50 Hospitalisierungen zu verzeichnen waren, haben wir (glücklicherweise) eine sehr schmale Datenbasis und damit einhergehend eine große Unschärfe des Ergebnisses.
>
>Dem halte ich entgegen: Die Formel kann nichts dafür,
>die Gefahr droht vom Anwender (frei nach Robert Lembke).
>Besondere Aufmerksamkeit verdient tatsächlich die Datenbasis:
>Erfassungsmängel schlagen sich im Ergebnis nieder.
>Dass die Formel an den Gültigkeitsgrenzen (Impfquote gegen 100%)
>Ungenauigkeiten des Datenmaterials übermäßig verstärken könnte,
>wie Hegelich meint, dafür spricht nichts.
>Das habe ich im Kommentar zum Hoppla!-Artikel „Impfwirksamkeit:
>Statistiken richtig interpretieren“ versucht zu zeigen:
>https://www2.hs-fulda.de/~grams/hoppla/wordpress/?p=2008#comment-7600
>
Für Hegelich kann das ja stimmen (habe es noch nicht nachgeprüft),
aber:
Die Ungenauigkeiten des Datenmaterials werden aber übermäßig verstärkt,
wenn man die Berechnung von Kauermann zu Grunde legt.
Hier mein Zitat vom 9.1.22 23:03 2)
——————————————————————
Für Prof Kauermann, einem Statistiker aus der LMU ist auch der
Kehrwert des relativen Risikos wichtig (Seite 2 unten)
https://www.covid19.statistik.uni-muenchen.de/pdfs/codag-bericht-23.pdf
Für diesen Kehrwert ist aber für kleine d in der Nähe von 0 und
große q in der Nähe von 1 die Empfindlichkeit bzw. relative
Empfindlichkeit sehr groß:
Sowohl die Gesamtfehlergrenze als auch die relative Fehlergrenze
nach den Definitionen in
https://de.wikipedia.org/wiki/Fehlerfortpflanzung
gehen gegen unendlich.
D.h. kleine Ursache (Unschärfe) große Wirkung.
——————————————————————
Kauermann berechnet:
x/y
also:
x/y= (1-d)/d * q/(1-q)
Da macht es dann schon einen Unterschied bei der Berechnung (Zitat Kauermann):
„Risiko eines Ungeimpften im Vergleich zum Risiko eines Geimpften“
wie genau q in der Nähe von 1 und d in der Nähe von 0 ist.
Sei f(x) = x die Wahrscheinlichkeit für eine Person, in einem bestimmten Zeitraum zu erkranken. Dann ist g(x) = 1/x die Anzahl der Personen mit genau einem Erkrankten. Sei f(x) = 1%, dann ist eine von hundert Personen krank, g(x) = 100.
Die relativen Empfindlichkeiten sind f'(x)/f(x) = -g'(x)/g(x) = 1/x = 100. Das sieht nach viel aus. Daraus folgt für die Empfindlichkeiten: f'(x) = 1 und g'(x) = -10000. Letztere ist nun geradezu riesig, absolut gesehen.
Da wir uns im Bereich von Prozenten aufhalten, sollten wir bei den Differenzen nur Werte im Promille-Bereich wählen, schon reduzieren sich die Variationen des Ergebnisses ganz erheblich.
Um einen Eindruck von den Grössenordnungen zu bekommen, verlassen wir den Bereich der kleinen Differenzen. Wir halbieren die Krankheitswahrscheinlichkeit, das ist absolut gesehen die Verringerung um ein halbes Prozent, also auf den Wert 1/200. Damit kommt ein Erkrankter auf 200 Personen, das ist zwar ein Mehr von 100 Personen, aber doch nur eine Verdopplung.
Die Einführung des Kehrwerts ändert selbstverständlich nichts an der Situation. Es handelt sich um bloße Augenwischerei.
>
> Die Einführung des Kehrwerts ändert selbstverständlich
> nichts an der Situation.
> Es handelt sich um bloße Augenwischerei.
>
Leider habe ich Ihre Rechnungen nicht nachvollziehen können.
Macht aber nichts, da es mir konkret um die Berechnung von Kauermann
und die Empfindlichkeit geht:
„Risiko eines Ungeimpften im Vergleich zum Risiko eines Geimpften“ =
(1-d)/d * q/(1-q)
Beispiel_1: d=0,27, q=0,97
(1-d)/d * q/(1-q) = (1-0,27)/0,27 * 0,97 / (1-0,97) = 87,49
Beispiel_2: d=0,26, q=0,98
(1-d)/d * q/(1-q) = (1-0,26)/0,26 * 0,98 / (1-0,98) = 139,46
Beispiel_3: d=0,25, q=0,99
(1-d)/d * q/(1-q) = (1-0,25)/0,25 * 0,99 / (1-0,99) = 297
Man sieht also, dass
„Risiko eines Ungeimpften im Vergleich zum Risiko eines Geimpften“
empfindlich gegenüber d und q ist, wenn q nahe 1 und d nahe 0 ist.
Wobei hier d noch nicht einmal nahe bei 0 ist.
Studenten haben mir schon vorgeworfen, dass ich oft zu viel Geduld aufbringe. lch fürchte, dass zuviel Geduld auch diesem Blog nicht gut tut.
Ich will bald zum Ende kommen mit der Frage, ob man bei der Berechnung der Impfwirksamkeit anstelle des relativen Risikos dessen Kehrwert nehmen sollte. Denn es ist einfach egal. Das sieht man an den relativen Empfindlichkeiten, die, abgesehen vom Vorzeichen, für beide Betrachtungsweisen völlig gleich sind.
Dass die relative Empfindlichkeit an den Rändern des Gültigkeitsintervalls betragsmäßig sehr groß wird, ist belanglos, denn an den Rändern, also für d gegen 0 und für p gegen 1, gibt es nicht mehr viel zu variieren; das heißt, dass die Variationsspielräume der Parameter d und p sehr klein werden. Daraus folgt, dass sich die Variationen der Impfwirksamkeit in Grenzen halten.
Über andere Fragen können wir gern einen neuen Diskussionsfaden beginnen.