Denksport am Rande des Wahnsinns II: Unendlich

Veröffentlicht am 5. Juni 2021 von Timm Grams

Im ersten Teil von „Denksport am Rande des Wahnsinns“ ging es um Mathematik in der Schule, speziell um die vollständige Induktion und um Optimierungsaufgaben. Im zweiten Teil suche ich nach Antworten auf die Frage, was es mit dem Grundstoff der Mathematik, mit den Zahlen, auf sich hat.

Die Welt der Zahlen

Die größte Zahl

Der Name der größten Zahl stammt von einem Kind. Sein Onkel, ein Mathematiker, hatte die Zahl an die Tafel geschrieben und das Kind meinte, dass das wie ein Googol aussehe. Unter Beteiligung von etwas Legasthenie wurde daraus später der Name der heute beliebtesten Suchmaschine  im Internet. Wen die ganze Geschichte interessiert, der möge diese Suchmaschine bemühen oder in „Eine kleine Geschichte der Unendlichkeit“ von Brian Clegg nachsehen (2015, S. 57).

Im Alltagsleben kommt man immer mit deutlich kleineren Zahlen aus. Dem Googol kommt mit Fug und Recht das Prädikat zu, die größte Zahl zu sein. Und wie groß ist nun ein solches Googol? Jedenfalls ist es größer als die Anzahl der Atome im Universum. Ein Googol ist eine Eins gefolgt von einhundert Nullen: 10.000.000.000.000.000.000.000.000.000.000.000.
000.000.000.000.000.000.000.000.000.000.000.
000.000.000.000.000.000.000.000.000.000.000

Linien bestehen aus Punkten, oder?

Jede Strecke besteht aus Punkten. Soweit herrscht Einvernehmen. Aber: Wie viele sind es? Jetzt ist es mit der Einigkeit vorbei. Nähern wir uns der Angelegenheit ganz vorsichtig, indem wir mit dem Vergleichen beginnen,

Wir sprechen beim Umfang oder bei der Größe von Mengen besser von Mächtigkeit, wenigstens sobald wir den Bereich der endlichen Mengen verlassen. Zwei Mengen haben dieselbe Mächtigkeit, wenn es eine Eins-zu-eins-Abbildung zwischen ihren Elementen gibt. Haben die Mengen nur endlich viele Elemente, dann ist die Mächtigkeit gleich der Anzahl dieser Elemente. Die Menge {A, B, C} hat die Mächtigkeit 3, genauso die Menge aus einem Apfel, einer Birne und einer Zitrone. Nimmt man zu einer solchen endlichen Menge ein weiteres Element hinzu, erhöht sich deren Mächtigkeit um eins.

Nehmen wir die Menge der natürlichen Zahlen, dann kann man ein weiteres Element hinzufügen und es entsteht eine Menge derselben Mächtigkeit: Nach wie vor lassen sich alle Elemente abzählen,  zum Beispiel so: 1 ist die Nummer des hinzugefügten Elements, 2 die Nummer für die 1, 3 die Nummer für die 2 usw. Es gibt also eine Eins-zu-eins-Abbildung zwischen der Menge der natürlichen Zahlen und der neu gebildeten Menge mit einem zusätzlichen Element.

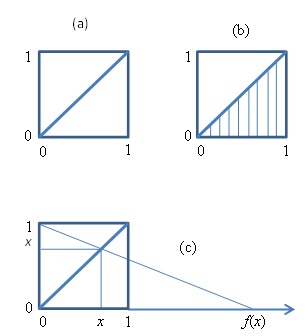Wir vergleichen zwei Strecken. Nehmen wir eine Seite des Einheitsquadrats und vergleichen diese mit der Diagonalen, Bild (a). Es gibt eine Eins-zu-eins-Abbildung von allen Punkten der einen Strecke zu denen der  anderen, wie in Bild (b) angedeutet. Die Punktmengen der Strecken haben folglich dieselbe Mächtigkeit, obwohl die Strecken offensichtlich ungleich lang sind (Lietzmann, 1962, S. 120). Der Wahnsinn schimmert auf.

Bild (c) zeigt, dass die Menge der Punkte von 0 bis 1 dieselbe Mächtigkeit hat, wie die Menge der Punkte von 0 bis unendlich. Eine Funktion, die jedem Zahlenwert des Intervalls von 0 bis 1 umkehrbar eindeutig einen Wert des positiven Zahlenstrahls zuordnet, ist f(x) = x/(1-x).

Die Punkte zeigen hier ihre unheimliche Seite. Sie sind unendlich klein, sie entziehen sich der Anschauung; wir nennen sie Infinitesimale. Es ist kein Wunder, dass man sie über Jahrhunderte hinweg möglichst ignorierte und schließlich sogar verbot, sich mit ihnen in der Lehre zu befassen. Weiterlesen →

Veröffentlicht unter Bildungswesen, Denksport, Logik, Naturwissenschaften, Physik, Problemlösen, Schule und Hochschule | Verschlagwortet mit , , , , | 11 Kommentare

Denksport am Rande des Wahnsinns I: die Ochsentour

Veröffentlicht am 28. Mai 2021 von Timm Grams

Bevor Sie meine Provokation mit wütenden Entgegnungen kommentieren, widerspreche ich mir vorauseilend gleich selbst. Die Denksportaufgaben habe ich in Büchern gefunden, die ich für wertvoll halte. Darin sind interessante Problemstellungen zu finden und die vorgeschlagenen Lösungsverfahren sind in technischen und wissenschaftlichen Zusammenhängen von großem Nutzen. Nur sind sie den zu lösenden Aufgaben nicht angemessen. Es wird sozusagen mit Kanonen auf Spatzen geschossen. Und darin liegt ein weiterer Wert dieser Bücher: Sie regen dazu an, nach besseren und einfacheren Lösungen zu suchen nach dem Motto: „Es geht immer noch einfacher.“ Das ist meine Basisheuristik. Mathematik sollte glücklich machen, eine Art Denksport sein. Diese Absicht verfolge ich auch in Klüger irren – Denkfallen vermeiden mit System (2020).

Den Wahnsinn sehe ich dann um die Ecke kommen, wenn die mathematische Beschäftigung zur Routine wird oder auch, wenn prima Konzepte mittels nervtötender Beispiele eingeführt werden. Darum geht es im ersten Teil von „Denksport am Rande des Wahnsinns“. Im zweiten Teil wende ich mich dann dem Unendlichen zu, das ja in der Mathematik sein Zuhause hat und in der Natur praktisch nicht vorkommt. Das hat schon etwas Unheimliches, einen Anflug von Wahnsinn.

Schulmathematik

Vor nunmehr fast zwei Jahrzehnten fiel mir auf, dass meine Kollegen Mathematikkurse für Studienanfänger anboten, in denen sie Schulstoff vermittelten. Sie boten den Schülern also das  an, was bei den Adressaten bereits in der Schule keinen nachhaltigen Eindruck hinterlassen hatte: Die meisten der  Studienanfänger waren auf ein technisches Studium nicht vorbereitet worden. Ihnen fehlte es an Fertigkeiten im Rechnen und am Verständnis für grundlegende mathematische Sachverhalte.

Das Problem wurde von den üblichen Brückenkursen nicht gelöst. Ich dachte über ein neues Konzept nach, das im Fuldaer Brückenkurs Mathematik (FBΣ) dann auch umgesetzt wurde. Im Zuge der Vorbereitung hatte ich ein ernüchterndes Erlebnis. Ich studierte die Lehrpläne einiger Bundesländer für ihre Gymnasien und fand nirgendwo das Thema vollständige Induktion, mit Ausnahme Bayerns. Aber auch dort rangierte es ganz hinten: „Die Vollständige Induktion [..] sollte nicht zu sehr vertieft werden“.

Dabei ist die vollständige Induktion etwas, das die Leistungsfähigkeit und Schönheit der Mathematik besonderes sinnfällig macht. Den Schülern wird Wichtiges vorenthalten. Stattdessen quält man sie unablässig mit Optimierungsaufgaben, die sich mittels Differentialrechnung nach festem Schema abhandeln lassen. Im nächsten Abschnitt bringe ich Beispiele dafür, wie diese Sekundarstufen-II-Routine Kreativität bremst.

Bleiben wir zunächst bei der vollständigen Induktion. Soweit ich dem Internet entnehmen kann, wird sie auch heute noch an Beispielen eingeführt, die nur zu zeigen scheinen, dass das Werkzeug eigentlich überflüssig ist. Ein gern genommenes Beispiel ist der Beweis dafür, dass die Summe der ersten n natürlichen Zahlen gleich n(n+1)/2 ist. Weiterlesen →

Veröffentlicht unter Bildungswesen, Denksport, Heuristik, Problemlösen | Verschlagwortet mit , | Ein Kommentar

Wie real ist unendlich?

Veröffentlicht am 16. März 2021 von Timm Grams

Nach dem Heute gibt’s ein Morgen, danach ein Übermorgen, und so weiter – endlos, solange nicht ein „Jüngstes Gericht“ dazwischenkommt. Wir zählen 1, 2, 3, … und haben nicht die geringste Schwierigkeit, uns das Unendlich vorzustellen. Zu Beginn meines Studiums hatte ich ein bestürzendes Erlebnis.

Die Russellsche Antinomie

Eine Studienfreundin behauptete, es war auf einer Party, dass die Mathematik gar nicht exakt und sogar in sich widersprüchlich sei. Die dort verwendeten Mengen seien gar nicht einwandfrei definiert, beispielsweise könne es die Menge aller Mengen nicht geben. Ich widersprach. Ein Freund aus einem höheren Semester sprang ihr bei. So lernte ich die Russellsche Antinomie kennen: Wir betrachten nur Mengen, die sich selbst nicht als Element enthalten. Das sind also Mengen, denen wir normalerweise begegnen. Die Menge der natürlichen Zahlen beispielsweise enthält alle natürlichen Zahlen, also 1, 2, 3, usw., nicht aber die Menge der natürlichen Zahlen. Markieren wir die Mengenbildung mit den geschweiften Klammer, dann schreiben wir die Menge der natürlichen Zahlen so: {1, 2, 3, …}. Wir können zwar die Menge {1, 2, 3, …, {1, 2, 3, …}} bilden, aber das ist nicht mehr dieselbe Menge wie die der natürlichen Zahlen; sie umfasst neben den natürlichen Zahlen auch die Menge der natürlichen Zahlen. Auch sie enthält sich nicht selbst.

Nun definieren wir eine Menge U derart, dass sie alle Mengen enthält, die sich selbst nicht als Element enthalten. Diese Gesamtheit der Mengen, ich nenne sie einmal unser Universum, ist selbst eine Menge. Wir fragen uns, ob U von derselben Art ist wie seine Elemente.

Wir fragen also, ob diese Menge U sich selbst enthält: Falls ja, dann enthält sie sich definitionsgemäß nicht; falls nein, dann doch. Der Selbstwiderspruch ist offenbar. Die Studienfreundin lag also ganz richtig mit ihrem Misstrauen gegenüber einem naiven Mengenbegriff.

Aus der Russellschen Antinomie habe ich eine Lehre für das Leben gezogen: Nimm dich in Acht vor Dingen, die allzu groß sind! Weiterlesen →

Veröffentlicht unter Bildungswesen, Denksport, Logik, Naturwissenschaften, Schule und Hochschule, Skeptizismus | Verschlagwortet mit , , | 4 Kommentare

Das fünfte Welträtsel: Bewusstsein

Veröffentlicht am 28. Dezember 2020 von Timm Grams

Mein humanistisch gebildeter Freund neckt mich, indem er hin und wieder lateinischeBrocken fallen lässt – da reicht meine Oberrealschulbildung nicht hin. Geist kontra Materie, ein alter philosophischer Streit schimmert da durch. Unterschiedliche Denkrahmen eröffnen unterschiedliche Sichtweisen. Dass unsere Ansichten dennoch verblüffend oft konvergieren, schafft eine gewisse Treffsicherheit im Urteil.

Ignorabimus?

Bei Gelegenheit höre oder lese ich von ihm das Zitat „Ignoramus et ignorabimus“. Ich schlage nach und erfahre, was das heißt: „Wir wissen es nicht und wir werden es niemals wissen.“ Dieser Ausspruch ist der Gipfelpunkt eines Vortrags eines gewissen Emil du Bois-Reymond von vor knapp eineinhalb Jahrhunderten. So erfahre ich von diesem, großen Physiologen und Philosophen, der die elektrische Natur der Nervensignale aufdeckte und sie dadurch der Messung zugänglich machte.

Du Bois-Reymond formulierte damals, was er acht Jahre später in einer Reihe von sieben Welträtseln als das fünfte benannte: Das Entstehen der einfachen Sinnesempfindungen. Er schreibt (du Bois-Reymond, 1882, S. 35 ff.): „Ich fühle Schmerz, fühle Lust, schmecke Süßes, rieche Rosenduft, höre Orgelton, sehe Rot […] Es ist eben durchaus und für immer unbegreiflich, dass es einer Anzahl von Kohlenstoff-, Wasserstoff- Stickstoff-, Sauerstoff- usw. Atomen nicht sollte gleichgültig sein, wie sie liegen und sich bewegen, wie sie lagen und sich bewegten, wie sie liegen und sich bewegen werden. Es ist in keiner Weise einzusehen, wie aus ihrem Zusammenwirken Bewusstsein entstehen könne.“

Du Bois-Reymond sieht hier Grenzen der Naturerkenntnis und er beschließt seinen Vortrag mit dem markanten „Ignorabimus!“

So unmittelbar und unverfälscht uns der rote Hut, das zustimmende Nicken, die Skyline von Frankfurt, die pochenden Töne der Fünften Sinfonie Beethovens erscheinen, für mich spitzt sich alles auf die Frage zu, ob mein Nachbar die Farbe Rot genauso empfindet wie ich, oder ob sich sein Erleben derselben Situation von dem meinen unterscheidet.

Weshalb man sich heute scheut, hinter du Bois-Reymonds Ignorabimus ein Ausrufezeichen zu setzen und ein Fragezeichen vorzieht, liegt auch daran, dass man immer besser erfasst, wie die Erregungsmuster im Gehirn mit den vorgefundenen Situationen zusammenhängen. Dieses wachsende Wissen scheint mir aber eher eine Seitwärtsbewegung zu sein. Es sagt uns nach wie vor nichts über das Wesen des Erlebens. Die geistigen Vorgänge sind aus ihren materiellen Bedingungen nicht zu begreifen. Das Bewusstsein bleibt rätselhaft.

Für du Bois-Reymond ist unserer Naturerkenntnis eine harte Schranke gesetzt. Das verdeutlicht er mit diesem Bild (1882, S, 38): Selbst auf der höchsten denkbaren Stufe unseres eigenen Naturerkennens gleichen unsere „Anstrengungen, über diese Schranke sich fortzuheben, einem nach dem Monde trachtenden Luftschiffer“.

Der Luftschiffer hat wenigstens den Mond vor Augen. Peter Bieri meint, dass wir nicht einmal den Sehnsuchtsort kennen (1992, S. 56): „Für das Rätsel des Bewusstseins gilt etwas, was für sonstige Rätsel nicht gilt: Wir haben keine Vorstellung davon, was als Lösung, als Verstehen zählen würde.“

Sackgassen

Jegliche Metaphysik sorgt für eine Einschränkung des Denkens. Wer seinen Denkrahmen mutwillig einengt, kommt der Lösung des Welträtsels nicht näher. Einen solchermaßen verfehlten Versuch zur Lösung des Welträtsels unternimmt der Naturalist. Er scheitert schon auf der Ebene der Logik; Erfahrungen und Fakten sind für den Nachweis seines Missgeschicks nicht vonnöten. Weiterlesen →

Veröffentlicht unter Bildungswesen, Biologie, Korrelation und Kausalität, Logik, Naturwissenschaften | Verschlagwortet mit , , , | 68 Kommentare

Wie gefährlich ist Corona?

Veröffentlicht am 18. September 2020 von Timm Grams

Im vergangenen Jahr trat die Krankheit COVID-19 neu auf. Sie wird von einem Coronavirus verursacht, genannt SARS-CoV-2. Dieses Virus hat aufgrund seiner Ausbreitungsdynamik und wegen der von ihm verursachten teils schweren Krankheitsverläufe das Leben aller Länder umgekrempelt: Hygienemaßnahmen und Isolierung bis hin zur Quarantäne legen das öffentliche Leben in Teilen zeitweise lahm. Die Grundrechte sind eingeschränkt – eine wahre Zumutung.

Aktuell sieht es in Deutschland so aus: Anfang April lag die Zahl der amtlich gemeldeten Covid-19-Fälle bei 5000 (über sieben Tage gemittelt). Auch aufgrund der anfangs strengen Isolierungs- und Hygienemaßnahmen bis hin zum Lockdown ging diese Zahl Anfang Juni zurück auf etwa 360. Seither steigt sie wieder an und liegt derzeit bei etwa 1300. Der neuerliche Anstieg der Fallzahlen lässt sich zum Teil auf die Ausweitung der Tests zurückführen. Das und auch die Tatsache, dass vermehrt junge und widerstandsfähige Leute betroffen sind, mag die Ursache dafür sein, dass die Zahl der  Todesfälle nicht in demselben Maße ansteigt wie die Fallzahlen – so berichten die Medien, beispielsweise DER SPIEGEL in Heft 37/2020.

In den Daten des Robert-Koch-Instituts kann ich zurzeit allerdings keine allzu beruhigenden Signale finden. Die Statistik der Todesfälle bricht zu früh ab, als dass die Verringerung der Kopplung von Fall- und Todeszahlen bereits sehr deutlich werden könnte.

Verunsicherung

Verschwörungstheorien

Bei uns ist die Corona-Krise bisher ganz glimpflichen verlaufen. Eine Bekannte meinte, dass es das Virus gar nicht gebe, denn „niemand hat das Virus bisher gesehen“. Ich habe ihr eine röntgenmikroskopische Aufnahme des Virus zukommen lassen.

Dieses Erlebnis hat mich aufmerken lassen. Die Krise verunsichert die Menschen, führt zum Kontrollverlust. Um die Sache für sich wieder ins Lot zu bekommen, gibt es viele Reaktionsweisen: von der Leugnung über die Verharmlosung bis hin zur Benennung von Sündenböcken. Die Verunsicherung ist der ganz reale Nährboden für allerlei Tollheiten. Verschwörungstheorien haben Konjunktur. Davon war hier schon die Rede.

Die eigene Unsicherheit ist vielleicht nicht vollständig vermeidbar, aber verringern lässt sie sich schon. Dazu muss man nicht Fachwissenschaftler sein, auch dem Laien gelingt das. Meist genügen Alltagslogik und Dreisatzrechnung. Weiterlesen →

Veröffentlicht unter Biologie, Naturwissenschaften, Statistik | Verschlagwortet mit , , | 5 Kommentare

Skepsis ohne (metaphysische) Scheuklappen

Veröffentlicht am 31. August 2020 von Timm Grams

Wir haben das Jahr 1968. Frankfurt am Main ist nah. Der Positivismusstreit in der deutschen Soziologie erregt die Studentenbewegung. Die Aktivisten positionieren sich gegen Popper. Nur wenige stehen auf seiner Seite. Ich mache gerade Vordiplom und bekomme von all dem herzlich wenig mit. Nur der Name Popper und die Rede vom Falsifikationskriterium bleiben haften. Erst etwa ein Jahrzehnt später, ich bin bereits eine geraume Zeit als Ingenieur tätig, bringt mich ein ZEIT-Aufsatz dazu, mich intensiv mit Karl Raimund Popper und seinem Werk zu beschäftigen. Ralf Dahrendorf schreibt begeistert vom „Jahrhundertwerk“ Poppers: Die offene Gesellschaft und ihre Feinde. Poppers Werk hat mich seither nicht mehr losgelassen.

Wir machen einen Sprung ins Heute. Seit fünfzehn Jahren bin ich randständiges Mitglied der Skeptikerbewegung und beobachte deren Irrungen und Wirrungen aus nächster Nähe. Die vereinsinternen Auseinandersetzungen mit den Wortführern des Vereins bringen mich darauf, mir den Positivismusstreit doch einmal genauer anzusehen. Für viel Geld erwerbe ich antiquarisch die Textsammlung. Die Investition hat sich gelohnt. (Das dtv-Bändchen von 1993 hätte damals nur 19,90 DM gekostet.)

Skeptikerbewegung

Ideologischen Verengung

Im Internet stieß ich vor mehr als fünfzehn Jahren auf den deutschen Ableger der Skeptikerbewegung, die 1976 in den USA entstanden war.

Die Selbstdarstellung des Vereins gefiel mir. Ein erfreulich bunt zusammengewürfelter Haufen schien das zu sein, der durch die Überzeugung geeint wird, „dass Wissenschaft und kritisches Denken für die gesellschaftlichen Herausforderungen von heute und morgen wichtiger sind denn je“. Vorschnelle Urteile wollten diese Leute vermeiden und stattdessen der Prüfung „mit wissenschaftlichen Methoden und den Instrumenten des kritischen Denkens“ Vorrang einräumen.

Das ist mein Verein, so dachte ich, und trat bei. Von der darauffolgenden Ernüchterung war im Hoppla!-Blog bereits ausführlich die Rede. Ich beobachtete Fehlentwicklungen. Als Hauptursache der Irrwege machte ich die ideologische Verengung auf den (ontologischen oder auch: metaphysischen) Naturalismus aus. Was darunter zu verstehen ist und zu welchen Exzessen er führte, steht im Artikel über Pseudoskeptiker.

Der Atheismus nimmt Fahrt auf

Von Anfang an waren die Führungsfiguren der Skeptikerbewegung auch säkulare Humanisten; sie verstanden sich als Atheisten. Bis etwa zur Jahrhundertwende hielten sie die Bereiche aber auseinander: hier Atheismus, dort Skeptizismus.

Zur Zeit meines Beitritts gab es einen Wechsel von einem eher gemäßigten Atheismus – für Gottes Existenz gibt es keine guten Gründe, und man kann gut sein auch ohne Gott – hin zu einer radikalen und kämpferischen Einstellung, nämlich dass Gott (wahrscheinlich) nicht existiere und dass der Agnostizismus von Übel sei.

Wegmarken des Wechsels sind die Gründung der Giordano-Bruno-Stiftung (2004), das „Manifest des evolutionären Humanismus“ von Michael Schmidt-Salomon (2006) und weitere Bücher: „Über die Natur der Dinge“ von Mario Bunge und Martin Mahner (2004) sowie „The God Delusion“ von Richard Dawkins (2006). Dieser Neue Atheismus ist missionarisch unterwegs und er unterwandert laizistische und weltanschaulich neutrale Vereine. Weiterlesen →

Veröffentlicht unter Bildungswesen, Moral und Ethik, Naturwissenschaften, Skeptizismus, Soziologie, Wissenschaft und Pseudowissenschaft | Verschlagwortet mit , , , , , , | Ein Kommentar

Pseudoskeptiker

Veröffentlicht am 30. Juli 2020 von Timm Grams

Und die, die mit ihm sind,
sind hart gegen die Ungläubigen,
doch barmherzig zueinander.
Koran, Sure 48, Vers 29

Lügengespinste werden als Wahrheit verkauft. Das gab’s schon immer. Heute geschieht das besonders wirkungsvoll über das Internet, dort, wo die klassischen Gatekeeper fehlen: die Journalisten und Moderatoren. Die Verschwörungstheoretiker mögen noch leicht zu durchschauen sein, schwerer fällt es bei den selbsternannten „Skeptikern“, die sich als Hüter der „wissenschaftlichen Wahrheit“ verstehen. Was ihnen als unwahr erscheint, wird abgelehnt.

Skeptizismus meint den Zweifel und nicht die Ablehnung. Kritiker, die einen negativen anstelle eines agnostischen Standpunkts einnehmen und die sich dennoch „Skeptiker“ nennen, greifen sich diesen Titel, allein um Vorteile daraus zu ziehen. In Wirklichkeit sind sie Pseudoskeptiker. So sieht das ein Mitbegründer und späterer Dissident der Skeptikerbewegung : MarcelloTruzzi.

Zur Einstimmung in das kulturelle Umfeld dieser Leute schauen wir uns das Vokabular an, das diese vorgeblichen Skeptiker gegen die von ihnen verachtete und bekämpfte Denkungsart einsetzen: Bullshit, Unfug, Schwachfug, Dummfug, Blödfug, Schwurbelei. Das ist Häme – nicht sehr witzig; ich habe die Wörter dem einschlägigen Blog entnommen.

Wir erkennen schon daran: Es gibt „die da drinnen“, das sind die Wahrheitsbesitzer, und „die da draußen“, denen man ihre Dummheit so recht vor Augen führen muss. Diese Einstellung geht einher mit einem makellosen Selbstbild und einem Verhalten, das dem Selbstbild krass widerspricht; auffällig ist die Aggression, die sich sowohl gegen „die da draußen“ wendet als auch gegen Dissidenten in den eigenen Reihen.

Aber gehen wir es langsam an und schön nacheinander. Ich stelle das Muster eines Vereins vor, der das Publikum über seine wahre Natur täuscht. Sie können die Schilderung für eine Karikatur oder eine Fiktion halten, wenn es Ihrem Wohlgefühl dient. Ich empfehle jedoch die skeptische Methode: genau hinsehen und prüfen. Weiterlesen →

Veröffentlicht unter Humanismus, Skeptizismus, Wissenschaft und Pseudowissenschaft | Verschlagwortet mit , | 60 Kommentare

Siebtes Intermezzo: Der Skeptiker in seiner Welt

Veröffentlicht am 30. Juli 2020 von Timm Grams

Dies ist die leicht gekürzte Fassung eines Artikels, der für die Zeitschrift skeptiker der Gesellschaft zur wissenschaftlichen Untersuchung von Parawissenschaften (GWUP) gedacht war. Er wurde abgelehnt mit den Worten: „Bei dem Text handelt es sich um die Darstellung des privaten Idealbildes eines ‚Skeptikers‘, jedoch ist unsere Zeitschrift kein Forum für derartige private Ausführungen. Selbstverständlich steht es Ihnen frei, dieses Ideal zu pflegen und den Text andernorts zu veröffentlichen.“ Der Beitrag wurde nicht etwa wegen Qualitätsmängeln abgelehnt, auch nicht wegen eines abwegigen Themas. Nein, er wurde abgelehnt, weil er eine Meinung ausdrückt, eine, die der herrschenden  offenkundig widerspricht.

Der Skeptiker schaut genau hin; er untersucht und prüft. Von den Basics für Skeptiker hatten wir es schon. Wie aber stellt er sich die Welt vor, in der er agiert? Wie weit reicht die skeptische Methode und wo hat sie ihre Grenzen? Ab wann wird Toleranz wichtig? Weiterlesen →

Veröffentlicht unter Intermezzo, Moral und Ethik, Naturwissenschaften, Skeptizismus | Verschlagwortet mit , | 6 Kommentare

Darf „Rasse“ im Grundgesetz stehen?

Veröffentlicht am 28. Juni 2020 von Timm Grams

Die Süddeutsche Zeitung berichtet am 12. Juni 2020, dass der Grünenchef Robert Habeck vorschlägt, den Begriff „Rasse“ im Grundgesetz durch die Formulierung „rassistische Zuschreibungen“ zu ersetzen.

Darum geht es: In Artikel 3 Absatz 3 des Grundgesetzes lesen wir „Niemand darf wegen seines Geschlechtes, seiner Abstammung, seiner Rasse, seiner Sprache, seiner Heimat und Herkunft, seines Glaubens, seiner religiösen oder politischen Anschauungen benachteiligt oder bevorzugt werden.“

Da fehlt es nicht an Klarheit: Rassismus wird, wie all die anderen angesprochenen Diskriminierungen, geächtet. Ebenfalls unmissverständlich ist GG Artikel 116, Absatz 2, der unter anderem die Wiedereinbürgerung von Personen regelt, die von den Nazis aus „rassischen Gründen“ ausgebürgert worden waren.

Die von Habeck gewünschte Grundgesetzänderung hätte keine inhaltlichen Konsequenzen. Wird am Grundgesetz aber ohne Not herumgedoktert, verliert es an normgebender Kraft und bekommt den Beigeschmack der Beliebigkeit. Also: Finger weg davon.

Ein Freund widerspricht. Er verweist darauf, dass Rasse ein künstlicher Begriff sei, der als ideologischer Kampfbegriff bereits unsägliches Leid über die Menschheit gebracht habe. Es gebe zwar Tierrassen, aber für die Idee der Menschenrassen gebe es keine biologische Begründung.

Was den Sachverhalt angeht, pflichte ich ihm bei. Eine Handlungsnotwendigkeit ergibt sich für mich daraus aber nicht. Wörter haben es an sich, dass sie nicht vollkommen klar definiert sind. Es gibt Leute, die verbinden mit einem bestimmten Wort einen Sinn, anderen gelingt das nicht. Für alle von Bedeutung ist das daraus abgeleitete Tun, und damit ist das Wort in der Welt – für alle.

Wer im Grundgesetz aufräumen will und dabei mit dem Wort „Rasse“ anfängt, der kann mit dem Wort „Volk“ weitermachen, oder mit „Gott“. Es gibt ein großes Betätigungsfeld.

Leider ist die Wirkung solcher Säuberungsaktionen eine andere als beabsichtigt. Die Menschen lassen sich nämlich ungern von beflissenen Eliten vorschreiben, welche Wörter sie verwenden dürfen und welche nicht. Das Aufbegehren der amerikanischen Mittelklasse gegen die „politische Korrektheit“ hat zum Aufstieg des Donald Trump beigetragen.

Wenn ich mich recht erinnere, stand vor Jahren im Café Chaos an der Hochschule Fulda eine Lampe, getragen von einem Mohr (so sagte man vor langer Zeit). Das Teil zeugt nicht von feinem Geschmack; aber besonders anstößig fand es damals auch keiner. Bis Noah Sow zu einer Lesung kam. Sie reiste sofort wieder ab. Das Angebot, das Corpus Delicti zu entfernen, konnte sie nicht beruhigen. (Das Bild hat Noah Sow anlässlich ihres Besuches gemacht.)

In ihrem Blog schreibt Frau Sow, wie empörend sie es fand, dass man in diesem Wüstenkaff namens Fulda offenbar noch nie etwas von PoC gehört habe (27. Oktober 2011).

Aus der Episode haben wir, die betroffenen Bewohner des Wüstenkaffs, durchaus etwas gelernt, nämlich dass wir uns künftig mehr Gedanken darüber machen sollten, was die Mitbürger anderer Hautfarbe, anderer Herkunft oder anderer Religion verletzten könnte. Dennoch werde ich auch künftig Schwarze genau als solche bezeichnen; sie tun es ja selbst – zu Recht voller Stolz.

Dass unsere schwarzen Freunde und Kommilitonen mit dem Begriff PoC (People of Color) etwas anfangen können, ist mir noch nicht zu Ohren gekommen. Wichtiger als solche Wortklauberei ist der tatsächlich vorhandene und auf nett geschminkte Rassismus gebildeter Kreise.

Aufgrund einer Anfrage aus meinem Skeptiker-Umfeld habe ich mich erneut mit dem Evolutionären Humanismus des Julian Huxley beschäftigt. Auf dieses Werk beruft sich die Giordano-Bruno-Stiftung in ihrem „Manifest des evolutionären Humanismus“, geschrieben von ihrem Geschäftsführer Michael Schmidt-Salomon. Im letzten Kapitel von Huxleys Buch „Evolutionary Humanism“ finden wir seine Galton Lecture Eugenics in Evolutionary Perspective. Kernsätze daraus:

“The basic fact about the races of mankind is their almost total overlap in genetic potentialities. But the most significant fact for eugenic advance is the large difference in achievement made possible by a small increase in the number of exceptional individuals.”

“Thus two racial groups might overlap over almost the whole range of genetic capacity, and yet one might be capable of considerably higher achievement, not merely because of better environmental and historical opportunity, but because it contained say 2 instead of 1 per cent of exceptionally gifted men and women.”

Kurz gesagt: Die Rassen unterscheiden sich im statistischen Mittel genetisch nicht. Das spricht gegen groben Rassismus. Den Unterschied machen die außerordentlich Begabten: Manche Rassen haben ein paar mehr davon als andere. Für mich zeugen diese Aussagen von Rassismus light. Wir sollten einmal genauer hinsehen.

Veröffentlicht unter Bildungswesen, Biologie, Humanismus, Moral und Ethik | Verschlagwortet mit , | 34 Kommentare

Klüger irren – Denkfallen vermeiden mit System. 2. Auflage

Veröffentlicht am 14. Mai 2020 von Timm Grams

Kurz entschlossen — danebengehauen…Vorher nachdenken, nachmessen oder kalkulieren wäre wohl besser gewesen! Dieses Buch hilft Ihnen, Ihre Denkmechanismen zu erkunden und zu verbessern. Fehler und Zufall treiben den Fortschritt an. So entsteht das Neue. Wer es sehen will, braucht Wissen und die Fähigkeit, überraschende Beobachtungen richtig einzuordnen.

Es ist jedoch kein Erfolgsrezept, die alten Fehler wieder und wieder zu machen. Lernen Sie aus Ihren Reinfällen und denjenigen der anderen.

Weniges wird uns bewusst. Denkmechanismen wirken meist im Verborgenen, ungefragt und blitzschnell. Sie sind bewährt, manchmal aber auch verkehrt. Optische und kognitive Täuschungen, irreführende Statistiken, Paradoxien, Manipulationsversuche lauern überall. Viele Irrwege lassen sich durch den Einsatz von etwas Logik und Mathematik vermeiden.

Lernen Sie, wie Sie Warnzeichen erkennen und richtig deuten können, wie weit das von Ihnen oft und meist unbewusst genutzte Indifferenzprinzip trägt, welche Rolle Analogien bei der Entstehung des Neuen spielen und wann Sie gefahrlos verallgemeinern dürfen.

2., überarbeitete und erweiterte Auflage.

Vorwort zur zweiten  Auflage

„Klüger irren“ soll nicht nur ein nettes Wortspiel sein. Gemeint ist eine skeptische Grundhaltung, die ich in der zweiten Auflage deutlicher herausstelle. Das Ziegenproblem hat eine Konzentration auf das Wesentliche gut vertragen. Das schafft Platz für das Dornröschenproblem, das einen noch interessanteren Disput nach sich gezogen hat. Zusätzlich hineingenommen habe ich die Risikobewertung, die beispielsweise die Frage „Impfen ja oder nein“ zu beantworten hilft. Anstatt die Esoterik an der heute sichtbaren – und nicht  einmal persiflierbaren – Oberfläche zu packen, nehme ich mir die tieferen Wurzeln dieses alten Denkens vor; Wundererfahrungen und magische Deutungen sind auch spirituell Unbegabten einen zweiten Gedanken wert.

Veröffentlicht unter Bildungswesen, Moral und Ethik, Naturwissenschaften, Problemlösen, Skeptizismus, Statistik, Wahrscheinlichkeitsrechnung, Wissenschaft und Pseudowissenschaft | Verschlagwortet mit , , , , , , , , , | 2 Kommentare