Die Unterwanderungsstrategie des Neuen Atheismus

Veröffentlicht am 4. Juni 2015 von Timm Grams

Dies ist ein Fallbericht. Er zeigt, wie der Neue Atheismus (GBS, Brights) weltanschaulich pluralistische oder neutrale Vereine und Verbände mit säkular-laizistischer Grundhaltung (GWUP, HVD) unterwandert und dabei totalitäre Strukturen aufbaut. Das habe ich erst in den letzten Wochen klar erkannt, obwohl ich durch den Spiegel-Artikel Der Kreuzzug der Gottlosen von 2007 hätte vorgewarnt sein müssen. Aber ich habe den Ausriss erst jetzt, anlässlich der Recherchen, in meinem Exemplar des Richard-Dawkins-Werkes „The God Delusion“ wiederentdeckt.

Die GWUP öffnet sich der atheistischen Mission

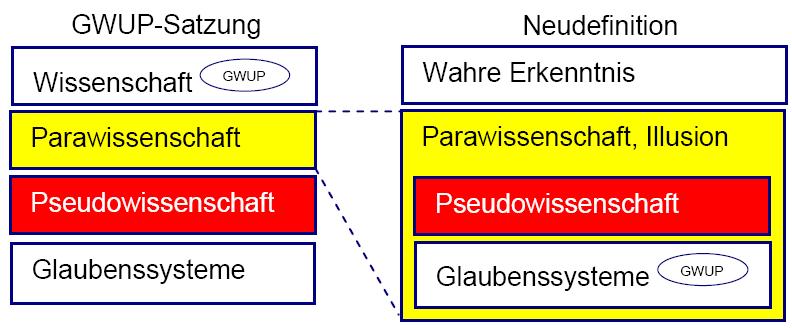
Eine offizielle Informationsschrift der Gesellschaft zur wissenschaftlichen Untersuchung von Parawissenschaften (GWUP) hat den Titel „Parawissenschaft – Pseudowissenschaft“ (Martin Mahner, 5.1.2010). Sie steht im Widerspruch zur gültigen GWUP-Satzung.

Es geht um eine Ausweitung des Arbeitsfeldes der GWUP. Die entscheidende Grenze für die GWUP soll danach nicht länger zwischen Wissenschaft und Nichtwissenschaft verlaufen, sondern zwischen Erkenntnis und Illusion (Martin Mahner in „Was sind Parawissenschaften?“, skeptiker 4/2009, S. 186-190). Auch Metaphysik und Religionen sollen demnach in das Zielgebiet der GWUP fallen.

Auf der Mitgliederversammlung 2014 in München (traditionell am Freitag nach Himmelfahrt) stellte ich einen Antrag, in dem der Vorstand aufgefordert wird, die Widersprüche zwischen offiziellen Verlautbarungen und Satzung zu beseitigen und insbesondere die Neudefinition „Parawissenschaft – Pseudowissenschaft“ zurückzuziehen.

In der Versammlung wurde der Wunsch nach einer gründlichen Diskussion laut. Die Entscheidung wurde auf das Folgejahr vertagt, also auf Himmelfahrt 2015.

In diesem Jahr, am Freitag nach Himmelfahrt, lag der Mitgliederversammlung ein Beschlussvorschlag des Vorstands zu einer Satzungsänderung vor. Dieser bezweckt eine Ausweitung und Aufweichung des Vereinszwecks derart, dass die GWUP-Informationsschrift und die Ausweitung des GWUP-Arbeitsfeldes nun satzungskonform sind. In der Begründung dieses Antrags spielte die von mir kritisierte Informationsschrift keine Rolle, stattdessen wurden ein paar, im Grunde haltlose, Argumente vorgeschoben. Es ging also nicht mehr darum, sich nach der Satzung zu richten, sondern darum, die Satzung so zu ändern, dass die Informationsschrift dann satzungskonform ist.

Die Möglichkeit, neben der Esoterik auch die Religionen aufs Korn zu nehmen, wird damit ausdrücklich eröffnet. Offenbar besteht die Absicht, die GWUP zu einer Einrichtung der atheistischen Missionierung umzubauen.

Giordano-Bruno-Stiftung und Brights

Zweifel an dieser Zielsetzung verfliegen, wenn man sich das Personal, die in prominenter Stellung Handelnden, ansieht. Es folgt ein Auszug aus der Besetzungsliste.

Martin Mahner, Verfasser der GWUP-Informationsschriften, ist Hausphilosoph der GWUP und zugleich Beirat der Giordano-Bruno-Stiftung (GBS). Amardeo Sarma, Vorsitzender der GWUP, gibt sich als Mitglied der GBS zu erkennen. Viele Anhänger der GBS sind gleichzeitig Anhänger oder Mitglieder der Brights.

Eine Schlüsselfigur des noch zu schildernden einjährigen „Diskussionsprozesses“ von Himmelfahrt 2014 bis Himmelfahrt 2015 ist Rainer Wolf. Er ist sowohl Mitglied im Vorstand und dort zugleich Repräsentant des Wissenschaftsrats der GWUP als auch Mitglied der Brights. Rainer Rosenzweig, ehemals Doktorand von Rainer Wolf, ist Mitglied im Wissenschaftsrat der GWUP und im Beirat der GBS.

Die GBS als auch die Brights missionieren aggressiv für den Neuen Atheismus in der Gefolgschaft von Richard Dawkins („The God Delusion“, 2006). Die Ziele und Methoden dieser Vereinigungen sind mit den Grundsätzen eines weltanschaulichen Pluralismus unverträglich. Im Hoppla!-Artikel „Die Giordano-Bruno-Stiftung (GBS): nur wirr oder gar gefährlich?“ habe ich ein paar Bemerkungen dazu gemacht.

Das Büchlein „Manifest des evolutionären Humanismus“ von Michael Schmidt-Salomon aus dem Jahre 2005 bildet die „philosophische“ Grundlage der GBS. Die Absicht dahinter wird schnell klar: Jeder liberale Geist soll sich darin irgendwo wiederfinden können. Nur nachdenken darf er dabei nicht. Der Text ist, wie der ihm zugrundeliegende ontologische Naturalismus mahnerscher Prägung, von haarsträubender Oberflächlichkeit. Dazu strotzt er vor inneren Widersprüchen. Hier nur zwei weitere Beispiele.

Erstens: Der auf Seite 37 angesprochene Falsifikationismus des Karl Raimund Popper ist eng verbunden mit dessen „Sozialtechnik der Einzelprobleme“ (aus: „Die offene Gesellschaft und ihre Feinde“). Das großsprecherische 10. (An‑)Gebot des Evolutionären Humanismus auf  S. 158 steht im unversöhnbaren Gegensatz dazu: „Stelle Dein Leben in den Dienst einer ‚größeren Sache‘“. Aus diesem Satz spricht Totalitarismus, also das Ziel, „ein umfassendes neues Wertsystem durchzusetzen“ (Brockhaus). Nichts lag Popper ferner.

Zweitens: Auf S. 94 wird der naturalistische Fehlschluss angesprochen, nach dem man das Sollen, das sind die moralischen Gesetze, aus dem Sein, den Naturgesetzen also, herleiten könne. Obwohl das Scheitern dieses Programms zugestanden wird, versucht Schmidt-Salomon einige Seiten später (S. 120 ff.) genau das: Die Etablierung einer humanistischen Ethik auf der Basis von Vernunft und Naturverständnis. Der Präferenzutilitarismus des Peter Singer wird geradezu als Denknotwendigkeit angeboten.

Kürzlich wurde selbst Schmidt-Salomon ob der Wahl des Peter Singer zur Leitfigur  unheimlich zumute.

Für Joachim Kahl vom HVD sind die zehn Angebote des evolutionären Humanismus ein Türöffner der Beliebigkeit (Fürther Streitgespräch vom 27.06.2006). Allmählich spricht sich herum, wie dürftig das Angebot des evolutionären Humanismus der GBS ist.

Missionsgebiete: GWUP und HVD

Weltanschaulich pluralistische und eher dem Diesseits zugewandte Vereinigungen wie der Humanistische Verband Deutschlands (HVD) und die Gesellschaft zur wissenschaftlichen Untersuchung von Parawissenschaften (GWUP), die gut ohne derartige Metaphysik auskommen, gehören zum Missionsgebiet der Neuen Atheisten. Auch wenn der HVD eine säkular-laizistische Gesellschaft zum Ziel hat und den politische Einfluss der Kirchen zurückdrängen will, heißt das noch lange nicht, dass in die dann vermeintlich entstehende Lücke eine andere Religion, eine in der Gestalt des Neuen Atheismus, hineingestopft werden muss.

Der zunehmende Einfluss der Neuen Atheisten auf den HVD wird ersichtlich, wenn man das 2011  verfasste „Humanistische Selbstverständnis“ des HVD mit den im Jahr darauf publizierten „Humanistischen Grundsätzen“ des HVD Bayern vergleicht: Das erstgenannte Papier ist weitgehend frei vom ideologischen Gedankengut der Neuen Atheisten. In dem zweiten verrät sich deren Einfluss durch typischen Naturalisten-Sprech: „Es geht überall mit rechten Dingen zu“, „Humanisten sind Naturalisten“ und dergleichen mehr.

Einen Großteil des Einflusses erreichen die neuen Atheisten durch Personalunion. Im Falle der GWUP leisten das die Herren Sarma, Mahner, Rosenzweig und Wolf. Dazu kommen die Philosophen Gerhard Vollmer und Bernulf Kanitscheider, die sowohl Mitglieder des GWUP-Wissenschaftsrats als auch des GBS-Beirats sind. Das sind nur die Personen, deren Zugehörigkeiten ich zweifelsfrei kenne.

Die GWUP-interne „Diskussion“ zur Satzungsänderung zeigt, wie die Neuen Atheisten ihren Einflussbereich ausweiten. Mit offenen, wissenschaftsorientierten Diskussionen hat das nichts zu tun. Es läuft nach dem Motto: Wir sind die Aufgeklärten, die Brights, wir haben Recht, und deshalb heiligt der Zweck die Mittel.

Um bereits jetzt unangebrachten Vorwürfen zu begegnen: Auf den monatlichen Treffen der Würzburger GWUPler habe ich immer wieder betont: Mein Untersuchungsgegenstand ist nicht die Homöopathie, auch nicht Astrologie oder Wünschelrutengängerei; mein Interesse gilt seit einiger Zeit der GWUP, ihren inneren Strukturen und ihrer Diskussionskultur.

Eine „Diskussion“ mit Glaubenskämpfern

Ein Jahr lang, von Himmelfahrt 2014 bis Himmelfahrt 2015, fand eine bemerkenswerte „Diskussion“ zum Thema Satzungsänderung statt. Sie ist wesentlich durch die  totalitäre Grundhaltung der GBS-Leute innerhalb der GWUP geprägt.

In diesem Diskussionsprozess nahm ich einige Demütigungen in Kauf, denn ich hatte ein Ziel vor Augen, nämlich den Strukturen der GWUP näher zu kommen. Ich stelle ein paar Wesenszüge des Prozesses heraus. Eine Schlüsselfigur ist Rainer Wolf.

1. Kompromisslosigkeit. Sie ist eine Eigenschaft aller Glaubenskämpfer und kommt hier nicht überraschend. Der harte und nicht anzweifelbare Glaubenskern wird durch ein gefälliges Drumherum versüßt. Man darf sich durch die verbalen Schleifchen nicht täuschen lassen: „Deine kritischen Überlegungen kann ich sehr gut nachvollziehen, und ich glaube, sie treffen ganz Wesentliches. Drei Punkte sehe ich, wo ich wohl etwas anders denke …“ Oder so: „Auch wenn ich nicht allen Formulierungen von Michael Schmidt-Salomon  zustimme, ist er doch einer der wenigen Philosophen …“ Oder so: „Wir schließen die Festlegung auf eine Weltanschauung aus“ und gleichzeitig wird alles getan, um genau eine solche Festlegung zu ermöglichen. Ein Diskurs kommt aufgrund der Ablenkung durch Strohmann- und Stellvertreter-Argumente erst gar nicht zustande.

2. Intransparenz. Mir war zu keinem Zeitpunkt klar, mit welchen Personen (Wissenschaftsrat? Vorstand?) ich es zu tun hatte und wie der Konsens unter ihnen zustande gekommen sein könnte.

3. Totalkontrolle. Einem Hinweis vom 01.08.2014 entnehme ich, dass die Lenkung der Meinungsbildung einer „kleinen Kommission“, bestehend aus Rainer Rosenzweig, Martin Mahner und Rainer Wolf übergeben worden war. So funktioniert das totalitäre Regime: Es gibt eine Kommission der Eingeweihten, in diesem Falle alles Neuatheisten; ihnen gegenüber sitzt der Delinquent, in dem Fall ich. Warum ich auf so etwas allergisch reagiere, kann man in meiner Abschiedsvorlesung im Zusammenhang mit der „Entnazifizierung eines Achtjährigen“ nachlesen.

4. Bevormundung. Manche meiner E-Mails wurden von Rainer Wolf einfach zurückgehalten. Auf Nachfrage gab er mir den Bescheid, dass damit Porzellan zerschlagen würde. Andere E-Mails wurden von Rainer Wolf mit Kommentaren versehen und erst dann an den internen Zirkel weitergeleitet. Ein Leserbrief zu einem Mahneraufsatz im skeptiker hat die Redaktion wohl erst gar nicht erreicht. Anstelle einer Eingangsbestätigung erhalte ich nur Wolfs Kommentar: „Dem Inhalt Deines Leserbriefs kann ich beim besten Willen nicht zustimmen“ (Wolf, 21.12.2014). Und das war’s dann.

5. Gutsherrenart. Mein mehrfach geäußerter Wunsch, meinen Gegenantrag genauso wie den Vorstandsantrag vorab an alle Mitglieder zu verteilen, aus Kostengründen nur per E-Mail, wurde abgelehnt mit den Worten: „Der Vorstand hat bereits nach eingehender Diskussion vor mehr als eine Woche beschlossen, Ihr Schreiben nicht per reguläre Post an alle Mitglieder zu verschicken“ (Sarma, 14.04.2015). Meine Versuche, die Mitgliedschaft doch noch direkt zu erreichen, wurden dadurch vereitelt, dass mir tote Geleise gewiesen wurden, wie beispielsweise eine vermeintliche Mailingliste der Mitglieder (Sarma, 09.04.2015). Ich musste erst mühsam lernen, dass es sich dabei um ein fluktuierendes Forum handelt, an dem immer nur wenige Mitglieder teilnehmen.

6. Autoritätsargumente. Fremde Ideen muss man schnell wieder loswerden. Wie das funktioniert? Man setzt auf das Autoritätsargument und auf Einschüchterung: „Mir liegt mittlerweile die Rückmeldung vor, dass alle Wissenschaftsräte sich einstimmig für die neue Satzung ausgesprochen haben“ (Rainer Wolf am 12.05.2015).

Ein Teilnehmer der Mitgliederversammlung 2015 kritisierte das starre Verhalten des Vorstands und empfahl, sich doch besser an dem bekannten Ausspruch zu orientieren: „Ich bin zwar anderer Meinung als Sie, aber ich würde mein Leben dafür geben, dass Sie Ihre Meinung frei aussprechen dürfen.“

Abschluss des Verfahrens

Angesichts des massiven Auftretens des Vorstands für die Satzungsänderung war mir die Chancenlosigkeit meines Widerstands seit Monaten klar. Aber ich wollte ja sehen, wie die Sache abläuft. Bis zum bitteren Ende. Immerhin gab es ein paar Mitglieder, die dem Vorstand, trotz dessen massiven Auftretens, nicht  gefolgt sind. Mutig.

Nachdem der Vorstandsvorschlag von der Versammlung mehrheitlich angenommen war, gab ich eine Erklärung zu Protokoll. Darin wiederholte ich meine bereits vor einem Jahr geäußerte Auffassung, dass einem solchen Beschluss, der eine wesentliche Zweckänderung des Vereins nach sich ziehe,  alle Vereinsmitglieder, ob anwesend oder nicht, zustimmen müssten. Unter diesen Bedingungen müsse der Vorstandsantrag als gescheitert gelten. Diese Stellungnahme sollte dem Amtsrichter in Darmstadt, der über die Satzungsänderung zu befinden hat, vorgelegt werden.

Daraufhin gab das Vorstandsmitglied Ralf Neugebauer, Richter am OLG Düsseldorf, zu verstehen: Das sei alles mit dem Amtsrichter vorab geklärt worden.

Auch dahinter könnte man Ungeheuerliches vermuten. Vorsichtshalber habe ich im Anschluss an die Mitgliederversammlung meine Erklärung dem Amtsgericht direkt zugeschickt. Mal sehen, was daraus wird.

Meine Erfahrung zusammengefasst: Wer sich mit den Brights oder den Vertretern der  Giordano-Bruno-Stiftung anlegt, der bekommt es mit Feinden der offenen Gesellschaft zu tun.

Veröffentlicht unter Naturwissenschaften, Skeptizismus, Wissenschaft und Pseudowissenschaft | Verschlagwortet mit , , , | 6 Kommentare

Die Giordano-Bruno-Stiftung (GBS): nur wirr oder gar gefährlich?

Veröffentlicht am 11. Mai 2015 von Timm Grams

Die Giordano-Bruno-Stiftung vertritt nach eigener Auskunft „die Position des ‚Evolutionären Humanismus‘, die Mitte des letzten Jahrhunderts von dem bedeutenden Evolutionsbiologen und ersten Generaldirektor der UNESCO, Julian Huxley, formuliert wurde“.

In dem vom Geschäftsführer der GBS Michael Schmidt-Salomon verfassten Manifest des evolutionären Humanismus (erschienen 2005 im einschlägig tätigen Alibri-Verlag) steht der Hinweis auf die philosophischen Grundlagen der Stiftung: „Evolutionäre Humanisten vertreten ein dezidiert naturalistisches Weltbild. Das heißt: Sie gehen von einem Bild des Kosmos aus, in dem ‚alles mit rechten Dingen‘ zugeht.“ Dabei verweist Schmidt-Salomon auf das Werk „Über die Natur der Dinge“ von Mario Bunge und Martin Mahner. Auch der Hinweis auf die Übernatur, bevölkert von Göttern, Dämonen, Hexen und Kobolden, fehlt nicht.

Man will sich also an der Wissenschaft orientieren. Esoterik, Mystizismus, metaphysisches Gedankengut und ganz besonders die Religionen sind es, die es zu bekämpfen gilt. Diese Intention der Stiftung wird durch das 1. (An-)Gebot des evolutionären Humanismus Schmidt-Salomonscher Prägung klar gemacht: „Diene weder fremden noch heimischen ‚Göttern‘ (die bei genauer Betrachtung nichts weiter als naive Primatenhirn-Konstruktionen sind), sondern dem großen Ideal der Ethik, das Leid der Welt zu mindern! Diejenigen, die behaupteten, besonders nah bei ‚Gott‘ zu sein, waren meist jene, die dem Wohl und Wehe der realen Menschen besonders fern standen. Beteilige dich nicht an diesem Trauerspiel! Wer Wissenschaft, Philosophie und Kunst besitzt, braucht keine Religion!“

Aber hoppla! Hier wird doch der Atheismus zur neuen Religion erhoben und auch über den Namensgeber Giordano Bruno haben wir doch etwas ganz anderes gehört und gelesen, als hier unterstellt wird.

Giordano Bruno – Märtyrer der Wissenschaft?

Warum gerade Giordano Bruno und nicht Galileo Galilei? Für eine kämpferische Glaubensgemeinschaft wie die GBS ist Galilei einfach nicht Märtyrer genug! Die Autoren Lawrence S. Lerner und Edward A. Gosselin schreiben in ihrem Aufsatz „Galileo Galilei und der Schatten des Giordano Bruno“: „Galileo ist eine schlechte Besetzung für Heldenrollen“ (Spektr. d. Wiss. 1/1987, S. 102-113).

Und da kommt dieser Vorgänger Galileis, Giordano Bruno, ins Spiel. Einer, der auf dem Scheiterhaufen der Inquisition landete. Dieser Mann macht sich als Märtyrer wesentlich besser. In der Begeisterung für diesen Helden des kopernikanischen  Weltsystems wurde wohl übersehen, dass mit Giordano ein ausgemachter Mystiker zum Helden erwählt wurde: „Giordano versteht das kopernikanische Modell des Sonnensystems falsch“ (Lerner/Gosselin). Und weiter: „Der Wert des kopernikanischen Systems liegt für Giordano Bruno nicht in seinen astronomischen Einzelheiten, sondern in den Möglichkeiten, die es als poetisches und metaphorisches Medium für weitergehende philosophische Spekulationen bietet.“

Giordano Bruno bezieht sich, ebenso wie die heutigen Esoteriker, auf die okkult-esoterische Offenbarungs- und Geheimlehre des sagenhaften Hermes Trismegistos. Was Bruno in Schwierigkeiten brachte, war weniger sein Eintreten für das kopernikanische Weltbild, sondern eher sein Bekehrungseifer im Dienste einer hermetischen Mystik, die sich auf neuplatonische Schriften des 2. und 3. Jahrhunderts berief.

Die Naturalisten stehen in Gegnerschaft zum Mystizismus. Als Vorzeigegestalt des Naturalismus ist Giordano Bruno jedenfalls denkbar ungeeignet. Was die GBS anrichtet, ist wirres Zeug.

Sehr interessant finde ich die personelle Besetzung des GBS-Kuratoriums: Zum Vorstand gehört Dr. Michael Schmidt-Salomon. Im Leitbild der Stiftung steht: „Im Auftrag der Stiftung wurden Huxleys Ideen u.a. im ‚Manifest des evolutionären Humanismus‘ wieder aufgegriffen und auf den Stand der heutigen Forschung gebracht.“ Hier hat also jemand sich selbst einen Auftrag erteilt. Ich erkenne eine Grundfigur wieder, die in diesen Naturalisten-Kreisen hohe Wertschätzung genießt: Selbstüberhöhung durch Zirkelbezug bei gleichzeitiger Immunisierung gegen fremdes Gedankengut.

Im Stiftungsbeirat finden wir einige uns bereits vertraute Personen: Bernulf Kanitscheider, Gerhard Vollmer und Martin Mahner. Sie sind eingefleischte Atheisten und sie fühlen sich in der GBS sicherlich gut aufgehoben. Warum diese Leute, nachdem sie in der  GBS ein lohnendes Tätigkeitsfeld gefunden haben, auch noch die rein wissenschaftsorientierte GWUP auf Linie bringen wollen, bleibt mir ein Rätsel.

Julian Huxley und Eugenik

Da sich die GBS auf Julian Huxley als Namensgeber des Evolutionären Humanismus beruft, sollte sich die Stiftung in Julian-Huxley-Stiftung (JHS) umbenennen. Allerdings bekäme die Stiftung dann ein Problem: Sie müsste sich wortreich von Huxleys Eugenik („Eugenics in Evolutionary Perspective“) distanzieren. Schauen wir uns ein paar Zeilen aus Huxleys Werk „Evolutionary Humanism“, 1964, an.

Die Menschheit sei unvollkommen, meint Huxley, und das in zunehmendem Maße, wenn wir nicht dagegen steuerten. Letzteres gelinge, wenn erst einmal klar sei, was den genetischen Verfall verursacht und indem man fehlerhafte und minderwertige Typen davon abbringe, sich zu vermehren. („The obverse of Man’s actual and potential further defectiveness is the vast extent of his possible future improvement. To effect this, he must first of all check the processes making for genetic deterioration. This means reducing man-made radiation to a minimum, discouraging genetically defective or inferior types from breeding, reducing human overmultiplication in general and the high differential fertility  of various regions, nations and classes in particular.“)

Solcherart Auslese brauche Verhütungs- und Sterilisierungsmethoden in Kombination mit künstlicher Befruchtung oder anderen  Methoden stellvertretender Elternschaft.  („The implementation of negative eugenics […] in practice  will depend on the use of methods of contraception or sterilization, combined where possible with A.I.D. (artificial insemination by donor) or other methods of vicarious parenthood.“)

Es sei zwingend, das genetische Niveau des Menschen hinsichtlich der geistigen und handwerklichen Fähigkeiten anzuheben. In der Praxis lasse sich das wohl mittels künstlicher Befruchtung durch ausgewählte Spender erreichen. (We „must rely increasingly on raising the genetic level of man’s intellectual and practical abilities […] Artificial insemination by selected donors could bring about such a result in practice“.)

Nur insoweit, als diese Überzeugungen auf wissenschaftlichem und überprüftem Wissen beruhen, seien sie geeignet, die menschliche Evolution in die gewünschte Richtung zu lenken. („Only in so far, as those purposes and beliefs are grounded on scientific and tested knowledge, will they serve to steer human evolution in a desirable direction.“)

Wem jetzt noch nicht schlecht geworden ist, der kann sich ja das letzte Kapitel von Huxleys Buch reinziehen.

Der Zweck heiligt die Mittel

Mit dem Satz „Der Zweck heiligt die Mittel“ hat man schon manche Schandtat gerechtfertigt. Folter scheint erlaubt. Der Totalitarismus ist nicht weit. Aber auch der evolutionäre Humanismus hat da einiges zu bieten. Fündig wird man im 4. (An-)Gebot des evolutionären Humanismus: „Du sollst nicht lügen, betrügen, stehlen, töten – es sei denn, es gibt im Notfall keine anderen Möglichkeiten, die Ideale der Humanität durchzusetzen.“

Mich irritiert, dass hier keine Einschränkung gemacht wird. Nur ein paar Beispiele werden genannt: Lügen zugunsten verfolgter Juden und der Tyrannenmord seien erlaubt. Jedoch geht es um etwas anderes, es geht um die „Ideale des Humanismus“ ganz allgemein. Nun tauchen ein paar ganz zentrale Fragen auf: Wer formuliert den Kanon der humanistischen Ideale? Wer soll ihn durchsetzen? Und vor allem: Wie soll das geschehen? Auch mit Lug und Trug?

In welche Zwickmühlen man bei diesem Vorhaben geraten kann, ist den Äußerungen selbsternannter Humanisten zu entnehmen. Peter Singer ist ein solcher. Er hat im Jahr 2011 als einer der Ersten den von der GBS verliehenen Ethikpreis der GBS erhalten.

Utilitarismus

Um der Geisteshaltung des Peter Singer, eine Spielart des Utilitarismus, etwas näher zu kommen, zitiere ich aus einem SPIEGEL-Interview mit der Überschrift „Nicht alles Leben ist heilig“. Kommentieren kann ich das Interview nicht; das würde mich überfordern. Eins zumindest – so meine ich – wird dennoch klar: Die ethischen Normen sollten niemals Angelegenheit nur einer gesellschaftlichen Gruppierung oder nur einer Weltanschauungsgemeinschaft sein.

SPIEGEL: Schon einmal, in der Aufklärung, gab es den Versuch, eine Weltsicht auf die Vernunft zu gründen. Aber damals setzten die Philosophen, anders als Sie, die Würde des Menschen an den Anfang all ihrer Überlegungen.

Singer: Es stimmt, Sie finden diesen Gedanken Ende des 18. Jahrhunderts in der Erklärung der Menschenrechte. Aber nehmen Sie zum Beispiel Kant: Er sagt, der Mensch sei stets als „Zweck an sich selbst“ zu betrachten. Doch wenn Sie sich seine Argumentation genauer ansehen, dann stellen Sie fest, dass er sich auf die Fähigkeit zu Vernunft und Autonomie beruft. Dieser Gedanke ist dann missbraucht worden, um allen menschlichen Wesen diesen Status zuzusprechen – obwohl es keine 30 Sekunden Nachdenken braucht, um sich klar zu machen, dass es durchaus menschliche Wesen gibt, die weder vernunftbegabt noch autonom sind.

SPIEGEL: Lassen Sie uns versuchen, Ihr Denkmodell auf Embryonen anzuwenden. Zunächst: Wann beginnt in Ihren Augen menschliches Leben?

Singer: Darüber gibt es unterschiedliche Meinungen – aber unter ethischem Gesichtspunkt ist es gar nicht furchtbar wichtig, für welche davon man sich entscheidet.

SPIEGEL: Nein? Über keine Frage wird in der gegenwärtigen Debatte um embryonale Stammzellen so erbittert gestritten wie über diese.

Singer: Das ist eben falsch. Moralisch wichtig ist doch nicht, ob ein Embryo menschliches Leben ist, sondern einzig die Frage, welche Fähigkeiten und Eigenschaften er hat. Denn auf diese gründet sich sein moralischer Status.

SPIEGEL: Ein früher Embryo hat aber kaum höhere Fähigkeiten als ein Bakterium oder, sagen wir, eine Kartoffelpflanze. Also steht er mit ihnen auf einer moralischen Stufe?

Singer: Der Unterschied besteht aber darin, dass der Embryo leibliche Eltern hat, denen dieser Embryo etwas bedeuten könnte. Und die hat eine Kartoffelpflanze nicht.

SPIEGEL: Solange aber diese Eltern damit einverstanden wären, könnte man diesen Embryo für jeden beliebigen Zweck verwenden – selbst wenn man Embryos zu einer Schönheitscreme oder einem Potenzmittel verarbeiten wollte?

Singer: Ein ethisches Problem hätte ich damit nicht

[…]

SPIEGEL: Wann wachsen dem Embryo denn, nach Ihrer Auffassung, erstmals irgendwelche Rechte zu?

Singer: Ein wesentlicher Punkt ist das Einsetzen von Schmerzempfinden. Ab diesem Zeitpunkt verdient der Embryo einen gewissen Schutz – ähnlich wie ihn ein Tier auch verdient.

SPIEGEL: Das heißt: Vorher gleicht der Embryo, ethisch betrachtet, einer Kartoffel, nun steigt er auf zum moralischen Wert einer Ratte?

Singer: Was den Embryo selbst betrifft, würde ich die Frage mit „Ja“ beantworten – allerdings mit der Einschränkung, dass es, wie schon gesagt, eine Sicht der Eltern gibt, die es zu berücksichtigen gilt.

[…]

SPIEGEL: Sie koppeln also das Lebensrecht, das höchste aller menschlichen Rechte, an einen Zeitpunkt, den Sie allenfalls sehr vage benennen können?

[…]

Singer: Ich habe einmal den Vorschlag gemacht, eine Phase von 28 Tagen nach der Geburt festzusetzen, nach der dann das volle Lebensrecht erst in Kraft tritt. Das ist zwar ein sehr willkürlicher Zeitpunkt, den wir einer Idee aus dem antiken Griechenland entlehnt haben. Aber es würde den Eltern Zeit für ihre Entscheidungen geben.

[…]

SPIEGEL: Bisher haben wir weitgehend über gesunde Babys gesprochen. Wie aber steht es mit schwer behinderten Babys, die möglicherweise nie volles Bewusstsein ihrer selbst erlangen werden. Kommen die nie im Laufe ihres Lebens in den Genuss eines vollwertigen Rechts zu leben?

Singer: In derartigen Fällen bin ich der Auffassung, dass sie selbst kein derartiges Recht haben. Aber sie können Eltern haben, denen sie etwas bedeuten, die ihnen Liebe geben und die sich um sie kümmern.

Veröffentlicht unter Naturwissenschaften, Skeptizismus, Spiritualität, Wissenschaft und Pseudowissenschaft | Verschlagwortet mit , , , | 75 Kommentare

„Viel hilft viel“ oder „Weniger ist mehr“?

Veröffentlicht am 19. Februar 2015 von Timm Grams

 

Hier geht es ein wenig „mathematischer“ zu als in den vorhergehenden Artikeln. Gleichzeitig nähere ich mich wieder mehr den Leitlinien dieses Weblogbuchs, in dem es darum gehen soll, Stolpersteine oder Denkfallen aufzugreifen, die uns im Alltag und in den Medien begegnen. Diesmal hab ich mir den Stolperstein selbst hingelegt und ihn vorübergehend aus dem Auge verloren.

Für die Lehrveranstaltung Problemlösen hatte ich die Denksportaufgabe „Wie viele Taxis?“ ausgegeben. Aus einer Menge von Beobachtungen war eine Schätzung für Anzahl der Taxis in einer Stadt abzuleiten. Der ersten Eingebung folgend, denkt man sich: Je mehr der Informationen ich benutze, desto genauer wird mein Schätzwert wohl werden. Aber Hoppla! Das stimmt nicht.

Die Aufgabe ist ein schönes Beispiel für die von Gerd Gigerenzer wärmstens empfohlene Weniger-ist-mehr-Heuristik. Im Artikel Bauchgefühle: Je dümmer, desto klüger? und danach in Kopf oder Bauch? habe ich die Grenzen dieser Heuristik deutlich gemacht und gezeigt, dass sie mit Bauchgefühlen recht wenig zu tun hat und eher dem „langsamen Denken auf kurzen Wegen“ zugeordnet werden muss.

Das Taxi-Beispiel gibt sehr eingängige Hinweise darauf, wann diese Heuristik hilfreich sein kann. Die Anregung  zur Taxi-Aufgabe habe ich vom Büchlein „Mathematisches Sammelsurium“ von Christian Hesse, München 2012.

Wie viele Taxis? Nehmen wir an, Sie sitzen etwas gelangweilt in einem Café und notieren sich die Nummern der vorbeifahrenden Taxis: 477, 491, 342, 596, 68, 251, 258, 917, 775, 954, 160, 875, 618, 74, 457, 100, 181, 628, 512 und 729. Sie fragen sich nun, wie viele Taxis es in der Stadt wohl gibt.

Um überhaupt zu einer mathematisch lösbaren Aufgabe zu kommen, brauchen wir ein paar Annahmen:

  1. Die Taxis der Stadt sind von 1 bis zu einer Zahl N lückenlos durchnummeriert.
  2. Die Auswahl geschieht rein zufällig: Jede der Nummern von 1 bis N erscheint also mit derselben Wahrscheinlichkeit vor dem Fenster des Cafés.
  3. Jedes mehrfach erscheinende Taxi wird nur einmal erfasst. Für den Statistiker ist das ein Urnenmodell ohne Zurücklegen.

Wir sind also an einer Schätzung des uns unbekannten Wertes N interessiert. Mit a will ich die kleinste der beobachteten Taxinummern bezeichnen und mit b die größte. Die Zahl der insgesamt beobachteten Taxis ist n, hier gleich 20.

Dass die Nummer b = 954 bereits die größte der Nummern und damit gleich der Anzahl der Taxis ist, dass also b = N gilt, ist ziemlich unwahrscheinlich. Zur besseren Abschätzung des Wertes N schlage ich Ihnen die Formel b*(n+1)/n – 1 vor. Das gäbe im vorliegenden Fall den Wert 1001.

Auf diese Formel bin ich durch die Analogie-Heuristik gekommen: Habe ich Ähnliches schon einmal gesehen? Kenne ich ein verwandtes Problem?

In der Tat hat das Taxi-Problem eine gewisse Ähnlichkeit mit dem Problem „Das erste Ass“ aus meiner Problemsammlung Querbeet. Jetzt geht es nur noch darum, den dort beschriebenen Lösungsvorschlag auf das Taxi-Problem zu übertragen. Ich will dies in gebotener Kürze tun. Wem es jetzt zu mühsam ist, dem Gedankengang zu folgen, der kann die folgenden eingerückten Absätze vorerst überschlagen; er muss die Formel halt einfach so hinnehmen.

Wenn man gedanklich sämtliche N Taxis der Stadt nach aufsteigenden Nummern hintereinander anordnet und dann die beobachteten Taxis markiert, dann liegt es nahe, davon auszugehen, dass die Abstände zwischen den markierten Taxis alle in derselben Weise verteilt sind und folglich auch denselben Mittelwert haben. Aber es gibt die Schwierigkeit mit Anfang und Ende der Liste: Wie viele Taxis mit Nummern kleiner als a gibt es und wie viele oberhalb des Maximalwerts b?

Um diese Schwierigkeit zu umgehen, greifen wir zu demselben Trick wie beim Das-erste-Ass-Problem. Allerdings müssen wir unser Gedankenmodell entsprechend vorbereiten. Sicherlich ist es für die Statistik egal, ob man sich im Café die Nummern merkt, oder ob man die vorbei kommenden Taxis irgendwie markiert, indem man beispielsweise einen Zettel auf die Rückbank legt – rein gedanklich. Die Taxis brauchen dazu gar nicht nummeriert zu sein. Wir können – ohne die Statistik wesentlich zu stören – diese Nummerierung sogar nachholen. Wir stellen uns nun vor, dass sämtliche Taxis zum Nummerieren auf einen riesigen Betriebshof gebracht werden. Um mit der Nummerierung irgendwo anfangen zu können, fügen wir ein weiteres Taxi hinzu und geben ihm die Nummer 0.

Nun ordnen wir sämtliche Taxis rein zufällig im Kreis an. Das entspricht dem Mischen eines Spielkartenstapels. Das Zusatztaxi mit der Nummer 0 spielt hier die Rolle eines zufällig gesetzten Ortes, an dem die fortlaufenden Nummerierung beginnt, so wie wir beim Kartenstapel eine Karte eingefügt haben, die den Ort markierte, wo der Stapel beim Abheben geteilt wird. Vom 0-Taxi ausgehend folgen wir dem Kreis, beispielsweise im Uhrzeigersinn, und vergeben fortlaufend die Nummern 1, 2, 3, …, N.

Um zu zeigen, dass die Einfügung eines 0-Taxis an den statistischen Verhältnissen nichts ändert, muss man sich nur klar  machen, dass jede zyklische Anordnung der Taxis einschließlich 0-Taxi eine Eins-zu-eins-Entsprechung in der linearen Anordnung der Taxis hat — letztere ohne das Zusatztaxi.

Die Nummern der beobachteten und markierten Taxis erscheinen nun in aufsteigender Folge. Weil alle Taxis unterschiedslos behandelt worden sind, können wir davon ausgehen, dass die Abstände zwischen aufeinanderfolgenden Markierungen derselben Statistik genügen. Der Mittelwert der insgesamt n+1 Abstände zwischen den Taxis einschließlich des 0-Taxis lässt sich folglich durch den Quotienten (N+1)/(n+1) errechnen. Wenn wir nun – ausgehend vom 0-Taxi – nur die folgenden n Abstände betrachten, den Abstand des b-ten Taxis zum darauf folgenden 0-Taxi also außer Acht lassen, erhalten wir mit b/n eine weitere Abschätzung dieses mittleren Abstands. Gleichsetzen dieser beiden Mittelwerte und Auflösen nach N liefert die gesuchte Formel für den Schätzwert.

Die Formel b*(n+1)/n-1 bezeichnen wir als erste Schätzung. Sie scheint ein wenig windig zu sein: Nur der Maximalwert b kommt darin davor. Wir nutzen nur ein Minimum der verfügbaren Information. Deshalb besorgen wir uns eine weitere Schätzung über eine Symmetriebedingung: Es werden im Mittel genauso viele Zahlen unterhalb des Minimalwerts a liegen, nämlich a-1, wie oberhalb des Maximalwerts b, nämlich N–b. Gleichsetzung ergibt die zweite Schätzung für N, nämlich a+b-1 = 1021.

Die zweite Schätzung nutzt schon mehr Information als die erste, nämlich a und b. Wäre es nicht noch besser, alle Taxinummern für die Schätzung heranzuziehen? Wir können beispielsweise den Mittelwert m aller beobachteten Nummern berechnen und diesen mit dem Mittelwert (N+1)/2 der Zahlen von 1 bis N gleichsetzen. So erhalten wir die dritte Schätzung: 2m – 1 = 945. Ein Mangel dieser Schätzung fällt sofort ins Auge: Der Schätzwert für N kann kleiner als b werden, im Widerspruch zu den Tatsachen.

Nun wollen wir noch wissen, was es mit diesen Schätzungen auf sich hat und wie gut sie sind. Dazu realisiere ich eine kleine Simulation mit dem PC. Der Rechner führt viele Male hintereinander das folgende Experiment durch: Erzeugung von 20 paarweise verschiedenen Zufallszahlen aus dem Bereich von 1 bis 1000. Jede Zahl hat dieselbe Chance, ausgewählt zu werden. Jedes Mal werden die Schätzwerte nach den drei Formeln berechnet.

Schließlich werden die Mittelwerte der Schätzungen über sämtliche Versuche sowie deren Standardabweichung (ein Maß für die Streuung) ermittelt. Es zeigt sich, dass alle Schätzer erwartungstreu sind: Für jeden Schätzer ergibt sich ein Mittelwert (Erwartungswert) von 1000, was ja genau die für den Test angenommene Anzahl von Taxis ist. Für den ersten Schätzer ist die Standardabweichung gleich 48, für den zweiten gleich 66 und für den dritten gleich 129.

Fazit. Je mehr Information in die Schätzungen einfließt, desto schlechter wird sie. Hier gilt also nicht „Viel hilft viel“, sondern „Weniger ist mehr“.

Aber Hoppla! Das kann nicht durchweg stimmen. Es kommt darauf an, auf welche Information man sich stützt und welche man ignoriert. Und für diese Entscheidung sind dann doch wieder Rationalität und umfassende Kenntnis der Problemlage gefragt. In diesem Sinne hilft viel dann tatsächlich viel. Wie man mit der Weniger-ist-mehr-Heuristik daneben liegen kann, zeigt uns eine vierte Schätzung auf der Basis der kleinsten beobachteten Nummer: a*(n+1)-1 = 1427. Auch diese Schätzung ist erwartungstreu. Von daher lässt sich nichts gegen die Formel sagen. Aber die Streuung der Schätzwerte ist exorbitant. Die Standardabweichung ist gleich 944. Die Schätzung taugt nichts.

Die folgende Tabelle zeigt die Ergebnisse des Simulationsexperiments für die ersten 20 Versuche für alle vier der von mir vorgestellten Schätzformeln.

Die Schätzergebnisse aus den ersten 20 Versuchen der stochastischen Simulation

Weiterlesen →

Veröffentlicht unter Bildungswesen, Heuristik, Schule und Hochschule, Statistik, Tests, Wahrscheinlichkeitsrechnung | Verschlagwortet mit , , , , | Ein Kommentar

Je ne suis pas Charlie

Veröffentlicht am 18. Januar 2015 von Timm Grams

Es gibt Anlass zur Trauer. Viele gehen auf die Straße. Am 11. Januar 2015 in Paris sind es eineinhalb Millionen Menschen. Unsere Verachtung gegenüber der Killertruppe von Paris besteht zu Recht. Und ja: Satire wie die von Charlie Hebdo muss möglich sein.

Das Bekenntnis „Je suis Charlie“ trifft auf unser Mitgefühl. Der Bundespräsident meint gar, dass wir alle Charlie seien. Wir bekennen uns zur Satire dieser Zeitung, so wie sich Kennedy am 26. Juni 1963  zum bedrohten Berlin bekannte, als er sagte: „Ich bin ein Berliner“.

Aber Hoppla! So aufgewühlt wir auch sind, sollten wir nicht vergessen, über Zweck und Wirkung der Demonstrationen nachzudenken. Damals im Kalten Krieg waren Beistand und Identifikation gefragt. Heute geht es vor allem um Trauer und es ist nicht ausgemacht, dass unsere Trauer erst durch die Identifikation mit der religionskritischen Satirezeitschrift echt ist.

Als Schüler und Student habe ich gern die Pardon (später: Titanic) gelesen. Satire hat mir Spaß gemacht, Religionskritik inbegriffen. Heute frage ich mich eher, was sie bezweckt und erreicht. Meine Freude daran hat nachgelassen.

Also: Ich bin nicht Charlie.

Möglicherweise geraten wir in unserer Trauer genau in die Falle, die uns die Killertruppe von Paris stellt: Wir übernehmen deren falsches Begründungsmuster, nämlich dass diese Schandtaten aus dem rechten Glauben folgen.

Gegen einen Machtapparat wie den IS, der die Religion als Begründung seines weltlichen Macht- und Alleinvertretungsanspruchs ganz im archaischen Sinne gebraucht, hilft Satire von außen nicht. Spott wird die Islamisten nicht zur Umkehr bringen. Eher werden der Binnenzusammenhalt als auch der Hass gegen Anders- und Nichtgläubige größer.

Wir müssen fragen, wie die Jugendlichen zu Fanatikern und religiös motivierten Killern werden. Dann kommen wir schnell auf die sozialen Ursachen und auf das Bildungswesen. Auch in Deutschland hängt der Schulerfolg noch viel zu stark von der sozialen Herkunft ab. Hier liegen die wahren Baustellen unserer Gesellschaft: Bessere Bedingungen für Zuwanderer. Chancengleichheit in der Bildung. Dafür lohnt es sich, zu demonstrieren.

Eine andere Frage ist, welche Rolle die Religion in unserer Gesellschaft spielt und spielen soll. In dieser Frage stehen Grundrechte miteinander im Konflikt: Auf der einen Seite die Glaubens- und Bekenntnisfreiheit und auf der andern die Meinungs- und  Pressefreiheit (Art. 4 und 5 GG). Der Paragraf 166 StGB über die Beschimpfung von Bekenntnissen und Religionsgemeinschaften ist Ausdruck der Balance, die unsere Gesellschaft in dieser Frage gefunden hat. Das ist immer wieder neu zu verhandeln. Manchen geht der Schutz der Religionen nicht weit genug, anderen geht er zu weit. Religionskritische Zeitschriften wie Charlie Hebdo beziehen eindeutig Stellung. Das ist gut so; aber nicht jeder muss ihre Haltung teilen.

Dass unsere Trauer so eng mit Religionskritik verbunden wird, lässt nichts Gutes erwarten. Erst der halbwegs kühle Kopf befähigt uns, das Richtige tun.

Veröffentlicht unter Bildungswesen, Schule und Hochschule, Skeptizismus, Soziologie, Spiritualität | Verschlagwortet mit , , , | Ein Kommentar

iPad-Klassen: Evaluation 2.0

Veröffentlicht am 31. Dezember 2014 von Timm Grams

Den Jubelmeldungen über die neu eingeführten iPad-Klassen an Schulen bin ich seinerzeit mit Misstrauen begegnet. Insbesondere die fehlende Kontrolle des Lernerfolgs erweckte meinen Argwohn (iPad-Klassen: unkontrollierte Experimente an jungen Menschen).

Für mich gehören der Computer und dessen Einsatz in Lehrveranstaltungen zum beruflichen Alltag. Es geht hier also nicht um eine pauschale Verurteilung von neuen Medien im Unterricht. Will man etwas über den pädagogischen Nutzen des Computers im Unterricht erfahren, muss man verschiedene Aspekte beleuchten. Das betrifft wenigstens die folgenden Felder:

  1. Technische Hilfsmittel: Lese-, Schreib-, Kommunikationswerkzeuge im ansonsten weitgehend traditionellen Unterricht, Herausbildung von Computer- und Medienkompetenz. Computergestütztes Arbeiten: Analyse-, Simulations- und Konstruktionswerkzeuge.
  2. Arbeitsverhalten: Individualisierung des Lernens, mobiles Lernen, neue Kommunikationsformen, Wandel im Miteinander und im Unterrichtsstil.
  3. Computergestütztes Lernen: eLearning, Edutainment
  4. Gefahren: Suchtverhalten.

Über ein Jahr nach dem ersten Bericht über das „Leuchtturm-Projekt“ liegt nun ein weiterer vor: „iPad-Klassen-Projekt wird weiter ausgebaut“ (Fuldaer Zeitung, 23.12.2014, S. 15) und „Großer Schritt in Richtung Schule 2.0“ (Osthessen News, 11.12.2014).

Als Erfolg wird hervorgehoben, dass der „Webauftritt der iPad-Klasse“ im  „Google-Ranking […] eine Top-Platzierung erzielt“ habe. Das nenne ich Evaluation 2.0. Ein Logo und eine „Corporate Identity“ habe man inzwischen auch. Es ist, als gälte es Brühwürstchen zu verkaufen. Der Bildungsauftrag gerät zur Nebensache. Viel besser kann man meine vor Jahren geäußerten Befürchtungen eigentlich nicht illustrieren: „Oberflächenkompetenz und Konsumverhalten. Trends im Bildungswesen – eine kritische Betrachtung“ (THEMA Hochschule Fulda 2/2006, S. 4-6).

Die bereits vor über einem Jahr angekündigte seriöse Begleitstudie zum iPad-Klassen-Projekt hat wohl noch keine Ergebnisse erbracht. Jedenfalls ist davon nichts zu vernehmen. Ich verbleibe in gespannter Erwartung.

Bei sorgfältig erwogenem Einsatz sind mit dem Computer sicherlich gute Lernerfolge zu erzielen. Zur Debatte stehen vor allem die Punkte Hilfsmittel und Arbeitsverhalten. Aber zweifellos kann man auch einiges falsch machen. Hinsichtlich des Computeruntstützten Lernens (eLearning und Edutainment) ist die allgemeine Ernüchterung heute bereits ziemlich groß und zum Suchtverhalten gibt es schon seit Jahren Warnungen von berufenen Leuten.

Hier interessiert besonders die Frage, inwieweit das Lernen von Mathematik durch den frühen Einsatz von computergestützten Werkzeugen in der Schule gefördert oder gar behindert wird. Ich denke da an Dynamische-Geometrie-Software (DGS) und an Computer-Algebra-Systeme (CAS).

Dass es sich um ein brennend aktuelles Problem handelt, wird mir ständig vor Augen geführt: Viele meiner Studenten gehen mathematische Herausforderungen eher lustlos an. Ich empfinde sie als trostlose Gestalten, denen offenbar nie das Glücksgefühl zuteil wurde, das sich mit der selbst vollbrachten Lösung eines schweren mathematischen Problems einstellt. Möglicherweise wurde ihnen die Freude an der Mathematik auch durch den Computer verdorben. Was ich damit meine, habe ich in der Ministudie Erfolgserlebnisse beim Lernen und deren Verhinderung mittels Computer zum Ausdruck gebracht.

Ähnliche Erfahrungen und Erkenntnisse liegen in der Mathematikdidaktik vor. Das in der Fachwelt verfügbare Wissen geht weit über meine eher anekdotische Beweisführung hinaus. Aufschlussreich ist der Aufsatz „Zum Einfluss der Informatik auf die Mathematikdidaktik. Weiterhin nur Computereinsatz und noch immer keine Medienbildung?“ von Horst Hischer.

Die Begleitstudie zum iPad-Klassen-Projekt sollte sich dieses Themas annehmen. Es hat auch mit der Zukunftsfähigkeit unserer Gesellschaft zu tun.

Veröffentlicht unter Bildungswesen, Schule und Hochschule, Tests | Verschlagwortet mit | 3 Kommentare

Argumentationsfehler des ontologischen Naturalismus

Veröffentlicht am 3. September 2014 von Timm Grams

Unfug

„Darf man Unfug Unfug nennen?“ heißt es in der Ankündigung eines Vortrags, in dem es um die Abgrenzung zwischen Wissenschaft und Pseudowissenschaft gehen soll. Unterstellungen, nämlich dass die Naturwissenschaftler sich eine solche Abgrenzung zu einfach vorstellten und dass der von ihnen vorgebrachte „populäre Verweis auf Falsifizierbarkeit recht wenig zur Abgrenzung“ tauge, sollen auf den Vortrag neugierig machen. Es wird ein Rezept versprochen, „wie man dennoch sinnvoll Fug von Unfug voneinander unterscheiden kann“.

In dem Vortrag wird es wohl um den ontologischen Naturalismus gehen. Er ist der gedankliche Hintergrund, vor dem sich approximativ wahre Erkenntnis von Illusion (Mahner, 2007) und damit „Fug von Unfug“ scheiden lassen. Nach dieser Maßgabe sind dann „Bereiche wie Astrologie, Kreationismus oder Homöopathie“ leicht als Unfug erkennbar.

Hier will ich – in skeptischer Grundhaltung – die Argumente, die für den ontologischen Naturalismus vorgebracht werden, in Zweifel ziehen. Aber Achtung: Der Umkehrschluss, dass damit die genannten Bereiche der Parawissenschaften vom Verdikt des Unfugs freigesprochen würden, ist keinesfalls erlaubt. Auch findet sich im Folgenden kein Plädoyer für irgendeine vermeintlich bessere Weltanschauung. Dieser Artikel soll und wird niemanden von seinem Glauben abbringen. Der Naturalist soll seine Ontologie aber auch nicht als Denknotwendigkeit „verkaufen“ können. Ein solcher Geltungsanspruch steht in fundamentalem Widerspruch zum Skeptizismus.

Die Argumente

Den Kern des ontologischen Naturalismus bildet die Keine-Übernatur-Hypothese: Die Welt ist kausal geschlossen und es gibt keine Wechselwirkung mit so etwas wie einer Übernatur.

Dabei wird durchaus zugestanden, dass Hypothesen dieser Art – anders als wissenschaftlichen Aussagen – grundsätzlich „nicht empirisch prüfbar“ sind (Mahner, 2007). Da sie dem Falsifizierbarkeitskriterium für wissenschaftliche Aussagen folglich nicht genügen, haben sie den Rang von metaphysischen Hypothesen. Das heißt aber, dass es sich beim ontologischen Naturalismus um ein Glaubenssystem handelt.

Diese Einstufung des Naturalismus will vielen seiner Vertreter nicht so recht gefallen. Als Ausweg wird angesehen, dass diese Hypothesen wenigstens kritisierbar seien. Falls sich der Diskussionspartner auf dieses Wischiwaschi nicht einlässt, wird gelegentlich behauptet, dass die „Keine-Übernatur-Hypothese“ doch grundsätzlich widerlegbar sei.

Obwohl dieses Argument nicht von allen Verteidigern des ontologischen Naturalismus ins Feld geführt wird, nehme ich es in die folgende Sammlung von Argumenten auf, um im Zuge der Widerlegung dieses Arguments dem Hin und Her zu begegnen: Die „Keine-Übernatur-Hypothese“ ist tatsächlich NICHT falsifzierbar, sie ist metaphysisch.

Es folgen einige der zentralen Argumente des ontologischen Naturalismus. Im folgenden Kapitel widme ich mich den Mängeln dieser Argumente.

  1. „Der ontologische Naturalismus [ist] eine notwendige Voraussetzung der Realwissenschaften.“ (Mahner, 2007) Er ist eine unverzichtbare Bedingung dafür, dass keine merkwürdigen Dinge passieren, dass es sozusagen in der Welt mit rechten Dingen zugeht. Die Prüfung wissenschaftlicher Theorien ist nur in einem naturalistischen Kontext möglich. Durch die Möglichkeit supranaturaler Manipulation verlieren Beobachtung, Messung und Experimente den Status als empirische wissenschaftliche Methoden. „Überprüfbar ist […] nur etwas, mit dem wir wenigstens indirekt interagieren können und das sich gesetzmäßig verhält. Übernatürliche Wesenheiten entziehen sich hingegen per definitionem unserem Zugriff und sind auch nicht an (zumindest weltliche) Gesetzmäßigkeiten gebunden.“ (Mahner, 2007)
  2. „Die Wissenschaften [wurden] immer erfolgreicher […], je konsequenter sie die geistesgeschichtlich bedingten supranaturalistischen Überreste aus ihrem Weltbild entfernt haben.“ (Mahner, 2009)
  3. Die Keine-Übernatur-Hypothese ist falsifizierbar. „Der Naturalismus könnte scheitern, indem wir die Welt plötzlich so vorfänden, wie sie im zeitgenössischen Kino- und Fernseh-Gruselgenre gezeichnet wird, wo Vampire, Dämonen, Teufel und Erzengel aus und ein gehen und Dinge tun, die man nur als Wunder betrachten kann.“ (Mahner, 2007).
  4. Nullhypothese. Der ontologische Naturalismus ist die Nullhypothese der Naturwissenschaften. (Mahner, 2007; Neukamm, 2009)
  5. Erkennbarkeit. Die reale Welt existiert und sie kann auch erkannt werden. „Naturgesetze sind Eigenschaften von Dingen“ (Mahner, 2001).
  6. Die Alternative zur Annahme einer Erkennbarkeit der Welt ist eine konsequent relativistische Position. Wissenschaft ist dann nur noch ein Diskurs wie jeder andere ohne Anspruch, die Realität wenigstens näherungsweise zutreffender zu beschreiben und zu erklären als andere Bereiche. (Dieses Argument wurde in einer privaten Kommunikation mit dem Hinweis auf das Bullshit-Buch von Harry Frankfurt garniert. S. d. Artikel Kontrastbetonung. S. a. Körkel, 2014)
  7. Insbesondere das entsprechend den aktuellen wissenschaftlichen Erkenntnissen geeignet modifizierte Kausalitätsprinzip („Alles hat eine Ursache“) haftet der Natur an. Es ist Wesensmerkmal der „Dinge an sich“. „Nach der These des ontologischen Naturalismus ist der Kosmos kausal strukturiert und in sich abgeschlossen.“ (Neukamm, 2009)
  8. Approximationspostulat. „[Man muss] in einer realistischen Wissenschaftsphilosophie davon ausgehen, dass wissenschaftliche Gesetzesaussagen mehr oder weniger gute (d.h. approximative) Repräsentationen objektiver Gesetze in der Natur sind.“ (Mahner, 2001)

Fehleranalyse und Widerlegungen

In den Diskussionen mit Naturalisten begegnet einem immer wieder eine Argumentationsfigur: Das Dilemma-Argument. Beim Dilemma wird für eine Position Zustimmung dadurch erheischt, dass man dieser Position eine unhaltbare Alternativposition (einen Strohmann sozusagen) gegenüberstellt und diese dann widerlegt. Auf dieses Argumentationsmuster fällt herein, wer sich auf die damit verbundene Blickverengung einlässt und übersieht, dass es außer der aufgezeigten auch noch andere und nicht so leicht zu erledigende Alternativen gibt.

Ich nehme mir jetzt jedes der oben aufgeführten Argumente vor und zeige das jeweilige Argumentationsmuster und dessen fehlleitende Wirkung auf.

  1. Hier wird die Glaubensneigung des Menschen ausgenutzt (DENKFALLEN UND PARADOXA). Wer einfach glaubt, was er liest, entlastet seinen Denkapparat. Dem Sparsamkeitsprinzip folgend, schalten wir für gewöhnlich erst dann in den anspruchsvollen Denkmodus, wenn es unplausibel wird. Genau das wollen wir jetzt einmal tun. Dass es in der Welt nach unseren Erfahrungen mit rechten Dingen zugeht, ist unter anderem mit der Annahme verträglich, dass Gott die Welt geschaffen und sie dann weitgehend sich selbst überlassen hat. Viele andere Beispiele für jenseitige Eingriffsmöglichkeiten bei gleichzeitiger Ermöglichung von Wissenschaft findet der Interessierte im Kino, beispielsweise im Film Matrix der Wachowski-Geschwister, und in der Bibel. Sogar gelegentliche Wunder würden die Wissenschaft nicht im Herz treffen. Der Glaube an Gott und seine wunderbare Schöpfung scheint mir sogar eine stärkere Triebkraft der Wissenschaft zu sein als die Annahme irgendeiner abstrakten Ontologie. Bezeichnend ist ja, dass die Zeit höchster religiöser Erregung im Gefolge der Reformation und der Religionskriege mit der Blütezeit der modernen Wissenschaft zusammenfällt: Galilei, Descartes und Pascal beispielsweise waren zutiefst religiöse Menschen. Dasselbe gilt für Kopernikus, Kepler und Newton (Larson/Witham: Naturwissenschaftler und Religion in Amerika. Spektr. d. Wiss. 11/1999, S. 74-78). Kurz: Der ontologische Naturalismus ist keineswegs „notwendige Voraussetzung der Realwissenschaften“. Wissenschaft gedeiht offensichtlich im Kontext ganz unterschiedlicher Begründungssysteme. Ich halte es für gleichgültig, woher der Forscher seine Motivation bezieht, denn: Die Hauptsache ist der Effekt.
  2. Beim Argument, „dass die Wissenschaften immer erfolgreicher wurden, je konsequenter sie die geistesgeschichtlich bedingten supranaturalistischen Überreste aus ihrem Weltbild entfernt haben“, werden Korrelation und Kausalität miteinander verwechselt (DENKFALLEN UND PARADOXA). Nehmen wir einmal an, die negative Korrelation zwischen Wissenschaft und Glauben besteht tatsächlich; dann liegt die Vermutung nahe, dass der Glaube aufgrund der zunehmenden wissenschaftlichen Erkenntnis schwindet und nicht etwa umgekehrt. Vielleicht aber haben beide Effekte auch eine gemeinsame Ursache. Als Kandidat kommt der gesellschaftliche Wandel infrage, der natürlich selbst wieder von den genannten Einflussgrößen und anderen abhängt. Also: So einfach, wie im zweiten Argument dargestellt, ist die Sache sicher nicht. Und wenn der Glaube an die Übernatur schwindet, heißt das noch lange nicht, dass anstelle dieses Glaubens ein anderer, nämlich der an den ontologischen Naturalismus treten muss. Die Welt der Zweifler am Supranaturalen scheint mir ziemlich bunt zu sein. Und einigen, insbesondere manchem Agnostiker, sind philosophische Überlegungen dieser Art fremd, denn: Ein gelingendes (Forscher-)Leben ist auch ohne Ontologie möglich.
  3. Dass die Keine-Übernatur-Hypothese falsifizierbar sei, ist ein ganz gewöhnlicher Fehlschluss. Die Beobachtung einer die Hypothese widerlegenden „übernatürlichen“ Erscheinung wie beispielsweise die Gedankenübertragung würde diese sofort zu einem Phänomen der realen Welt machen. Das Phänomen würde also nicht mehr der falsifizierenden Übernatur zugerechnet. Die falsifizierende Übernatur bliebe, falls es sie tatsächlich gäbe, der Erkenntnis unerreichbar. Daraus folgt, dass die Keine-Übernatur-Hypothese – nicht anders als die Annahme eines Schöpfergottes –  unwiderlegbar und somit eine Glaubensangelegenheit ist.
  4. „Nullhypothese“ ist in diesem Zusammenhang ein Täuschwort. Der Manipulant vertraut darauf, dass dieser Begriff einen gewissen Sog in Richtung des Natürlichen, in Richtung dessen, was keinerlei Begründung mehr bedarf, entwickelt. Der Begriff ist der schließenden Statistik entlehnt; dort hat man es – anderes als hier – mit messbaren und prüfbaren Dingen zu tun. Der Begriff täuscht Seriosität vor.
  5. Die Annahme der Erkennbarkeit der Welt steht im Widerspruch zur alten und vielbe­stätigten Erkenntnis, dass wir keinen unmittelbaren Zugriff auf die Realität haben; was wir erkennen können, sind die Erscheinungen der Dinge und nie die „Dinge an sich“. Je mehr die Physik der Welt zu Leibe rückt, desto mehr scheint die Realität zurückzuweichen. Was übrig bleibt, sind Formeln. Meinhard Kuhlmann schreibt: „Die Theorie sagt uns zwar, was wir messen können, aber sie spricht in Rätseln, wenn es um die Frage geht, was eigentlich hinter unseren Beobachtungen steckt“ und weiter „Physikalische Theorien können empirisch gültig sein, ohne metaphysische – jenseits der Physik liegende – Fragen zu klären“ („Was ist real?“,  Spektrum der Wissenschaft, Juli 2014, S. 52).
  6. Es handelt sich um ein klassisches Dilemma-Argument: Es wird so getan, als gäbe es nur Erkenntnis der Realität und Wahrheit einerseits und alternativ dazu einen bedeutungsarmen Diskurs und Pseudowissenschaft. Das ist auch eine Art Strohmann-Argument. Die Alternative kommt so abschreckend daher, dass man sie ablehnen muss. Selbstverständlich gibt es weitere Alternativen, und darunter sind weit plausiblere als die hier präsentierte. Meine Lieblingsalternative ist der kritische Rationalismus des Karl Raimund Popper. Er kommt ohne Weltanschauung aus. Aber niemand muss deswegen auf seine Weltanschauung verzichten. Der kritische Rationalismus ist so etwas wie der größte gemeinsame Teiler unter den Wissenschaftlern. Selbst Popper bekennt sich darüber hinaus zum Realismus; aber er betont, dass seine Logik der Forschung den Realismus nicht voraussetzt (Drittes Intermezzo: Was ist Pseudowissenschaft?).
  7. Die Kausalitätserwartung, also die Erwartung, dass es zu jedem Geschehnis eine Ursache gibt, ist ein angeborener Lehrmeister (Konrad Lorenz). Das Kausaldenken ist Grundlage der empirischen Wissenschaften und des freien Willens. Unsere Handlungen erfahren wir als Ursache dessen, was sich daraufhin entwickelt. Dasjenige, was von der getroffenen Entscheidung abhängt, ist die Wirkung. (Der Billardspieler sieht den Stoß, also die Krafteinwirkung, als Ursache der Kugelbewegung. Wer im Kettenkarussell sitzt, der verspürt die Fliehkraft als Wirkung, verursacht durch die Kreisbewegung seines Sitzes.) Ursache-Wirkungs­beziehungen sind der Hebel, mit dem es uns gelingt, den Lauf der Welt in unserem Sinne zu beeinflussen. Das Kausalitätsprinzip („Alles hat eine Ursache“) wurde im Laufe der Zeit immer wieder neu interpretiert, je nach Fortgang der Wissenschaft. Kurz: Das Kausalitätsprinzip wird gelernt. Es ist unserem Erkenntnisapparat zuzuordnen und nicht einer für uns letztlich unerkennbaren „objektiven Realität“.
  8. Approximations- bzw. Näherungsverfahren dienen dazu, „Lösungen mathematischer Probleme in endlich vielen Schritten mit definierter Genauigkeit“ anzunähern (Brockhaus). Für die Genauigkeit der Annäherung an die Realität liefert die Wissenschaft – anders als es das Wort „approximativ“ unterstellt – keine Anhaltspunkte. Dass Repräsentationen objektiver Gesetze approximativ seien, ist so gesehen eine irreführende Formulierung. Karl Raimund Popper und Hans Albert haben realistischere Vorstellungen. Ich habe sie durch mein Stöckchen-Beispiel im Artikel Kontrastbetonung veranschaulicht.

Die hier aufgespießten Argumentationsmuster wie das Dilemma, der Strohmann und das Täuschwort schöpfen das Repertoire der Kämpfer für den ontologischen Naturalismus bei weitem nicht aus. Neben allgemeinen Fehlschlüssen und Fehldeutungen wird genommen, was die Trickkiste der fehlleitenden Argumentation so hergibt. (Ich gebe hier nur wieder, was ich in Diskussionen erlebt habe.) Ein einfacher und aus der Werbung gut bekannter Trick ist die Holzhammermethode: Widerlegte Behauptungen werden einfach ständig wiederholt. Und dann gibt es noch den Stellvertreter: Wenn du nicht beweisen kannst, was du beweisen willst, dann demonstriere etwas anderes und behaupte, es sei dasselbe (Ein X für ein U). Beispielsweise habe ich von einem Verteidiger des ontologischen Naturalismus diesen Satz gelesen: „Ob die Welt im strengen Sinn kausal geschlossen ist, weiß niemand.“ Da muss eine ganz andere Weltanschauung, ein Stellvertreter, dahinter stehen, denn: Die kausale Geschlossenheit der Welt ist das fundamentale Postulat des ontologischen Naturalismus und eigentlich nicht verhandelbar. Viele Beispiele für Stellvertreter- und Strohmann-Argumente findet der interessierte Leser im Artikel von Körkel: Immunisierungsstrategien stehen dort stellvertretend für das illusionäre Denken, Wahrnehmungsberichte über die Realität treten anstelle der Erkennbarkeit der Welt; für meinen Standpunkt muss der radikale Skeptizismus als Strohmann herhalten, wahlweise auch Kants transzendentales Verfahren, der subjektive Wahrheitsbegriff oder der radikale Konstruktivismus, usw. (Diesen Absatz habe ich am 4.10.2014 nachgetragen.)

Fazit und Ausblick

Es scheint ziemlich egal zu sein, ob ein Wissenschaftler seine Motivation aus dem Glauben an einen Gott, aus dem Glauben an einen ontologischen Naturalismus oder allein aus dem Erfolg der Wissenschaft bezieht. In den Labors und auf Fachtagungen spielen die verschiedenen Begründungssysteme folglich auch kaum eine Rolle; sie treten im Forschungsalltag nicht groß in Erscheinung. Die Verständigung gelingt allein auf der Basis der Logik der Forschung. Durch den Verzicht auf Missionierung und jeglichen Beglückungsanspruch wird das Leben leichter und jeder kann sich dem widmen, was auch dem Skeptiker am Herzen liegt – die Wissenschaft.

Quellen

Martin Mahner: Naturgesetz – naturphilosophische Aspekte. Naturwissenschaftlichen Rundschau 54(9), 2001, 505-506

Martin Mahner: Unverzichtbarkeit und Reichweite des ontologischen Naturalismus. In: Zufall Mensch, 2007 (Hrsg. Lars Klinnert), S.77-90

Martin Mahner: Demarcating Science from Non-Science. Handbook of the Philosophy of Science – Focal Issues, pp. 515-575, Elsevier 2007

Martin Mahner: Religion und Wissenschaft. Materialien und Informationen zur Zeit, 03.09.2009

Martin Neukamm: Der ontologische Naturalismus ist keine Ideologie, sondern die Nullhypothese der Naturwissenschaften. Aufklärung und Kritik 1/2009, S. 94-109

Manfred Feodor Körkel: Sind Naturalismus und Skeptizismus kompatibel? Blog-Artikel 2014

Veröffentlicht unter Logik, Naturwissenschaften, Skeptizismus, Wissenschaft und Pseudowissenschaft | Verschlagwortet mit , , , , , , , , , , | 15 Kommentare

Kontrastbetonung

Veröffentlicht am 27. Juni 2014 von Timm Grams

Wirst du aber […] alles tun, was ich dir sage, so will ich deiner Feinde
Feind und deiner Widersacher Widersacher sein. Ja, mein Engel wird vor dir
hergehen und dich bringen zu den Amoritern, Hethitern, Perisitern,
Kanaanitern, Hewitern und Jebusitern, und ich will sie vertilgen.

2. Mose 23, 22-23

Hüte dich, einen Bund zu schließen mit den Bewohnern des Landes,
in das du kommst, damit sie dir nicht zum Fallstrick werden in deiner Mitte;
sondern ihre Altäre sollst du umstürzen und ihre Steinmale zerbrechen
und ihre heiligen Pfähle umhauen; denn du sollst keinen andern Gott anbeten.
Denn der HERR heißt ein Eiferer; ein eifernder Gott ist er.

2. Mose 34, 12-14

„Bullshit? Bingo!“ überschreibt ein „Skeptiker“ seinen Blog-Artikel. Bullshit ist ein in „Skeptiker“-Kreisen gern genommener Kraftausdruck, mit dem die Abscheu gegenüber Äußerungen von Homöopathen und paranormal „Begabten“ zum Ausdruck gebracht wird. Um auch ja nicht falsch verstanden zu werden, beruft man sich auf das Heftchen Bullshit des US-amerikanischen Philosophen Harry Gordon Frankfurt.

Bullshit

Ich kann diesen 42-seitigen und prätentiös in Buchform gebrachten Text – der Titel „Bullshit“ der Suhrkamp-Taschenbuchausgabe ist in erhabenen(!) Buchstaben gesetzt – nicht ernst nehmen. Für mich handelt es sich um eine Faschingsvorlesung, um einen Vortrag also, den Professoren halten, wenn sie die Gepflogenheiten ihres Faches einmal durch den Kakao ziehen wollen. Mit professoraler Akribie und unter ausufernder Diskussion von Quellenmaterial, nicht zu vergessen das Oxford English Dictionary, verbreiten sie sich dann über ein lächerliches Thema. Was in diesem Fall dabei herauskommt, ist genau das, was der Titel verspricht: breitgetretener Bullshit. Spaßig.

Textprobe: „Es scheint durchaus angebracht, zwischen achtlos hergestellten, minderwertigen Produkten und Bullshit eine Parallele zu sehen. Aber in welcher Hinsicht? Liegt die Übereinstimmung darin, dass auch Bullshit stets achtlos und ohne jede Sorgfalt produziert wird, dass er nie fein gearbeitet ist, dass sich bei seiner Herstellung niemals die penible Aufmerksamkeit fürs Detail findet, von der Longfellow spricht? Ist der Bullshitter seinem Wesen nach ein geistloser Banause? Ist sein Produkt in jedem Fall grob und unsauber gearbeitet? Das Wort shit verweist natürlich darauf. Exkremente sind niemals in besonderer Weise gestaltet und gearbeitet. Sie werden nur ausgeschieden und entsorgt. Sie mögen eine mehr oder weniger in sich geschlossene Form haben, aber ganz sicher sind sie nicht ‚mit größter Sorgfalt gearbeitet‘.“

Mancher „Skeptiker“ nimmt den Bullshit-Text offenbar ernst. Er empfindet ihn als Rückenwind für seine Angriffe gegen Para- und Pseudowissenschaftler. Die „Bullshit“-Metapher dient ihm der Kontrastbetonung. Sie gibt seinen verbalen Attacken die rechte Würze. In der “Skeptiker”-Ecke des Internets gibt es denn auch eine Bullshit Police, ein Bullshit-Blog, eine Bullshit-Olympiade und diverse Bullshit-Bingos.

Freund oder Feind?

Eine kleine Textprobe: „Ich möchte mit meinen Zuschauern meinen Bullshitdetektor schärfen und begebe mich dafür in die vernunftverlassensten Ecken der Esoterik, Verschwörungstheorien und Pseudowissenschaften, ziehe Bullshitter aus ihren Löchern und lege jede ihrer Aussagen auf die Goldene Waage der Wahrheit.”

Da kommt ein ziemlich einfaches Weltbild zum Vorschein: Der „Skeptiker“ versucht Wahrheit und Bullshit zu trennen; er selbst steht auf der Seite der Wahrheit, seine vermeintlichen oder tatsächlichen Gegenspieler hingegen reden Bullshit.

Was derartiges bipolar ausgerichtetes Denken anrichten kann, zeigt der ehemalige U.S.-Präsidenten George W. Bush. Er gibt sich als überzeugter Christ, als Born-Again. Dem Journalisten Bob Woodward gegenüber erklärte er seinerzeit, dass er auf Ratschläge seiner Berater und auf Unterstützung durch seinen Vater, den früheren Präsidenten, verzichten könne, da er „einen höheren Vater“ konsultiere (The Faith Factor. TIME, 21.6.2004, S. 36-41). Damals ging es um den Einmarsch in den Irak.

George W. Bush steht auf der Seite des Guten, denn Gott ist mit ihm. Seine Gegner bilden die Achse des Bösen. Die TIME vom 30 Juni 2014 präsentiert – ganz aktuell – auf der Titelseite das katastrophale Ergebnis dieses bipolaren Denkens: THE END OF IRAQ.

Der Vergleich ist ziemlich drastisch, ja übertrieben; das gebe ich zu. Und den „Skeptikern“ wird er gar nicht gefallen. Er zeigt nämlich die Nähe ihrer Argumentation zu derjenigen ihrer Gegner. Aber genau darum geht es mir: um die Grundmuster der Argumentation, die auf beiden Seiten anzutreffen sind.

Ontologie für Rechthaber

Die Argumentationsweisen, die ich hier meine, zeichnen sich alle durch einen unangreifbaren Dreh- und Angelpunkt aus. Gott ist ein solcher. Wer ihn auf seiner Seite hat, ist im Recht und im Besitz der Wahrheit. Und wie sieht er bei den „Skeptikern“ aus?

Da sich die „Skeptiker“ als Anwälte der Wissenschaften verstehen, müsste man meinen, dass ihre Argumentationskultur streng an wissenschaftlichen Grundsätzen orientiert ist. Aber damit haben sie ein Problem, denn: Wissenschaft kann keine absoluten Wahrheiten bieten. In den empirischen Wissenschaften ist das Weltbild von den Wahrheitsbesitzern einerseits und den Bullshittern andererseits nicht unterzubringen.

Für den Bekehrungseifer hin zur Wahrheit lässt sich dem Felde der Wissenschaft also kein Schwung abgewinnen. Der  „Skeptiker“ braucht aber die sichere Basis. Er muss sich des Besitzes der Wahrheit, nämlich der (unwandelbaren) Naturgesetze, gewiss sein können. Erst dann kann er das Gefühl haben, dass seine Angriffe und Hohn- und Spottaktionen gerechtfertigt sind.

Harry Frankfurt zeigt einen Rettungsweg zum Heil – ob ernst gemeint oder nicht. Er drückt seine Botschaft so aus: „Wer […] nicht mehr an die Möglichkeit glaubt, bestimmte Aussagen als wahr, andere hingegen als falsch auszuweisen, dem bleiben nur zwei Wege. Entweder er stellt jegliche Versuche ein, die Wahrheit zu sagen bzw. zu lügen. Das bedeutet, auf Tatsachenbehauptungen ganz und gar zu verzichten. Oder er stellt weiterhin Behauptungen auf, die den Anspruch auf eine Beschreibung der Wirklichkeit erheben, aber nichts anderes als Bullshit sein können.“

Und weiter: „Die gegenwärtige Verbreitung von Bullshit hat ihre tieferen Ursachen auch in diversen Formen eines Skeptizismus, der uns die Möglichkeit eines zuverlässigen Zugangs zur objektiven Realität abspricht und behauptet, wir könnten letztlich gar nicht erkennen, wie die Dinge wirklich sind. Diese ‚antirealistischen‘ Doktrinen untergraben unser Vertrauen in den Wert unvoreingenommener Bemühungen um die Klärung der Frage, was wahr und was falsch ist, und sogar unser Vertrauen in das Konzept einer objektiven Forschung. Eine Reaktion auf  diesen Vertrauensverlust besteht in der Abkehr von jener Form der Disziplin, die für die Verfolgung eines Ideals der Richtigkeit erforderlich ist, und in der Hinwendung zu einer Disziplin, wie sie die Verfolgung eines alternativen Ideals erfordert, nämlich eines Ideals der Aufrichtigkeit.“

Da der „Skeptiker“, seinem Selbstbild entsprechend, sicherlich keinen Bullshit redet, weiß er sich, Harry Frankfurt im Umkehrschluss folgend, im Besitz eines „zuverlässigen Zugangs zur objektiven Realität“, wie auch immer dieser aussehen mag. Der „Skeptiker“ hat den Blick für das Wesen der Dinge, er ist im Besitze einer Ontologie. Die damit einhergehenden metaphysischen Hypothesen haben den Vorteil, prinzipiell nicht widerlegbar zu  sein. Das schafft Sicherheit, ist Gott-Ersatz.

Kurz oder lang?

Harry Frankfurt hat sicherlich nur Spaß gemacht, denn „objektive Forschung“ steht keineswegs infrage, nur weil wir „gar nicht erkennen, wie die Dinge wirklich sind“. Nach Karl Raimund Popper liegt „die Objektivität wissenschaftlicher Sätze […] darin, dass sie intersubjektiv nachprüfbar sein müssen“ (Logik der Forschung, 8. Abschnitt). Ein unmittelbarer Zugriff auf die Realität ist für unseren Erkenntnisapparat leider unmöglich, für eine objektive Wissenschaft aber glücklicherweise auch verzichtbar. Objektivität lässt sich rein diesseitig erreichen.

Harry Frankfurt meint (vermutlich im Spaß), man könne über Wahrheit in der Wissenschaft im Positiv reden („was wahr ist und was falsch ist“). Das sehen die  Erkenntnistheoretiker Karl Raimund Popper, Hans Albert und Gerhard Vollmer anders. Sie reden über mehr oder weniger Wahrheitsnähe, also konsequent im Komparativ. Anstelle von Frankfurts „zuverlässigem Zugang zur objektiven Realität“ sehen sie nur eine mehr oder weniger gute Annäherung an die Realität. In Bildern gesprochen: Wenn ich zwei Stöckchen vorgelegt bekomme, kann ich sehr wohl sagen, welches länger ist und welches kürzer. Ob das längere lang oder das kürzere kurz ist, kann ich nicht entscheiden, solange mir ein absoluter Maßstab fehlt.

Auch das Reden im Superlativ ist durchaus in Ordnung, zum Beispiel ist folgende Rede möglich: Unter den bekannten Theorien r, s, t, u, … ist die Theorie r diejenige, die der Wahrheit am nächsten kommt, eben weil sie wenigstens die von den Theorien s, t, u, … erklärten empirischen Sachverhalte ebenfalls erklärt und weil sie umfassender, präziser oder besser geprüft ist als jene.

Von einem Vertrauensverlust in das Konzept einer objektiven Forschung kann also nicht die Rede sein, nur weil wir „letztlich gar nicht erkennen, wie die Dinge wirklich sind“. Allerdings bekommt der Begriff der objektiven Erkenntnis eine Bedeutung, die ihm durch Karl Raimund Popper beigemessen wird; er steht nicht für die Erkenntnis einer objektiven Realität.

Übrigens: Können Sie sich einen Moralphilosophen vorstellen, der Aufrichtigkeit für Bullshit hält, bloß weil er meint, der Mensch könne eben auch nicht die Wahrheit über sich selbst erkennen?

Veröffentlicht unter Logik, Naturwissenschaften, Skeptizismus, Wissenschaft und Pseudowissenschaft | Verschlagwortet mit | Schreib einen Kommentar

„Skeptiker“ kontra Skeptiker über Kreativität in der Wissenschaft

Veröffentlicht am 11. Juni 2014 von Timm Grams

Die Welt der Skeptiker ist bunt. Das ist gut so. Skeptiker erheben das Zweifeln zum Prinzip. Und natürlich zweifelt der Skeptiker auch an den verschiedenen Spielarten des Skeptizismus. Da bleiben Kontroversen nicht aus. Es kann sich lohnen, eine solche Kontroverse einmal genauer zu beäugen. Daraus lässt sich etwas über das skeptische Argumentieren lernen.

Im Artikel „Der mörderische russische Yeti vom Djatlow-Pass“, verfasst vom „Skeptiker-Chefreporter“, stieß mir dieses mit Wohlwollen weitergereichte Zitat auf:

Ein Dauerthema in der Bullshitistic ist der „brillante Ketzer“. Gläubige sind oft der Überzeugung, die Wissenschaft werde von verkannten Außenseitern vorangebracht, deren fabelhafte Theorien zunächst abgelehnt, später jedoch als der neueste Stand der Erkenntnis anerkannt werden. Nichts könnte falscher sein. Umwälzende Innovationen entstehen nicht auf der Grundlage eigenbrötlerischer Träumereien. Sie sind vielmehr die Folge massiver gemeinsamer Forschungsanstrengungen und des gegenseitigen Datenaustausches […]

In diesen Zeilen wird für mich die in Skeptiker-Kreisen weit verbreitete Blindheit gegenüber dem Wesen schöpferischer Prozesse deutlich. Mein Kommentar: „Hier offenbart der Schreiber eine verblüffende und sicherlich von ihm unbemerkte Nähe zur Anthroposophie. Beispielsweise meint Prof. Dr. Olaf-Axel Burow, der diesen Kreisen ebenfalls nahesteht: ‚Kreativität gibt es nur im Plural‘. Seine Rezepte auf Grundlage des von ihm zum phantastischen ‚kreativen Feld‘ überhöhten Zusammenschlusses von ‚Persönlichkeiten mit stark unterschiedlich ausgeprägten Fähigkeiten, die eine gemeinsam geteilte Vision verbindet‘, bringen möglicherweise technische Optimierungsvorgänge wie die von ihm angesprochenen Entwicklungen des Rolls-Royce, des Apple-Computers und des Mountain-Bikes voran; die wirklich umstürzenden Erfindungen wie die des Buchdrucks, des Telefons, des Computers, des WWW, des Penicillins kommen so aber nicht zustande. Was bei der Lehre vom kreativen Feld herauskommt, ist eine Sammlung von Trivialtäten, wie ‚die Weisheit der Vielen‘ und all das, was man die Tugenden des Mittelmaßes nennen könnte: Teamfähigkeit, Flexibilität, ‚Fokus auf die Zukunft‘. Genau auf diesem Niveau hält sich der Blog-Artikel auf.“

Ich weise im Kommentar auf meine Abschiedsvorlesung hin, in der ich die gegenteilige Auffassung vertrete: Es ist nicht das Team, das erfindet, und neue Lösungen werden auch keinesfalls zielgerichtet angegangen. Der Geistesblitz ereignet sich stets in einem einzigen Kopf! Meist entdecken die Genies rein zufällig Lösungen für Probleme, die sie eigentlich gar nicht hatten.

Mein Diskussionsbeitrag zum Skeptiker-Artikel endet so: „Und noch etwas, das für die Skeptiker mit oberflächlichem Wissenschaftsverständnis ziemlich schwer verdaulich sein dürfte: In den Kaptiteln 2, 6, 7 und 8 seiner Aufsatzsammlung ‚Vermutungen und Widerlegungen‘ bringt Karl Raimund Popper – sicher kein Schwärmer für das Okkulte – eine Reihe von Beispielen aus der Wissenschaftsgeschichte, die die Bedeutung des mystischen und metaphysischen Denkens für das Entstehen neuer Theorien zeigen. Unter anderem: Die Zahlenmystik des Pythagoras ist Quelle das Atomismus; die newtonsche Mechanik ist aus Mythen entstanden; die religiös-neuplatonische Idee, dass der Sonne der höchste Platz im Universum gebührt, war Ausgangspunkt der kopernikanischen Wende.“

Nicht einmal eine halbe Stunde später kommt die Replik des „Skeptiker-Chefreporters“ auf meinen Kommentar. Er bezieht sich zunächst auf meine Bemerkung zur Rolle von Zahlenmystik, Mythen und religiös-neuplatonischen Ideen und schreibt:

Mit dem kleinen Unterschied, dass Newton eben nicht bei den Mythen stehengeblieben ist und diese immer weiter vertieft hat, bis er sich völlig im Mythologischen verloren hat, ebenso wenig wie Kopernikus mit „Ideen“ hausieren ging, sondern sich ein Fernrohr genommen und seine Vermutungen überprüft und schließlich bewiesen hat.

Ja, natürlich, in den Parawissenschaften wird die kritische Seite der empirischen Wissenschaft – nämlich das Deduzieren und Prüfen – sträflich vernachlässigt. Mir wird fälschlich unterstellt, diese Seite übersehen zu haben. Nur: Es ist halt die kreative Seite der Wissenschaft, auf die ich das Augenmerk lenken wollte; deshalb bleibt die kritische Seite unerwähnt. Das Unerwähnte eignet sich prächtig für ein Strohmann-Argument, wie wir gesehen haben. Im Artikel geht es gerade so weiter:

Alles, was er [der „Yeti-Explorer“] herausgefunden hat, weist genau in die gegenteilige Richtung eines „Yeti-Monsters“.

Damit wird mir die Absicht untergeschoben, die Yeti-Monster-Geschichte zu verteidigen. Auch das ist ein Argumentationsfehler. Der Zweifel an einem Argument für eine bestimmte Auffassung zieht nämlich noch lange nicht die Auffassung selbst in Zweifel. Der „Skeptiker-Chefreporter“ macht etwas, das dem Scheitern am Modus Tollens gleich kommt: Aus der Aussage, „Wenn es regnet, gehe ich ins Kino“ lässt sich eben nicht schließen, dass ich auf das Kino verzichte, wenn es nicht regnet.

Das Strohmann-Argument wird weiter ausgewalzt, und zwar in der Replik auf meine Bemerkung „Meist entdecken die Genies rein zufällig Lösungen für Probleme, die sie eigentlich gar nicht hatten“:

Pseudowissenschaftler entdecken eben nicht zufällig „Lösungen“ für echte Probleme noch beschäftigen sie sich überhaupt mit „echten“ Problemen der Wissenschaft, sondern sie sind von diversen Phantastereien überzeugt, ohne dafür jemals Belege zu liefern, und die die „echte“ Wissenschaft längst abgehakt hat.

Als hätte ich das angezweifelt. Der „Skeptiker-Chefreporter“ beantwortet schließlich meine Bemerkung, dass in Skeptiker-Kreisen die Blindheit gegenüber dem Wesen schöpferischer Prozesse weit verbreitet sei, mit dieser Köstlichkeit:

Gewiss ja – erzählen Sie das bitte jemandem, der keine 25 Bücher geschrieben hat, aber nicht mir.

Der „Skeptiker“ sollte eigentlich wissen, dass der Vorwurf der Majestätsbeleidigung – und darum handelt es sich hier ja – dem Skeptiker einem inneren Vorbeimarsch gleichkommt. Wer jetzt noch nicht genug hat, der kann ja den gesamten  Blog-Artikel des „Skeptiker-Chefreporters“ samt Kommentaren lesen.

Wo kann man etwas über den Skeptizismus lernen? Im Buch über „Antike und moderne Skepsis“ von Markus Gabriel (Junius Verlag, 2008). Und wo findet man eine gute Zusammenstellung von Argumentationsfiguren – manchmal irreführend, manchmal auch nützlich? In „Wie man mit Fundamentalisten diskutiert, ohne den Verstand zu verlieren“ von Hubert Schleichert (Beck, 1997).

Veröffentlicht unter Heuristik, Logik, Naturwissenschaften, Skeptizismus, Wissenschaft und Pseudowissenschaft | Verschlagwortet mit , , , | Schreib einen Kommentar

GWUP: Esoterik durch die Hintertür

Veröffentlicht am 3. Mai 2014 von Timm Grams

Die Vereinigung der Kausalität als Freiheit mit ihr als Naturmechanismus,
davon die erste durchs Sittengesetz, die zweite durchs Naturgesetz,
und zwar in einem und demselben Subjekte, dem Menschen, fest steht,
ist es unmöglich, ohne diesen in Beziehung auf das erstere als
Wesen an sich selbst, auf das zweite aber als Erscheinung,
jenes im reinen, dieses im empirischen Bewusstsein vorzustellen.
Ohne dieses ist der Widerspruch der Vernunft mit sich selbst unvermeidlich.

Immanuel Kant
Aus der Vorrede zur Kritik der praktischen Vernunft, 1788

Warum der GWUP beitreten?

Die Gesellschaft zur wissenschaftlichen Untersuchung der Parawissenschaften (GWUP) hat sich der Entlarvung vorgeblich paranormal Begabter verschrieben; mit besonderer Inbrunst widmen sich einige Mitglieder des Vereins der Verhöhnung von Anhängern alternativer, insbesondere homöopathischer Heilverfahren. Zur Zielgruppe der GWUP gehören Leute, die nicht immer und überall dem Credo der Wissenschaft oberste Geltung einräumen wollen – was vielen GWUPlern scheinbar gründlich missfällt.

Es fragt sich, ob das publizistische Getöse der relativen Harmlosigkeit der Zielgruppe angemessen ist: Der Markt der allopathischen Mittel ist etwa hundertmal größer als derjenige der homöopathischen. Wenn man dazu bedenkt, dass die homöopathischen Mittel keine Wirkung entfalten (außer dem Placeboeffekt vielleicht) und daher wohl auch keine schädliche, dann muss man die Risiken der Allopathie um mehrere Größenordnungen höher einschätzen als jene der Homöopathie.

Ja, es gibt auch die redlich um Aufklärung und Fairness besorgten Skeptiker. Sie finden es beispielsweise schwer erträglich, dass die pseudowissenschaftliche Homöopathie staatliche Förderung genießt. Die  wachsende Präsenz von Pseudowissenschaften an Hochschulen aufgrund von Drittmitteln und Stiftungsprofessuren ist für sie besorgniserregend. Und sie möchten, im Sinne der Verbraucheraufklärung, sachliche Informationen zu außerordentlichen Vorgängen und Geltungsansprüchen bieten. Für diese Skeptiker ist die GWUP eine Heimstatt.

Trotz mancher offensichtlichen Übertreibungen gibt es gute Gründe, dem Verein beizutreten. Ich fand diese in der Selbstdarstellung des Vereins: „Wir sind Frauen und Männer mit unterschiedlichen Biografien, Berufen und Fachrichtungen: Wissenschaftler, Journalisten, wissenschaftlich Interessierte. In unseren Weltanschauungen sind wir sehr verschieden. Uns verbindet jedoch die Überzeugung, dass Wissenschaft und kritisches Denken für die gesellschaftlichen Herausforderungen von heute und morgen wichtiger sind denn je. Wir nennen uns Skeptiker. Das heißt, wir betrachten ungewöhnliche Behauptungen zwar mit Skepsis, lehnen sie aber nicht vorschnell ab, sondern prüfen sie mit wissenschaftlichen Methoden und den Instrumenten des kritischen Denkens.“

Schon lange interessiert mich die Frage, was wir Menschen überhaupt wissen können. In der GWUP wird augenscheinlich um Antworten gerungen. Mit Beginn des Jahres 2006 wurde ich Vereinsmitglied.

Was stutzig macht

Aber Hoppla! Es kam zu Ereignissen, die mich an der Aufrichtigkeit der Selbst­darstellung der GWUP zweifeln ließen. Der erste Kontakt mit dem Hausphilosophen der GWUP – eine Art Torwächter – verlief, wenn ich mich recht erinnere, so:

– Sie sind Herr Grams, neu hier.

– Ja.

Dann kam die Gretchenfrage. Meine Antwort: Ich bin Agnostiker.

– Aha, weichgespülter Atheist.

– Nein, überzeugter Agnostiker.

Der missbilligende Gesichtsausdruck ließ in mir den Verdacht aufkeimen, hier fehl am Platze zu sein. Am Büchertisch zeigte und empfahl mir der Torwächter sein neuestes Werk; das war ein unmissverständlicher Hinweis darauf, wie man hier zu ticken hat. Allein der stramme Atheist ist gern gesehen. Weltanschauliche Toleranz sieht anders aus.

Auf einer der ersten Jahreshauptversammlungen, die ich besuchte, gab es den Antrag, in die Satzung die Möglichkeit der Vereinsmitgliedschaft von Kindern aufzunehmen. Mutig wagte ich meine erste Wortmeldung: Führen wir dann auch die Kommunion ein? Glücklicherweise war der vom Vorstand unterstützte Antrag dann erst einmal vom Tisch. Ein seltsames Gebaren zeigte sich da: Vehement gegen Weltanschauungen kämpfen und dann flugs die eigene in die entstehende Lücke stopfen.

In der Zeitschrift skeptiker und auch auf den Jahrestagungen kommen immer wieder dieselben Leute zu Wort. Die Veranstaltungen haben den Charakter der Selbstvergewisserung. Die Bestätigungssucht und das Ausschließen von Selbstzweifeln gehören aber sicherlich nicht zu den Skeptikertugenden. Sie sind charakteristisch für das hermetische Denken, wie es so typisch für die Esoterik ist.

Solche Beobachtungen haben mich irritiert. Aber erst mit der Zeit schwante mir, dass da mehr dahinter steckt, nämlich ein System.

Ein Irrglaube macht sich breit

Als ich mich für meinen Hoppla!-Artikel Was ist Pseudowissenschaft? auf die GWUP-Definitionen der Begriffe Parawissenschaft und Pseudowissenschaft berufen wollte, stellte ich fest, dass die offizielle Begriffsbestimmung in der GWUP-Information zum Thema Parawissenschaft – Pseudowissenschaft nicht mit derjenigen übereinstimmt, die ich aus der Satzung kenne.

In der Satzung wird die Abgrenzung zwischen Wissenschaft, Para- und Pseudowissenschaft so definiert: „Unter Pseudowissenschaften werden Aussagesysteme verstanden, die Anspruch auf Wissenschaftlichkeit erheben, ohne ihn einzulösen; unter Parawissenschaften solche, bei denen Zweifel besteht, ob sie diesem Anspruch genügen.“

Die GWUP-Information zum Thema „Parawissenschaft – Pseudowissenschaft“ hingegen gibt eine Neudefinition: „Eine Parawissenschaft […] ist ein außerhalb der Wissenschaften […] angesiedelter Erkenntnisbereich, dessen Theorie und Praxis weitgehend auf illusionärem Denken beruhen […] ‚Parawissenschaft‘ ist daher eine neuere, an die Bezeichnung ‚Parapsychologie‘ angelehnte Wortbildung, die es erlaubt, den Begriff ‚Pseudowissenschaft‘ auf seine engere Bedeutung zu beschränken.“

In dieselbe Richtung geht die Präambel der Vereinszeitung: „Aus einer interdisziplinären Perspektive hinterfragt [der Skeptiker] den Wahrheitsgehalt von parawissenschaftlichen Behauptungen kritisch, undogmatisch und mit wissenschaftlichen Methoden.“

Beim flüchtigen Lesen werden die harten Konsequenzen dieser Definitionen und ihr Widerspruch zur Satzung nicht ins Auge fallen. Aber hoppla: Wenn es heißt, dass „Wahrheitsgehalt“ hinterfragt werde, dann unterstellt man, dass wir so etwas wie die Wahrheit erkennen können, und dass die Hüterin dieser Wahrheit die GWUP bzw. deren Vereinsorgan ist.

Offenbar steht die Neudefinition auf einer weltanschaulichen Grundlage, einer Ontologie, die über das Wesen der Dinge Auskunft gibt. Wenn man genauer hinsieht, findet man den ontologischen Naturalismus, der auf den Philosophen Mario Bunge zurückgeht.

Mario Bunge suchte nach den Prinzipien der Realität. Letztere sind für ihn und seine Adepten Martin Mahner und Gerhard Vollmer zumindest partiell erkennbar; sie erhalten den Rang von Postulaten, Forderungen also, die sachlich notwendig, wenn auch nicht beweisbar sind. Unter anderem will Martin Mahner das Kausalitätsprinzip als der Realität anhaftend ausgemacht haben.

Und wer solche ewigen Wahrheiten erst einmal erkannt hat, der kann sich auch ein Urteil darüber erlauben, inwieweit andere dieser Wahrheit nahe kommen, inwieweit ihr Denken wahre Erkenntnis liefert oder ob es illusionär ist.

Diese Attitüde ist unbegründet – eine unverstellte Anmaßung. Und von dieser Anmaßung ist die Satzung der GWUP frei. Ihr Anliegen ist unabhängig von Weltanschauungen formuliert und hat allein Wissenschaftsbezug. Das ist der von mir gemeinte Widerspruch zwischen offiziellen Verlautbarungen und Satzungstext.

„Es sind uns Dinge als außer uns befindliche Gegenstände unserer Sinne gegeben, allein von dem, was sie an sich selbst sein mögen, wissen wir nichts, sondern kennen nur ihre Erscheinungen.“ Spätestens seit Immanuel Kant diese starken Worte geäußert hat, müssen wir einsehen, dass der ontologische Naturalismus niemals die erhofften Antworten liefern kann. Mario Bunges Suche nach den Prinzipien der Realität war von Anfang an zum Scheitern verurteilt.

Dabei hat ein Vertreter des ontologischen Naturalismus vor vielen Jahren selber klar gemacht, was von den Postulaten dieser Philosophie zu halten ist. In seinem Büchlein „Evolutionäre Erkenntnistheorie“ aus dem Jahre 1983 hat Gerhard Vollmer uns die kantschen Aprioris, sie entsprechen den Postulaten, mittels Evolutionstheorie sehr schön erklärt. Sie seien stammesgeschichtlich erworbene Anpassungen: phylogenetisch a posteriori und ontogenetisch a priori. Derartige Anpassungen erweisen sich durch ihren Überlebenswert. Sie haften nicht einer objektiven und von uns erkennbaren Realität an; sie sind unserem Erkenntnisapparat zuzurechnen. Konrad Lorenz spricht in diesem Zusammenhang von angeborenen Lehrmeistern. Und diese angeborenen Lehrmeister sind keineswegs ewig gültig und richtig; manchmal müssen wir ihnen sogar widerstehen, wie das System der Denkfallen zeigt.

Bereits Immanuel Kant lokalisierte die Möglichkeiten des Erkennens in der Vernunft und nicht etwa in den Offenbarungen einer absoluten Realität. Er unterschied sogar zwei Arten der Vernunft. Einmal kann Erkenntnis gewonnen werden durch Spekulation und Erfahrung unter Anleitung der Aprioris. So funktioniert es in den Naturwissenschaften.

Andererseits muss man ohne Empirie auskommen und hat als Prüfstein für die Spekulation nur das Handeln. So liegen die Verhältnisse in Sachen Freiheit und Moral. Diese beiden Denkweisen wurden von Kant in verschiedenen Büchern abgehandelt, nämlich zum einen in seiner „Kritik der reinen Vernunft“ und zum anderen in der „Kritik der praktischen Vernunft“.

Amardeo Sarma, der Vereinsvorsitzende, hält „eine GWUP-Arbeit ohne die Annahme zumindest eines ontologischen Realismus für nicht möglich“ und schreibt: „Dabei wäre ich vermutlich sogar mit vielen Theologen einig. Streit hätte ich mit ihnen ‚nur‘ bezüglich der Zahl der angenommenen realen Entitäten. Sich nur auf einen intersubjektiven Konsens zu berufen halte ich für abwegig.“

Dass die Theologen das so sehen müssen, ist wohl klar. Für sie existiert ja auch Gott. Aber sie geben auch nicht vor, empirische Wissenschaft zu treiben; deshalb werden sie nicht in Argumentationsnöte geraten. Aber wenn wir Skeptiker uns auf diese Schiene setzen lassen, kommen wir in dieselben Begründungsnöte wie die Kreationisten oder Intelligent-Design-Leute mit ihrem Wissenschaftsanspruch.

Mit dem Ausspruch, dass „Prüfbarkeit […] die Existenz des zu Prüfenden voraus[setzt]  und nicht nur, dass wir uns aufgrund von Prüfungen (von was denn eigentlich?) einigen“ steht Sarma außerhalb der heute weithin akzeptierten Epistemologie. Natürlich prüft der Wissenschaftler nicht die „Existenz des zu Prüfenden“, sondern er prüft Theorien, also Aussagen über Zusammenhänge zwischen Erscheinungen. Ich glaube, dass – außer Theologen, Esoterikern und ontologischen Naturalisten vielleicht – kein ernstzunehmender Forscher die Existenz einer Energie beispielsweise nachweisen will.

Parawissenschaft (Satzung kontra Neudefinition)

Parawissenschaft (Satzung kontra Neudefinition)

Die grafische Gegenüberstellung der Definition laut GWUP-Satzung und der Neudefinition des Begriffs der Parawissenschaft führt uns vor Augen: Die GWUP-Satzung ist bescheiden und lässt Glaubenssysteme und Religionen außen vor. Sie beschränkt sich allein auf den Aspekt der Wissenschaftlichkeit von Erkenntnissystemen, insoweit sie einen solchen Anspruch vertreten.

Die Neudefinition des Begriffs der Parawissenschaft weitet das Zielgebiet der GWUP drastisch aus, und zwar auf alles, was nicht der wahren Erkenntnis dient. Mahner geht dann so weit und sagt, dass „schließlich auch Religionen … unter den Begriff Parawissenschaften“ fallen. Meine Kritik an Mahners Vorschlag habe ich seinerzeit mit Viel Feind, viel Ehr? überschrieben.

Da der ontologische Naturalismus wegen seiner unbeweisbaren Postulate selbst ein Glaubenssystem ist, manövriert er, insoweit er Grundlage der Arbeit sein soll, die GWUP in eine aussichtslose Lage: Sie beruft sich auf ein Glaubenssystem, um Glaubenssysteme ausgrenzen zu können. Das ist paradox.

Zirkelschlüsse und Selbstwidersprüche zuhauf

Der ontologische Naturalismus ist unhaltbar. Zirkelschlüsse und Selbstwidersprüche sind unvermeidlich. Eine dieser Zwickmühlen konnten wir schon im letzten Abschnitt besichtigen, hier folgen ein paar weitere.

Selbstimmunisierung

Der ontologische Naturalismus nimmt in den Denkvoraussetzungen, den Postulaten, das an, was er eigentlich erst zeigen will. Gerhard Vollmer spricht beschönigend von einem Circulus Virtuosus, einem Wunderzirkel sozusagen. Meine Traumsatire macht die Widersprüchlichkeit dieses Ansatzes deutlich.

Selbstwiderspruch

Wenn Martin Mahner und Gerhard Vollmer von einer zumindest partiell erkennbaren Realität sprechen und den Wahrheitsbegriff benutzen, der die Nähe unseres Wissens zu dieser Realität angibt, dann können diese Postulate gar nicht Hypothesen im wissenschaftlichen Sinn sein: Die Postulate bilden ja die Messlatte der Wahrheitsnähe von Theorien. Sie selbst zum Gegenstand der Widerlegungsversuche zu machen, läuft auf einen unlösbaren Selbstwiderspruch hinaus.

Dieser dem ontologischen Realismus innewohnende Selbstwiderspruch wurde von Gerhard Roth in einem Streitgespräch mit Gerhard Vollmer deutlich gemacht: „Entweder man ist Realist und sagt, die Welt ist zumindest partiell erkennbar, oder man sagt, alles ist hypothetisch, dann ist man Konstruktivist.“ (In „Wahrheit und Wirklichkeit – Wirklichkeit und Wahrheit“, Protokolle der Evangelischen Akademie Braunschweig, 4./5. Juni 1993, erschienen 1994)

Roth lehnt den Realismus im Sinne von Vollmer, Mahner und Bunge jedenfalls ab, und zwar aus rein logischen Gründen, zwingend also.

Und was ist mit der Freiheit?

Nach dem ontologischen Naturalismus gibt es eine Realität, die wenigstens teilweise erkennbar ist. Zu den Gesetzmäßigkeiten dieser Realität gehört das Kausalitätsprinzip („Alles was geschieht hat eine Ursache“). Nun ist der Mensch selbst Bestandteil dieser Realität und gemäß dem ontologischen Naturalismus kausal bestimmt. Wie steht es dann mit der Freiheit? Kausalitätsprinzip und Entscheidungsfreiheit lassen sich nicht miteinander vereinbaren. Lässt sich die Idee der Freiheit aufgrund dieser einfachen Argumentation eliminieren? Wohl nicht.

Das Kausalitätsprinzip muss angepasst werden. Auch die Quantenphysik legt eine Abänderung nahe. Unausweichliche Konsequenz ist, dass das „Prinzip“ dem Wissensfortschritt folgt und nicht starr sein kann. Es ist plastisch. Demzufolge kann es gar nicht der objektiven Realität anhaften, sondern es ist unserem Erkenntnisapparat zuzuordnen. Das „Prinzip“ wird gelernt!

Hier wäre Gelegenheit, sich mit dem Kant-Zitat eingangs dieses Artikels zu beschäftigen: Kant entgeht dem fatalen Zirkel, indem er Kausalität und Freiheit verschiedenen Betrachtungsweisen zuordnet: dem empirischen Bewusstsein einerseits und dem reinen praktischen Bewusstsein andererseits. (Lassen Sie sich von Kants gewundener Schreibe nicht abschrecken: Die Gedanken sind von außerordentlicher Klarheit.)

Die Rettung: Rückbesinnung

Anders als die Neudefinition der Begriffe Para- und Pseudowissenschaft sind die Definitionen der GWUP-Satzung weltanschaulich neutral. Es geht nur um epistemologische Fragen und nicht um Fragen nach dem Wesen der Dinge (Onotolgie). Und dabei sollte es bleiben. Übrigens gibt auch Gerhard Vollmer, obwohl bekennender Realist, in seiner jüngsten Schrift „Gretchenfragen an den Naturalisten“ die satzungsgemäße Definition der Begriffe an.

Der ontologische Naturalismus wird – wie jede andere Ontologie auch – für die GWUP-Arbeit nicht gebraucht. Er führt sie weg von ihrem Kerngeschäft.

Die satzungsgemäße Begriffsbestimmung ist klar und leistungsfähig und sie lässt Spielraum für differenzierende Analysen. Die Neudefinition hingegen basiert auf einem Glaubenssystem, das die Asymmetrie von Behauptung und Widerlegung ersetzt durch die Symmetrie von Behauptung und Gegenbehauptung. Letzteres führt zu fruchtlosen zirkelhaften Debatten. Lassen wir die Finger davon!

Veröffentlicht unter Biologie, Logik, Naturwissenschaften, Physik, Skeptizismus, Wissenschaft und Pseudowissenschaft | Verschlagwortet mit , , , , | 26 Kommentare

GWUP: Wohin des Wegs?

Veröffentlicht am 17. Februar 2014 von Timm Grams

Einst hatt ich einen bösen Traum

Till: Ein Freund, von dem ich Jahrzehnte nichts gehört hatte, ging mir vor ein paar Tagen im Kopf herum. Und – du wirst es nicht glauben – kurz darauf meldet er sich per Telefon. Obwohl ich da etwas skeptisch bin: Das war Gedankenübertragung! Oder was sagst du dazu? Du bist doch unser Oberskeptiker und sogar Mitglied in einem Verein gleichgesinnter Leute.

Manni: Das mit der Gedankenübertragung hast du dir eingebildet. Es war reiner Zufall. Denn: Gedankenübertragung ist etwas Paranormales, eine pure Illusion. Mit der Realität hat das nichts zu tun.

Till: Woher willst du das wissen?

Manni: In unserem Verein, in der Gesellschaft zur wissenschaftlichen Untersuchung von Parawissenschaften, haben wir Philosophen. Sie geben uns mit ihrer Philosophie eine wichtige Grundlage für unsere Entlarvungsaktionen in Sachen Astrologie, Homöopathie, Paranormales und anderen Humbugs.

Till: Ihr habt also eine Philosophie. Wie sieht die denn aus?

Manni: Ich sage es einmal ganz einfach. Wir setzen voraus, dass es eine Realität außerhalb unseres Bewusstseins gibt, die bestimmten Gesetzmäßigkeiten folgt. Überall in dieser Welt geht es mit rechten Dingen zu. Insbesondere postulieren wir, dass mentale Kräfte niemals kausal wirksam werden können. Wir nennen es das Kein-Psi-Prinzip. Diese Philosphie hat auch einen Namen. Es ist der hypothetische ontologische Realismus oder Naturalismus. Er ist die Denkbasis unserer Aktionen und Publikationen.

Till: Au wia, ziemlich kompliziert das alles. Aber was hat das mit meiner Frage zu tun?

Manni: Nach unseren Denkvoraussetzungen gibt es keine geistartigen Kräfte und Wirkungen, kein Psi; und ohne den Faktor Psi gibt es auch keine Gedankenübertragung. Und das wolltest du doch wissen.

Till: Versteh ich dich richtig? Ihr setzt voraus, dass es kein Psi gibt und daraus folgert ihr, dass es kein Psi geben kann und dass deshalb Gedankenübertragung unmöglich ist? Das sieht mir sehr nach einem Zirkelschluss oder Teufelskreis aus: Ihr Skeptiker geht von der Voraussetzung aus, dass es in der Welt mit rechten Dingen zugeht und dann folgert ihr daraus, dass es in der Welt mit rechten Dingen zugeht, ein formidabler circulus vitiosus.

Circulus virtuosus

Manni: Ja, es handelt sich um einen Selbstbezug; das hast du richtig bemerkt. Aber der ist nicht gefährlich. Anders als beim Lügnerparadoxon kommt es hier nicht zu einem Widerspruch. Und eine Abwärtsspirale droht auch nicht. Der ontologisch-hypothetische Selbstbezug ist sogar äußerst fruchtbar und erlaubt uns Skeptikern, einen stabilen Standpunkt einzunehmen. Er ist unangreifbar, sozusagen immun gegen jedes Gegenargument. Wir nennen ihn folglich auch nicht Teufelskreis oder Circulus vitiosus. Das wäre altes Denken. Für uns, die Vertreter des neuen Denkens, ist es ein Circulus virtuosus, ein virtuoser, ein Wunderzirkel sozusagen.

Till: Tja, wenn da so ist…

Ich wache auf. Das Herz klopft. Ich versuche meine Gedanken zu ordnen. Voller Unruhe gehe ich hinüber in meine kleine Bibliothek. Es folgt ein hastiges Stöbern in den Ordnern und Büchern. Da ist nichts zu lesen von einem hypothetischen ontologischen Realismus. Auch das Stichwort Circulus virtuosus ist unauffindbar.

Erschöpft und erleichtert

Was ich finde, ist all das mir Vertraute. In der GWUP-Satzung lese ich die bescheidenen aber gehaltvollen Sätze: „Unter Pseudowissenschaften werden Aussagesysteme verstanden, die Anspruch auf Wissenschaftlichkeit erheben, ohne ihn einzulösen; unter Parawissenschaften solche, bei denen Zweifel besteht, ob sie diesem Anspruch genügen.“

Nur auf Wissenschaft wird Bezug genommen. Was Wissenschaft ist, wissen die Wissenschaftler ziemlich genau, egal ob sie ontologische Naturalisten, Realisten, Christen, Agnostiker und was sonst noch sind. Und nach den Spielregeln der Wissenschaft lässt sich sicherlich auch klären, was an der Gedankenübertragung dran ist.

Aber das ist ja schon geschehen, und zwar in der US-Army in den Fünfzigerjahren und dann noch einmal in den Achtzigerjahren – mit niederschmetterndem Misserfolg. Heute lachen wir über die Bestrebungen, das Paranormale militärisch zu nutzen. Es gibt ein Buch über diese Abenteuer: „The men who stare at goats“. Es wurde mit George Clooney, Ewan McGregor, Jeff Bridges und Kevin Spacey verfilmt. Köstlich!

Aufgeräumt und erleichtert gehe ich zu Bett und sinke in einen erholsamen Schlaf.

Veröffentlicht unter Logik, Spiritualität, Wissenschaft und Pseudowissenschaft | Verschlagwortet mit , , | Ein Kommentar