Abgrenzung
In diesem Weblogbuch taucht immer wieder die Frage auf, wann eine Erkenntnis als wissenschaftlich einzustufen ist und wo die Grenzen zur Pseudowissenschaft liegen. Hier will ich meine Annäherung an einen Standpunkt zu dieser Frage offen legen.H
Als Leitfaden für eine Einordnung der Wissenschaften soll die folgende Tabelle dienen. Erkenntnissysteme, die nicht den Anspruch der Wissenschaftlichkeit haben, liegen außerhalb dieser Betrachtung. Insbesondere sind das die schönen Künste (Malerei, Musik, Belletristik) und die Religionen. Die Geschichtswissenschaften nehmen eine Sonderrolle ein und werden hier ebenfalls ausgeklammert.
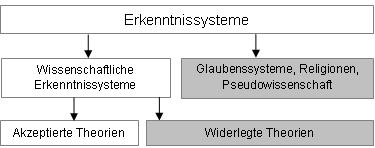
Klassifikation der Erkenntnissysteme
Ingenieurwissenschaften
Die Objekte der Ingenieurwissenschaften sind Artefakte mit Eigenschaften, die an den fertigen Produkten als positiv gegeben wahrgenommen werden. Kühne Hypothesen über das Funktionieren der Gebilde sind nicht erforderlich. Die zur Beherrschung der Technik erforderlichen Kalkulationen mögen kompliziert sein, aber im Grunde genügen Deduktionen im Sinne des Positivismus. Die bewährten naturwissenschaftlichen Gesetze bleiben unhinterfragt. Sie gehören zum (positiven) Bestand des Wissens, ebenso wie die unbezweifelten Regeln der Mathematik und Logik. Diese Art von Positivismus gerät hier nicht in Schwierigkeiten – anders als in den Naturwissenschaften. Das gilt solange, wie eine konsequente Subjekt-Objekt-Trennung möglich ist.
Wenigstens an zwei Stellen kommt es zu Berührungen mit Wissensgebieten, bei denen die positivistische Erkenntnisweise an Grenzen stößt:
- Neue Geräte werden nach Spezifikationen gebaut, die sich am Markt und damit am Bedarf der Gesellschaft orientieren. Erfolg und Misserfolg sind gesellschaftsbedingt. Die Beurteilung technischer Risiken steht unter der Maßgabe persönlicher und gesellschaftlicher Werte und ist damit im Grunde eine Angelegenheit von Ingenieurwissenschaft, Psychologie und Soziologie. Kurz: Risiko ist dreidimensional.
- Entwickler, Konstrukteure und Bediener machen Fehler, jeweils gemessen an der Spezifikation eines technischen Systems. Beim Studium der Denkfallen und der daraus entstehenden kognitiven Täuschungen kommt die Verhaltensforschung ins Spiel. Das betrifft die Biologie, die Psychologie und die Ergonomie.
Aufgrund dieser Berührungspunkte ist eine durchgängige Subjekt-Objekt-Trennung selbst in den technischen Wissenschaften nicht möglich.
Angeregt durch Bassam Tibi – für ihn besteht kein Kontrast zwischen „persönlich“ und „sachlich“ –habe ich in den „Grundlagen des Qualitäts- und Risikomanagements“, 2001, meinen Standpunkt so dargelegt: „Es geht um die Bewertung von Objekten und die daraus folgenden Entscheidungen, aber immer auch um die wertenden und entscheidenden Personen. Die Objektivität liegt darin, dass uns beide Seiten der Medaille bewusst sind – und dass wir beide Seiten zum Gegenstand der kritischen Würdigung machen.“ Ich habe dieses Fachbuch daher auch bewusst im persönlichen Stil formuliert.
Die Ingenieurstätigkeit umfasst auch schöpferische Prozesse, und diese sind genau wie diejenigen in der Kunst wissenschaftlich kaum fassbar. Der fehlende Wissenschaftsanspruch macht das Handeln nicht wertlos. Kritisch wird es nur, wenn Wissenschaftlichkeit zu fordern ist und auch versprochen wird, und wenn dieses Versprechen nicht eingelöst wird.
Naturwissenschaften
Orientierung verschafft uns eine Aussage des Immanuel Kant: „Der Verstand schöpft seine Gesetze … nicht aus der Natur, sondern schreibt sie dieser vor.“ Etwas vorsichtiger formuliert dies Karl Raimund Popper in seinen „Vermutungen“, Kapitel 8.1: „Der Verstand […] versucht, mit mehr oder weniger Erfolg, der Natur die vom ihm erfundenen Gesetze aufzudrängen.“
Genau so funktionieren die empirischen Wissenschaften: Der Forscher stellt kühne und prüfbare Hypothesen auf und macht sich an deren Widerlegung durch genaue Beobachtungen und Experimente. Die Vertrauenswürdigkeit einer Theorie wächst mit der Zahl der strengen Tests, die sie bestanden hat. Das Falsifizierbarkeitskriterium dient der Abgrenzung der Erfahrungswissenschaften von den metaphysischen Erkenntnissystemen: „Ein empirisch-wissenschaftliches System muss an der Erfahrung scheitern können“ (K. R. Popper, Logik der Forschung, 1934, 1982).
Das versuchsweise Aufstellen von Hypothesen, das Formulieren mathematisch-logischer Beziehungen und die Deduktionen bilden den rationalen, rein verstandesmäßigen Anteil am Wissenserwerb. Widerlegungsversuche mithilfe von bereits etablierten Theorien, scharfen Tests und sorgfältigen Beobachtungen machen die kritische Seite aus.
Die Nichtanerkennung einer strengen Falsifizierbarkeit muss nicht notwendig zur Beliebigkeit führen: Thomas Kuhn beschreibt in seinem Buch „The Structure of Scientific Revolutions“ (1962) die Forschung im Rahmen der normalen Wissenschaft als Puzzle-Solving. Neue Paradigmata werden ausgelöst durch die Beobachtung von Anomalitäten. Auch in dieser Epistemologie wird die intersubjektive Prüfbarkeit gefordert, denn allen Beteiligten muss klar sein, wann ein Rätsel als gelöst gilt. Auch über die Einschätzung der Bedeutung von Anomalitäten muss weitgehend Übereinstimmung herrschen.
Geisteswissenschaften
Zwei Merkmale zeichnen die hier zu behandelnden Wissensgebiete aus, nämlich dass
- der Beobachter Teil des Beobachteten wird und dass
- „das Ganze […] sich nur vermöge der Einheit der von seinen Mitgliedern erfüllten Funktionen [erhält]“ (Adorno in „Der Positivismusstreit in der deutschen Soziologie“ von Theodor W. Adorno, Hans Albert, Ralf Dahrendorf, Jürgen Habermas, Harald Pilot, Karl R. Popper, 1969).
Objektivität liegt für Theodor Adorno im „An sich“, also im Wesen der Dinge. Sein Beispiel ist die eben erwähnte Totalität der Gesellschaft. Im Gegensatz dazu steht das „Für uns“, die Erscheinung, der Verstandesgegenstand. Hegel spricht spekulativ und gemäß seiner Dialektik von der Synthese im „An und für sich“ und meint damit eine Art Welt-Geist-Einheit.
Den Erklärungsmustern der hier angewandten Hermeneutik fehlt es an jener Prägnanz, die den Aussagen der Naturwissenschaftler eigen ist. Mir bleibt beispielsweise verborgen, wie das An-sich etwas anderes sein kann als eine durch Sinneseindrücke hervorgerufene Kopfgeburt, also ein Für-uns. Wo soll da ein dialektischer Widerspruch herkommen?
Karl Raimund Popper verlangt in seinem Referat, der zum Positivismusstreit führte, auch von den Sozialwissenschaften die Kritisierbarkeit ihrer Lösungen. Andernfalls müssten sie seiner Meinung nach als unwissenschaftlich ausgeschaltet werden: „Objektivität der Wissenschaft ist nicht eine individuelle Angelegenheit der verschiedenen Wissenschaftler, sondern eine soziale Angelegenheit ihrer gegenseitigen Kritik“.
Ich habe den Eindruck, dass die hermeneutisch-dialektische Erkenntnisweise in vielen heute noch den Geisteswissenschaften zugerechneten Fächern der kritisch-rationalen Erkenntnisweise das Feld überlässt. Es folgen einige Beispiele aus meinen Interessengebieten.
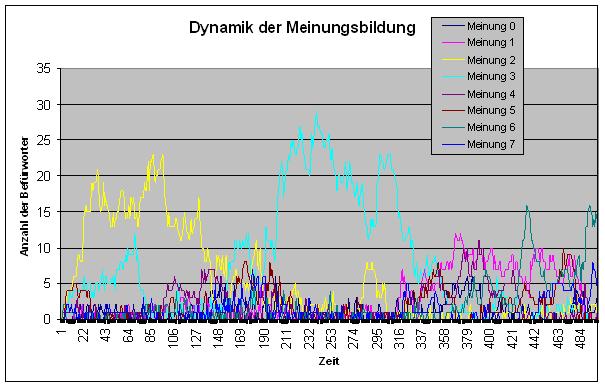
In Philosophie und Psychologie sind die Neurowissenschaften dabei, das Feld zu erobern. Der Soziologie wird stark zugesetzt durch Biologen (Edward Osborne Wilson, „The Social Conquest of Earth“, 2012), Spieltheoretiker (Robert Axelrod, „The Evolution of Cooperation“, 1984) und Physiker (Dirk Helbing, „Social Self-Organization“, 2012). Dass Computersimulationen auf diesen Gebieten eine eigenständige Erklärungskraft entwickeln können, habe ich an meinem (netzöffentlichen) Simulationsprogramm KoopEgo (Kooperation unter Egoisten) erfahren.
Pseudowissenschaften
Alles, was sich als Wissenschaft ausgibt und nicht den Kriterien Prüfbarkeit und Kritisierbarkeit genügt, ist Pseudowissenschaft – ein Glaubenssystem. Von Parawissenschaften wollen wir sprechen, wenn unklar ist, ob Prüfbarkeit gegeben ist oder nicht. Sie nehmen eine Zwischenstellung ein.
Auch im Wissenschaftsbetrieb kommt neuen Ideen zunächst oft nur der Rang von Spekulationen zu. Die Wissenschaft hat schöpferische Räume und Phasen, die unter dem Motto „Anything goes“ (Paul Feyerabend) stehen. Die Frage nach der Prüfbarkeit kommt erst im zweiten Schritt.
Gelingt es auf Dauer nicht, die Prüf- und Kritisierbarkeit und damit die Wissenschaftlichkeit herzustellen, ist das Erkenntnissystem zu verwerfen oder – bei Beharrlichkeit der Befürworter – den Pseudowissenschaften zuzurechnen.
Pseudowissenschaften gehören nicht in den Bildungskanon. Bestenfalls können sie als Schulbeispiele für das kritische Denken herhalten.
Und was ist mit der Mathematik?
Manch einer vermisst unter den aufgelisteten Wissenschaften die Mathematik einschließlich Logik. Dass sie hier nicht als eigenständige Wissenschaft erscheint, liegt daran, dass die Mathematik keine eigenständige Welterklärung liefert. Dabei sehe ich von Vorstellungen ab, in denen beispielsweise die Fünf als heilige Zahl gilt, das aus regelmäßigen Fünfecken zusammengesetzte Dodekaeder für das fünfte, das ätherische Element, steht und das Pentagramm das Symbol der göttlichen Schöpfung und des Lebens ist. Solcherart Zahlenmystik kommt bei den Pseudowissenschaften unter.
Die Mathematik sollte sich, was Weltdeutungen angeht, damit zufrieden geben, Hauptbestandteil des Gebäudes der empirischen Wissenschaften zu sein: „Die wichtigste Funktion der reinen deduktiven Logik ist die eines Organons der Kritik“ (Karl Raimund Popper im Positivismusstreit). Logik und Mathematik zählen zu den Formalwissenschaften; Natur- und die Sozialwissenschaft werden den Realwissenschaften zugerechnet.
Hintergrund
Realität und Repräsentation
Eine schöne Hinführung auf die Auseinandersetzung mit Kants Frage „Was kann ich wissen?“ bietet uns das Bild „Die Hoffräulein“ aus dem Jahr 1656. Eine der viel diskutierten Bildauslegungen ist Einstieg in das Werk „Die Ordnung der Dinge“ von Michel Foucault.
Wir fragen uns, was auf dem Bild eigentlich dargestellt ist. Ist es die Prinzessin, die hell beleuchtet und deutlich sichtbar die Aufmerksamkeit beansprucht? Ist es ein Selbstbildnis des Malers, der – von der Staffelei zurücktretend – prüfend in den Spiegel schaut? Für diese Interpretation spricht auch, wie sich die Blicke der Prinzessin und der rechten der Hofdamen kreuzen. Oder bin ich selbst – der Betrachter – das reale Objekt, das die Blicke der Personen auf sich zieht? Aber dieser Anflug von Realitätsanteilen am Bild verflüchtigt sich in dem Moment, in dem wir im Spiegel an der hinteren Wand das spanische Königspaar als das eigentliche Objekt des Malers Diego Velázquez erkennen.
Der Gedanke einer Realität ist kurz aufgeflackert, aber gleich darauf wieder verlöscht. Was bleibt, ist die pure Repräsentation. Und das gilt nicht nur für die Bildbetrachtung, sondern für alle unsere Erfahrungen. Wir sehen uns in einer Lage, die Immanuel Kant so ausgedrückt hat: „Es sind uns Dinge als außer uns befindliche Gegenstände unserer Sinne gegeben, allein von dem, was sie an sich selbst sein mögen, wissen wir nichts, sondern kennen nur ihre Erscheinungen.“
Elimination der Weltanschauung
Wir verzichten auf die Klärung der Frage, was Realität ist und was sie auszeichnet. Für den Zweck der Abgrenzung der Wissenschaft ist die Klärung dieser Fragen glücklicherweise von untergeordneter Bedeutung. Durch den Verzicht darauf, das Wesen der Dinge zu ergründen, wird der in diesem Weblogbuch verfolgte Bewertungsansatz für Vertreter unterschiedlicher Weltanschauungen akzeptabel – so hoffe ich zumindest.
Orientierung bietet die evolutionäre Erkenntnistheorie von Gerhard Vollmer, die an den kritischen Rationalismus von Karl Raimund Popper anschließt. Diese Epistemologie wird mehr oder weniger fest mit einer naturalistische Ontologie verbunden. Letztere wurde von Mario Bunge und Martin Mahner präzisiert. Diese Ontologie geht vom Vorhandensein einer vom Bewusstsein unabhängigen Realität und von einigen Postulaten wie dem Kausalitätsprinzip aus. Danach ist es Aufgabe der Wissenschaft, mit ihren Theorien dieser objektiven Realität möglichst nahe zu kommen.
Für den hier verfolgten Zweck einer Abgrenzung dessen, was als Wissenschaft gelten soll und was nicht, ist eine Bezugnahme auf diese Ontologie – wie bereits angedeutet – entbehrlich. Selbst der bekennende Realist Popper sieht das so: „Die Idee […] der Annäherung an die Wahrheit, spielt in der Logik der Forschung eine wichtige Rolle, obwohl die in diesem Buch entwickelte Theorie an keiner Stelle von dieser Idee abhängt.“ (Logik der Forschung Anhang *XV. Über Wahrheitsnähe)
Wie die Mathematiker ihre Sätze jeweils aus einer möglichst geringen Zahl von Axiomen ableiten, so wollen wir von möglichst wenigen Grundannahmen ausgehen. Von wissenschaftlichen Aussagen wollen wir im Grunde nur deren Prüfbarkeit verlangen. Und damit kann der Atheist und Materialist, der Agnostiker und beispielsweise auch ein Sektenbeauftragter der katholischen Kirche einverstanden sein.
Wenn wir verschiedene Ontologien – ohne uns darauf zu beziehen – zulassen, müssen wir darauf gefasst sein, dass es zu unterschiedlichen Zuordnungen kommt. Das bleibt jedoch glücklicherweise ohne schwerwiegende Folgen.
Mit dem Verzicht auf ontologische Begründung geht auch der Wahrheitsbegriff und damit die Möglichkeit einer zeitunabhängigen Bewertung der Wahrheitsnähe von Erkenntnissen verloren. Es ist dann kaum möglich, der Homöopathie beispielsweise von Anfang an den Stempel „Pseudowissenschaft“ aufzudrücken, denn es handelt sich ja tatsächlich um ein prüfbares Heilverfahren. Demgegenüber sieht Mahner in der Homöopathie eine Pseudowissenschaft: Sie beruht seiner Meinung nach auf Illusion und auf Annahmen, die mit der naturalistischen Ontologie nicht vereinbar sind.
Letztlich kommen die Vertreter unterschiedlicher Ontologien doch wieder zusammen. Um beim Beispiel der Homöopathie zu bleiben: Sie hat die vielen ihr auferlegten Prüfungen nicht bestanden. Sie gilt inzwischen als mehrfach widerlegt. Die heutigen Vertreter der Homöopathie arbeiten mit Behauptungen, die sich jeglicher Kritik entziehen. Sie betreiben – so oder so gesehen – Pseudowissenschaft.
Noch eine Warnung zum Schluss: Ontologien können zur Fortgschrittsbremse werden. Wer das Wesen der Dinge zu kennen meint, wird blind für Neues. Das wissen wir aus Zeiten, als die Religion noch eng mit der Wissenschaft verwoben war. Aber auch heute ist die Gefahr nicht vollständig gebannt. Der Naturalist beispielsweise läuft Gefahr, fruchtbare Spinnereien voreilig abzuwürgen und so den Spielraum für schöpferisches Tun einzuschränken: Früher galt der Äther – das Feinstoffliche, das fünfte Element – als Träger der Lichtwellen. Für diesen (illusorischen) Äther formulierte James Clerk Maxwell die elektromagnetische Theorie. Durch Einsteins Relativitätstheorie wurde die Ätherhypothese widerlegt. Der Kern der maxwellschen Theorie aber hat überlebt und für grundlegende Veränderungen unseres Lebens gesorgt.