Kettenbrüche oder Kettenwurzeln sind für den Mathematiker kein Problem, solange sie endlich sind. Zur Berechnung beginnt man hinten bzw. rechts unten und arbeitet sich Schritt für Schritt bis zum Anfang vor. Die unendlichen Kettenausdrücke machen es einem nicht so einfach. Wo beginnen?
Wenn der unendliche Kettenausdruck sukzessive durch eine Folge endlicher Kettenausdrücke gewonnen worden ist, haben wir ein Rezept: Wir können die Folgenglieder dem Kettenausdruck entnehmen und ihren Grenzwert berechnen. Das einzig Bemerkenswerte an unendlichen Kettenbrüchen ist, soweit ich sehen kann, ihre Unhandlichkeit. Meistens gibt es elegante Lösungswege, die an ihnen vorbeiführen.
Schauen wir uns den unendlichen Kettenbruch des folgenden Bildes an: 1+1/(2+1/(2+1/(2+…))). Den gesamten Ausdruck setzen wir gleich x und den Bruch gleich u. Es ist x=1+u und u = 1/(2+u). Dabei nutzen wir aus, dass auf der ersten (tiefgestellten) Schachtelungsebene genau derselbe Bruch steht, wie ganz oben. Daraus folgt 1=(x-1)(x+1) = x2-1. Also: x = √(2). Für die Berechnung der Wurzel aus 2 haben wir nun wirklich effizientere Verfahren als dieses Ungetüm von Kettenbruch, beispielsweise das Newton-Verfahren (babylonisches Wurzelziehen).
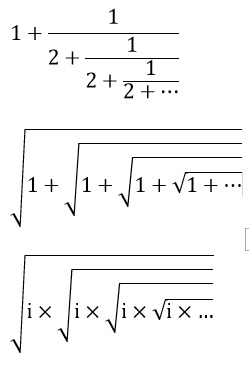
Schlimmer noch scheinen mir die Kettenwurzeln zu sein. Aber es gibt Liebhaber dieser Konstruktionen. Nehmen wir die im Bild dargestellte unendliche Kettenwurzel √(1+√(1+√(1+…))).
Ich will mich nicht damit aufhalten, diese zur Folge aufzudröseln. Ich setze voraus, dass die Folge gegen einen Grenzwert x konvergiert. Dann kann man schreiben: x = √(1 + x). Quadrieren und alles auf die linke Seite bringen ergibt: x2–x-1=0. Die Lösung x dieser Gleichung ist gleich dem Streckenverhältnis des goldenen Schnitts. Dank dieser Entdeckung hüpft das Herz des Zahlenmystikers vor Freude! Weiterlesen